Fısıltı Odasının Sırrı Nedir?
Matematikçi ve mimar Sir Christopher Wren tarafından 17. yüzyılda tasarlanmış bir oda, fısıltı odası olarak adlandırılıyor. Londra’daki St. Paul Katedrali’ndeki bu odada, birbirine uzak iki noktada, sırtları birbirine dönük duran iki kişi sadece fısıldaşarak iletişim kurabiliyor. Ne kadar gizemli görünse de odanın niçin böyle olduğunu anlamak için biraz matematik bilmek yeterli.

Reezky Pradata/ iStock.com
Bir arkadaşınızla uzun bir odanın içine girdiğinizi ve odanın iki tarafına giderek birbirinize sırtınızı döndüğünüzü gözünüzde canlandırın. Arkadaşınızın fısıldadığınız her kelimeyi duyabilmesi için sizce odanın şekli nasıl olmalıdır? Ayrıca siz ve arkadaşınız bunun için odanın hangi noktalarında durmalısınız? İlk bakışta çok zor görünen bu sorunun basit cevabı için birazcık matematik bilmek yeterli.
Fısıldadığınız kelimeleri arkadaşınızın duyabilmesi için odanın duvarlarından yansıyan ses dalgalarının arkadaşınızın kulağına doğru yönelmesi gerekir. Bunun gerçekleşmesi için odanın elips şeklinde olması, sizin ve arkadaşınızın da elipsin odak noktalarında durması yeterlidir.
Günlük hayatta pencere, köprü kemerleri ve merdiven gibi pek çok mimari alanda elips eğrisine rastlamak mümkündür. Dünya’nın Güneş’in etrafında dolanışı sırasında izlediği yol ve bir spor aleti olan eliptik bisiklette ayaklarınızın hareketi de yine elips şeklindedir.
Peki elips şeklini özel kılan ne?
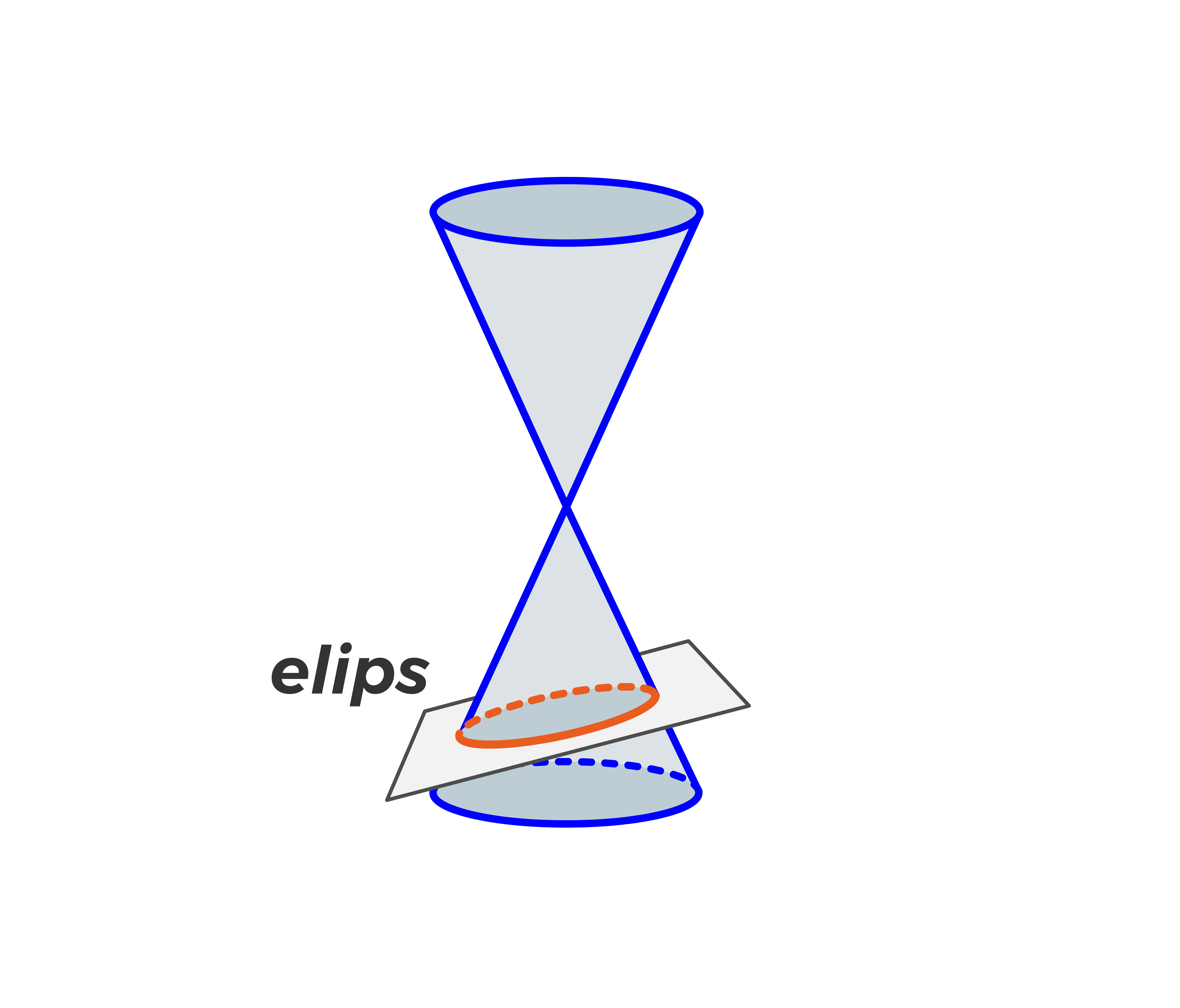
Elips geometrik şekli aslında bir koni kesitidir. Üç boyutlu katı bir cisim olan koni ile bir düzlemin kesişim eğrisidir. Matematiksel olarak elips, odak noktalarına uzaklıklarının toplamı sabit olan noktalar kümesidir.
Elipsin iki adet odak noktası bulunur. Bu noktalar, elipsin içerisinde, uzun eksen üzerinde ve elipsin merkezinden belirli bir uzaklıkta yer alır. Bir elips çizmenin basit yollarından biri, bir düzleme birbirine iple bağlı iki iğne batırıp ipi bir kalemle gerdirerek iğnelerin etrafından kapalı bir eğri çizmektir.
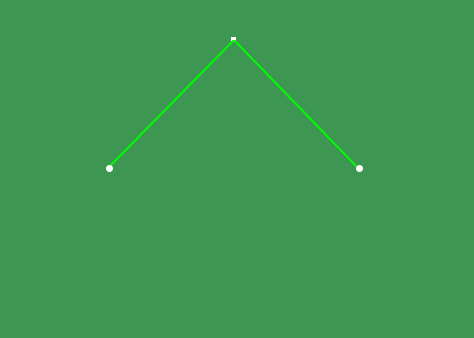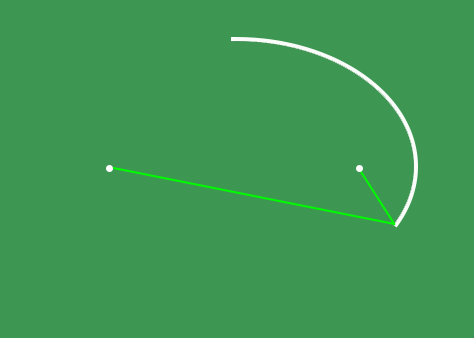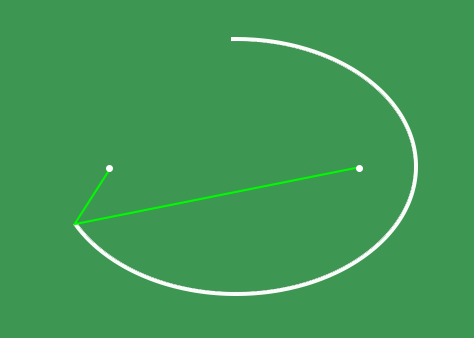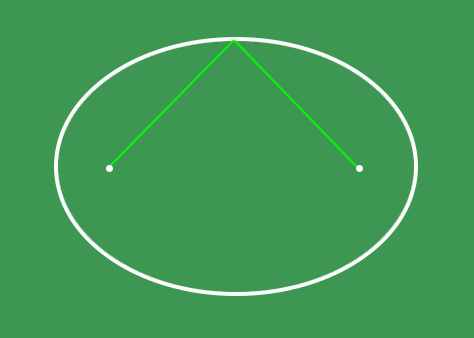
Düzleme batırdığımız iğneler elipsin odak noktalarıdır. Çizme işlemi sırasında ipin gergin kalması, elips üzerindeki noktaların odak noktalarına uzaklıkları toplamının sabit kalmasını sağlar.
Merkezinin koordinatları (h, k) olan bir elipsin genel denklemi
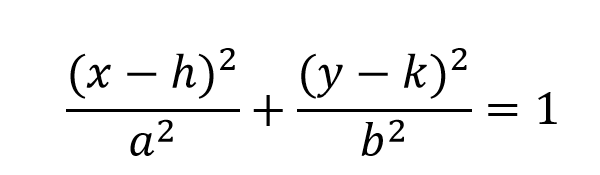
şeklindedir. Bu eşitlikteki ‘a’ değeri elipsin uzun ekseninin uzunluğunun, ‘b’ değeri ise elipsin kısa ekseninin uzunluğunun yarısıdır. Elipsin odak noktaları ise
koordinatlarında yer alır.
Fısıltı odasındaki sırrın elipsin yansıtıcı özelliğine dayandığını artık biliyoruz. Öyleyse yansımanın nasıl gerçekleştiğine de bakalım:
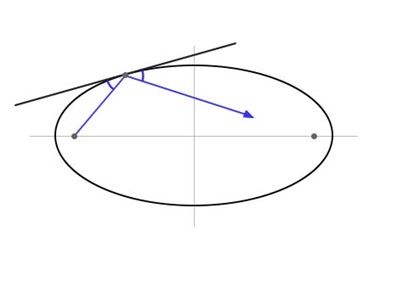
Elips şeklinde bir yüzeyinizin ve elipsin kenarları boyunca da bir aynalı yüzeyinizin olduğunu varsayalım. Elipsin odak noktalarından birinden çıkan bir ışın, elips üzerinde bir nokta ile karşılaştığında yansır. Işının elips üzerindeki bir noktadan yansıması aslında o noktanın teğet doğrusundan yansımasıdır. Teğet ile gelen ışın arasındaki açı her zaman teğet ile yansıyan ışın arasındaki açıya eşittir. Böylece bir odak noktasından çıkan ışın, yansıyarak diğer odak noktasına ulaşır. Fısıltı odasının sırrı da, ses dalgalarının yayılımını da etkileyen bu elips şeklindeki yapısına dayanmaktadır.
Kaynaklar:
- https://personal.math.ubc.ca/~cass/courses/m309-01a/dawson/index.html
- https://www.stpaulscathedral.uk/the-whispering-gallery