GeoGebra ile Konik Cisimlerin Kesitleri

Üç boyutlu şekillerden biri olan koni cismi sizin için ne ifade ediyor, bu şekli nasıl tanımlarsınız? Etrafımızdaki nesnelerden koniye örnek verebileceğiniz neler var? Bir dondurma külahı bir koni olabilir mi? Siz bunları düşünürken çoğumuzun bugüne kadar karşısına çıkmış bir problem olan koni üzerinde yürüyen karıncayı ele alalım. Bir koni hayal edelim ve koni üzerinde bir karınca olsun ve yürümeye başlasın. Sizce bu karınca koni üzerinde nasıl bir yol izleyebilir? Taban çevresinde dolaştığında hangi uzunlukta gitmiş olur? Tepe noktasına giderken hangi yolu izlemelidir? Başladığı noktaya en kısa yoldan tekrar nasıl ulaşabilir?

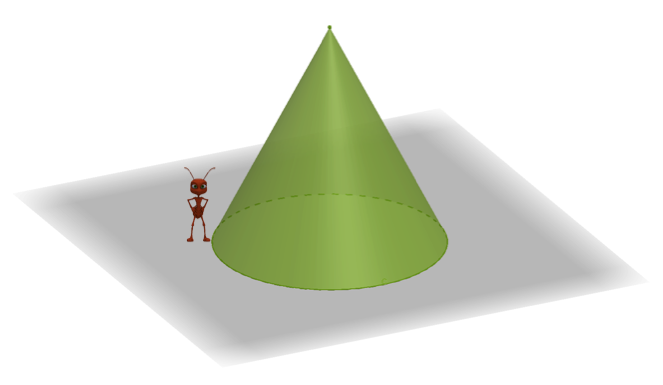
Bu soruların hepsini koninin özelliklerini ve açılımını hayal etmeden ve bilmeden cevaplamamız hayli zor. Bu yüzden öncelikle koni hakkında bilgi verip daha sonra koni ve özelliklerini GeoGebra programını kullanarak keşfetmeye çalışalım. Koni, “bir düzlem içindeki dairenin her noktasını, düzlem dışındaki bir noktaya birleştiren doğru parçalarının meydana getirdiği geometrik şekil” olarak tanımlanır. Bu tanımdan anlaşılacağı gibi koni üç boyutlu bir katı cisimdir.

Koni dik üçgenin bir dik kenarı etrafında döndürülmesiyle elde edilir. Bu koniye dik koni veya dönel koni denir. Bir üçgenin yüksekliği etrafında döndürülmesiyle de bir koni oluşur. Koniler tabanlarına göre dairesel koni, eliptik koni gibi isimler alır. Dairesel bir dik koninin taban merkezini tepe noktasına birleştiren doğru parçasına bu koninin ekseni veya yüksekliği denir. Taban çevresinin herhangi bir noktasını tepe noktasına birleştiren doğru parçasına koninin ana doğrusu adı verilir. Taban çevresinin her noktasını tepe noktasına birleştiren doğru parçalarının meydana getirdiği yüzeye ise koninin yanal yüzeyi denir.

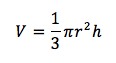
Bir dönel koninin düzlemlerle arakesitine konikler adı verilir. Herhangi bir koni tabana paralel bir düzlem ile kesilirse, düzlemle taban arasında kalan kısma kesik koni denir. Örneğin bu koniyi bir düzlemle kesersek ve karınca kesilmiş koninin yüzeyinde yürürse nasıl bir yol izler? Bulunduğu noktaya olan en kısa uzaklığı değişir mi? Bu soruları da GeoGebra programını kullanarak cevaplamaya çalışalım.

Şimdi, bir koniyle bir düzlemin arakesitini düşünelim. Sizce arakesitler hangi geometrik şekilleri oluşturur? Kesiştirdiğimiz düzlemin koninin tabanına paralel olup olmaması arakesiti değiştirir mi? Örneğin koni herhangi bir yükseklikten kesilmiş olsun. Karınca A noktasından yürümeye başlasın. Koninin açılımını A noktasından kestiğimizi düşünelim. A ve B noktaları olarak iki nokta elde edelim. Bu durumda en kısa yol [AB] doğru parçası olacaktır. Eğer kestiğimiz yükseklik, açılımda [AB] doğru parçasının üstünde kalacak şekildeyse karıncanın yolu değişmez ancak yükseklik azaldıkça karıncanın kesilmiş yüzeyden yürümesi gerekecektir. Şimdi Şekil 1’deki etkinliği inceleyelim.

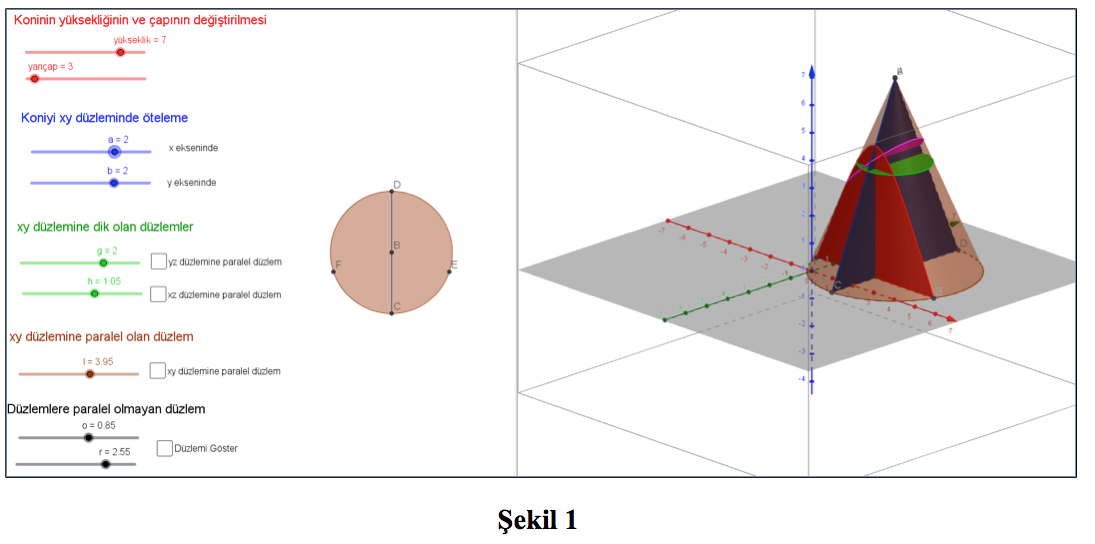
Şekil 2’deki sürgüleri dinamik olarak hareket ettirerek yükseklik, yarıçap gibi değişkenleri istediğimiz uzunlukta ayarlayabiliriz. Aynı zamanda koninin konumunu da ilgili sürgüler yardımıyla öteleyebiliriz. Bu da bize koninin dinamik yapısını görmemize ve birçok koni çeşidini incelememize imkân sağlar.

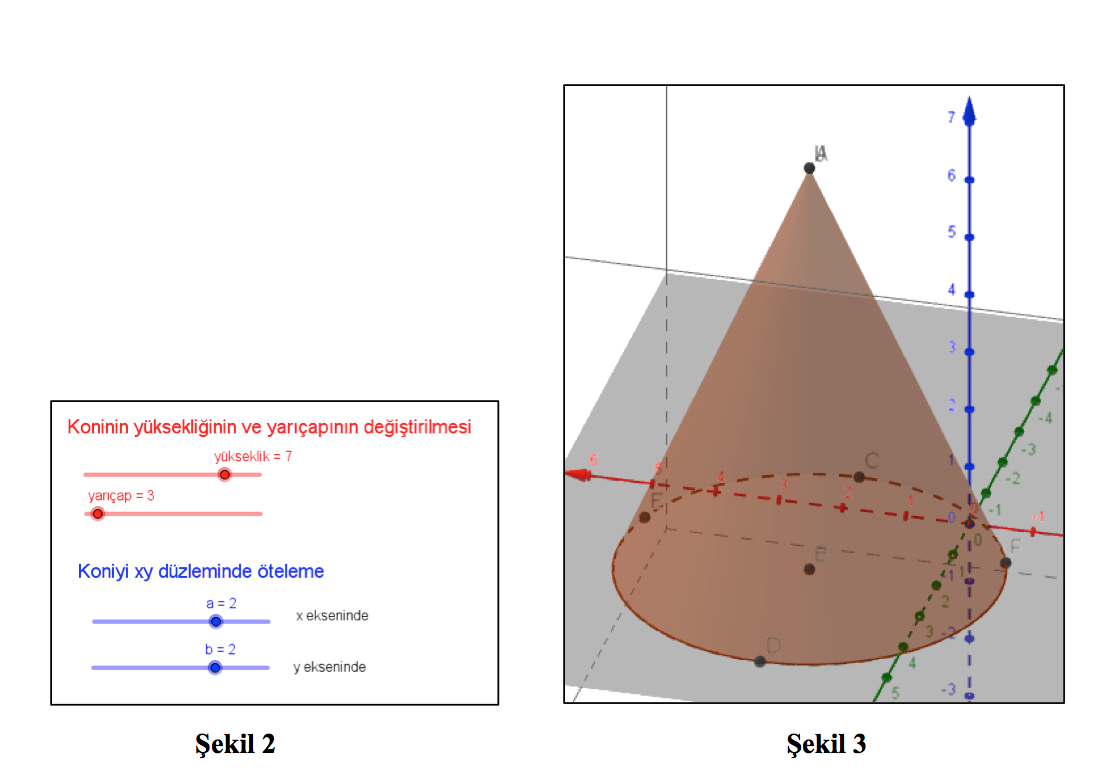
Ayrıca sürgüye bağlı olarak oluşturulan koni (Şekil 3) komutlarla değiştirilebilir ve ötelenebilir. Dolayısıyla koninin konumunu değiştirerek düzlemde farklı koniler elde etmiş oluruz. Örneğin (2,2,7) noktası koninin tepe noktasıdır. Yükseklik sürgümüzü 7’den 3’e getirdiğimiz zaman tepe noktamız (2,2,3) olacaktır. Yani yükseklik 7 birimden 3 birime düşmüş olacaktır.

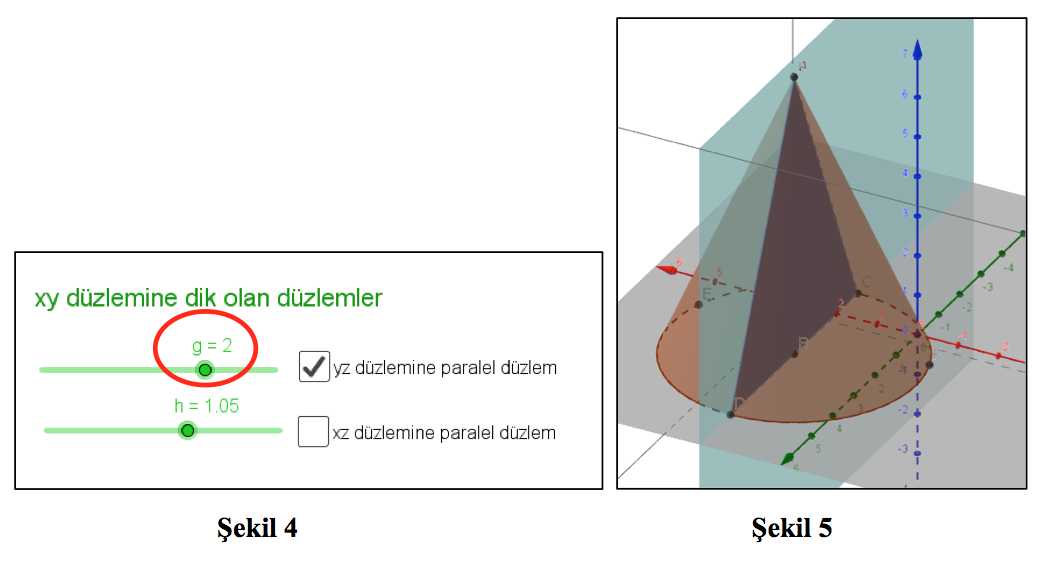
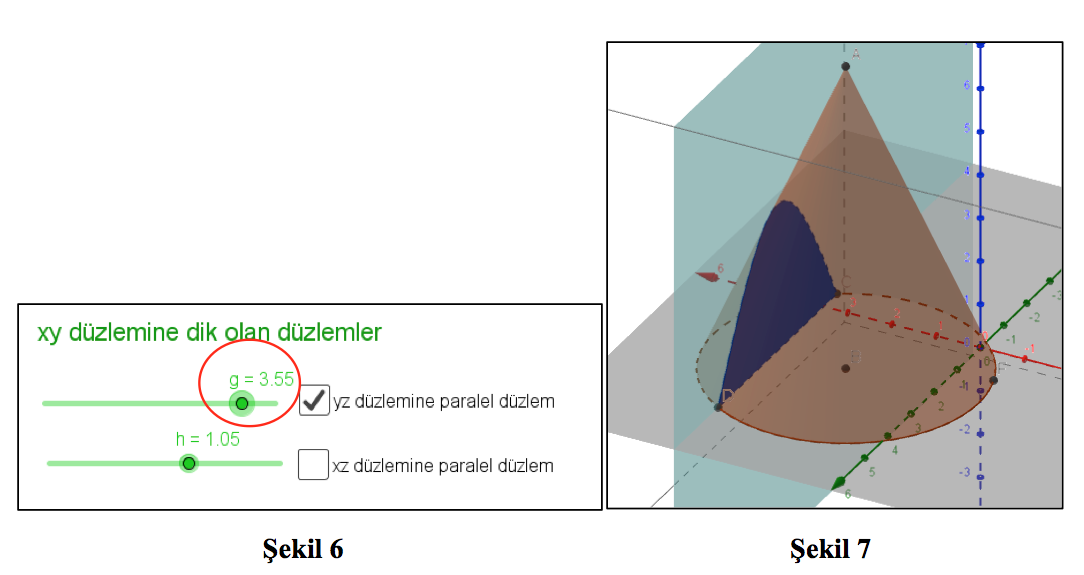
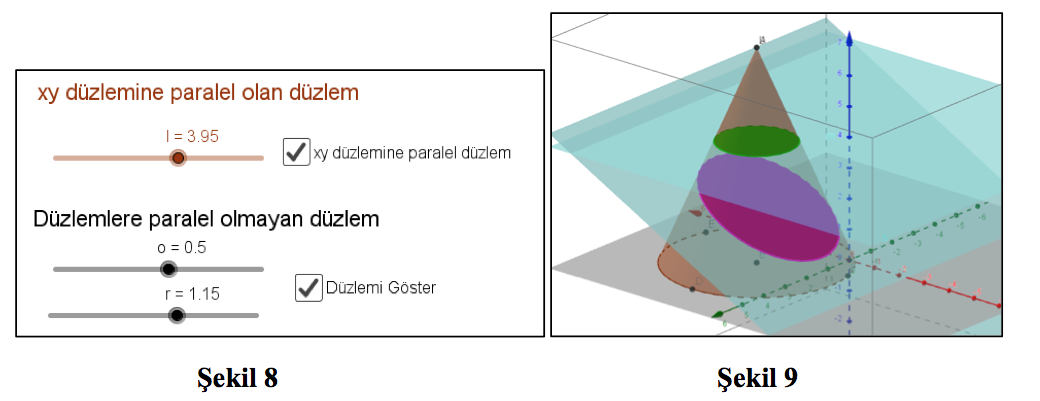
Gösterilmesini istediğimiz düzlemi, yanında bulunan kutucuk yardımıyla açıp kapatabiliriz. Düzlemi koni ile kesiştirebilir ve sürgü yardımıyla düzlemi değiştirebiliriz. Örneğin g sürgüsünü 2’den 3,55’e yükselttiğimizde Şekil 5’ten Şekil 7’yi elde etmiş oluruz. Arakesit bir üçgen iken bir hiperbole dönüşmüş olur (Şekil 7).

Koninin tabanına paralel olan düzlemi açtığımız zaman arakesitinden bir daire elde ederiz. Paralel olmayan düzlemden ise bir elips elde ederiz (Şekil 9). Bu daire ve elipsi de sürgüler yardımıyla değiştirebiliriz (Şekil 8).

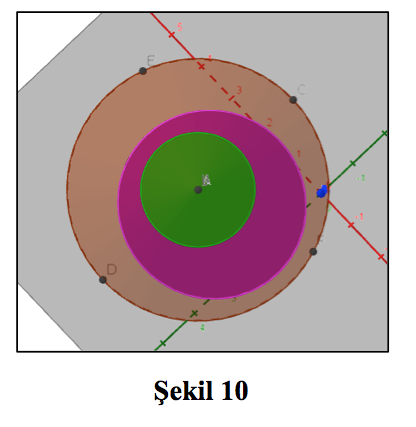
Arakesitlerin izdüşümünü görmek istersek koniye tepeden bakmak için üç boyutlu ortamda koniyi çevirebiliriz. Bunu yapmak için koniyi tutup istediğimiz yönde döndürebiliriz. Bu, bize koniye her açıdan bakabilme imkânı sağlayacak ve zihnimizde canlandıramadığımız nesneleri somutlaştırmamıza yardımcı olacaktır (Şekil 10).

Bu şekilde oluşan arakesitleri görsel olarak öğrenmek, uzay geometri konusunun hayal edilebilmesini ve konunun akılda kalmasını kolaylaştıracaktır. Düzlemlerin birbirlerine göre durumları ve aralarındaki açılar bu yazılım ile incelenebilir. Sadece koni ile değil tüm katı cisimler için bu etkinliğe benzer etkinlikler tasarlayabiliriz. Bu etkinliğin nasıl inşa edileceği https://www.youtube.com/watch?v=jTJIWgsTCmU bağlantı adresinde ayrıntılı bir biçimde anlatılmıştır. Diğer katı cisimlerin inşasını siz sevgili okuyucularımıza bırakıyoruz.