Ortalama Sürat (Hız Değil!) Kolayca Nasıl Hesaplanır?

Sayılarla başlayan yazı serüvenimiz aynı “süratle” devam ediyor. Fen bilimleri ile ilgilenen arkadaşlarımın son zamanlardaki uyarıları sayesinde hız yerine sürat denilmesi gerektiğini öğrendim. Çünkü hız vektörel (yönlü), sürat ise skaler (yönsüz) bir büyüklüğü gösteriyormuş. Benzer bir durum üniversite sınavlarında sıkça karşılaşılan “işçi-havuz problemleri”nin adlandırılmasında da var. Bu problemlerle karşılaştığımda hep şöyle söylenirim: “Arkadaşım, bizim işçi kardeşimizle ya da havuzla bir problemimiz yok, bizim sorunumuz iş ve işin bitirilmesi”. Tabii bunu söyleyince yüzlerde gülümseme eksik olmaz. Hız problemlerinin de iş problemleri ile aynı kaderi paylaştığını öğrendiğime göre bundan sonra matematik dersinde hız problemlerine sürat problemleri demek gerektiğini yüksek sesle belirteyim.

Matematikte ortalamalar; sayılarla yapılan işlemler, istatistik ve çıkarımda bulunma açısından çok önemlidir. Ortalamaların en çok kullanılanları arasında aritmetik ortalama (A.O), geometrik ortalama (G.O) ve harmonik ortalama (H.O) sayılabilir. Bu ortalamalar aşağıdaki şekilde tanımlanır.

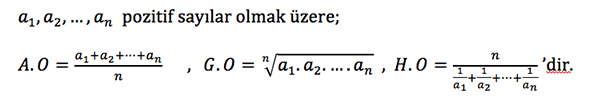
Bilimde en çok kullanılan ortalama hesabının iki toplamsal ifadenin oranı olduğunu söyleyebiliriz. Örneğin sürat ve ortalama sürat;

olarak hesaplanır. Bu noktada matematiksel bir kolaylığı kullanarak benzer ortalama hesaplamalarını daha hızlı yapabilirsiniz. Peki, nasıl? Örneklerle açıklayalım.

Eğer (toplam X) bölü (toplam Y) şeklinde bir ortalama 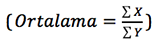 hesaplıyorsanız (ki ortalama sürat ya da ortalama yoğunluk hesaplarken tam da bunu yapıyoruz!) işte size matematiksel kolaylık.

1. Durum: 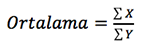   şeklinde bir hesaplama yaparken payda (Y’ler) kısmındaki tüm veriler eşitse aritmetik ortalama kullanılabilir.

Örnek: Sabit süratle hareket eden bir araç AB, BC ve CD arasını dörder saat süreyle almaktadır. A, B ve C şehirlerinden sırasıyla 70 km/sa, 20 km/sa ve 90 km/sa hızla hareket eden bu aracın AD yani tüm yol boyunca ortalama sürati kaçtır?

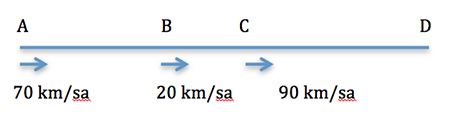
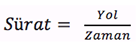 olarak hesaplanırken bu soruda alınan yollardaki süreler (paydalar) eşit olduğundan ortalama sürati bulmak için aritmetik ortalama kullanılabilir.

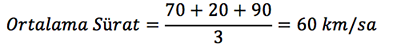
Peki, bu hesap nereden geliyor? Şimdi, n tane aracımızın süratleri 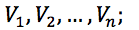aldıkları yollar  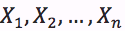olmak üzere her biri aynı/eşit  t  sürede yol alsın.

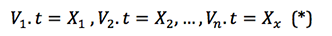
olarak yazılabilir.

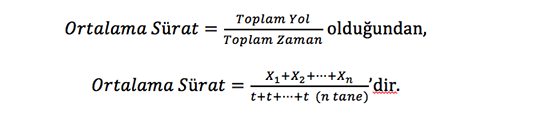
Dolayısıyla (*) eşitliği kullanılarak,

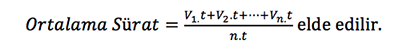
Pay kısmı ortak t parantezine alınırsa,

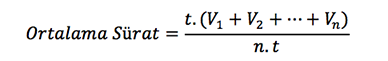
t’ler sadeleştiğinde,

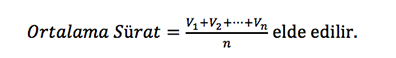
Böylece paydalar (yani süreler) eşit olduğunda ortalama sürati bulmak için aritmetik ortalama kullandığımız ortaya çıkar.

2. Durum: 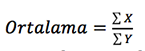   şeklinde bir hesaplama yaparken paylar (X’ler) kısmındaki tüm veriler eşitse harmonik ortalama kullanılabilir. Örneğimizi başka bir ortalamada kullanalım, mesela sıvıların yoğunluğunu hesaplarken.

Örnek: Dört farklı sıvının yoğunlukları sırasıyla 2, 3, 4 ve 6 g/cm³ olarak veriliyor. Bu sıvılardan eşit kütlede alınarak sıvılar birbiriyle karıştırıldığında elde edilen karışımın yoğunluğu ne olur?

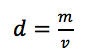 ve burada sıvıların kütleleri eşit (paylar eşit) olduğundan harmonik ortalama kullanabiliriz.

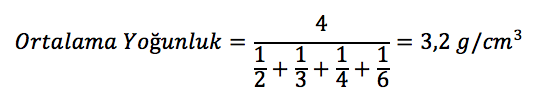
Böylece bu tür ortalamaları -örneğin ortalama sürat, ortalama yoğunluk- hesaplarken daha kısa ve çabuk bir yöntem kullanmış oluruz. Aşağıdaki soru sizin için!

Son örnekte verdiğimiz durumun ispatı nasıl yapılır? Yani kütleler (paylar) eşitse harmonik ortalama neden kullanılır? İspatını yapabilir misiniz?

Not: İspatın doğruluğu için burak.karabey@deu.edu.tr adresine e-posta gönderebilirsiniz.