Yüzey Döşemeleri

Özdeş geometrik şekiller kullanarak yüzeyleri döşemek, çok eski zamanlardan beri insanların zihnini meşgul eden matematik problemlerinden biri. Bu amaçla kullanılabilecek çeşitli şekiller biliniyor. 1918 yılında Karl Reinhardt yüzey döşemesi olarak kullanılabilecek tüm geometrik şekillerin bulunması ve listelenmesi konusunda bir çalışma başlattı. Aradan geçen zamanda amatörler de dâhil olmak üzere pek çok matematikçi bu konu üzerinde çalıştı. En son 2015 yılında 30 yıl aradan sonra yeni bir beşgen keşfedildi. Ancak listenin tamamlanıp tamamlanmadığı, başka bir deyişle hâlâ yeni geometrik şekiller keşfetmenin mümkün olup olmadığı bilinmiyordu. Michaël Rao, arXiv’e yüklediği bir makalede mümkün olan tüm geometrik şekillerin keşfedildiğini gösterdi.

Üçgen Yüzey Döşemeleri

Herhangi bir üçgenle yüzey döşemek mümkündür (bkz. aşağıdaki şekiller).

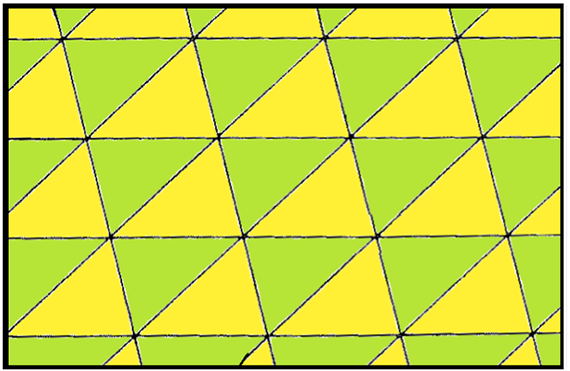
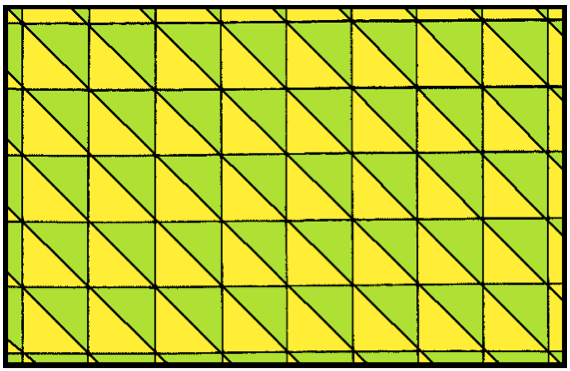
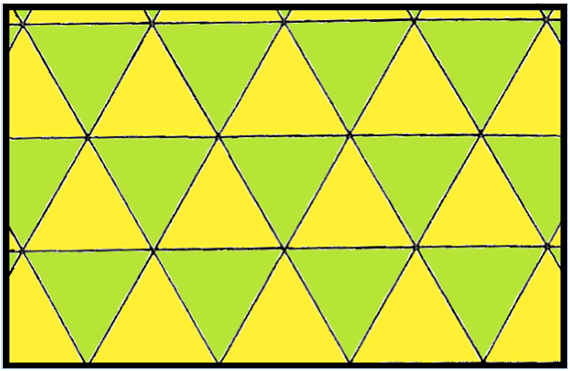
Wikipedia

Dörtgen Yüzey Döşemeleri

Üçgenlerde olduğu gibi herhangi bir dörtgenle de yüzeyleri döşemek mümkündür (bkz. aşağıdaki şekiller).

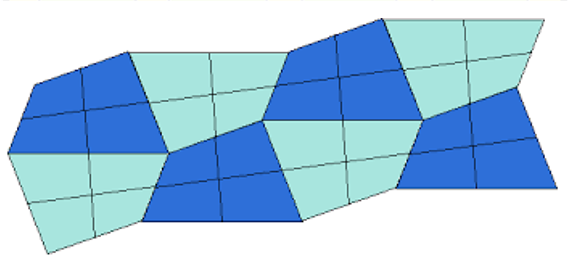
http://www.tonibest.com/cdn/6/2002/430/

Altıgen Yüzey Döşemeleri

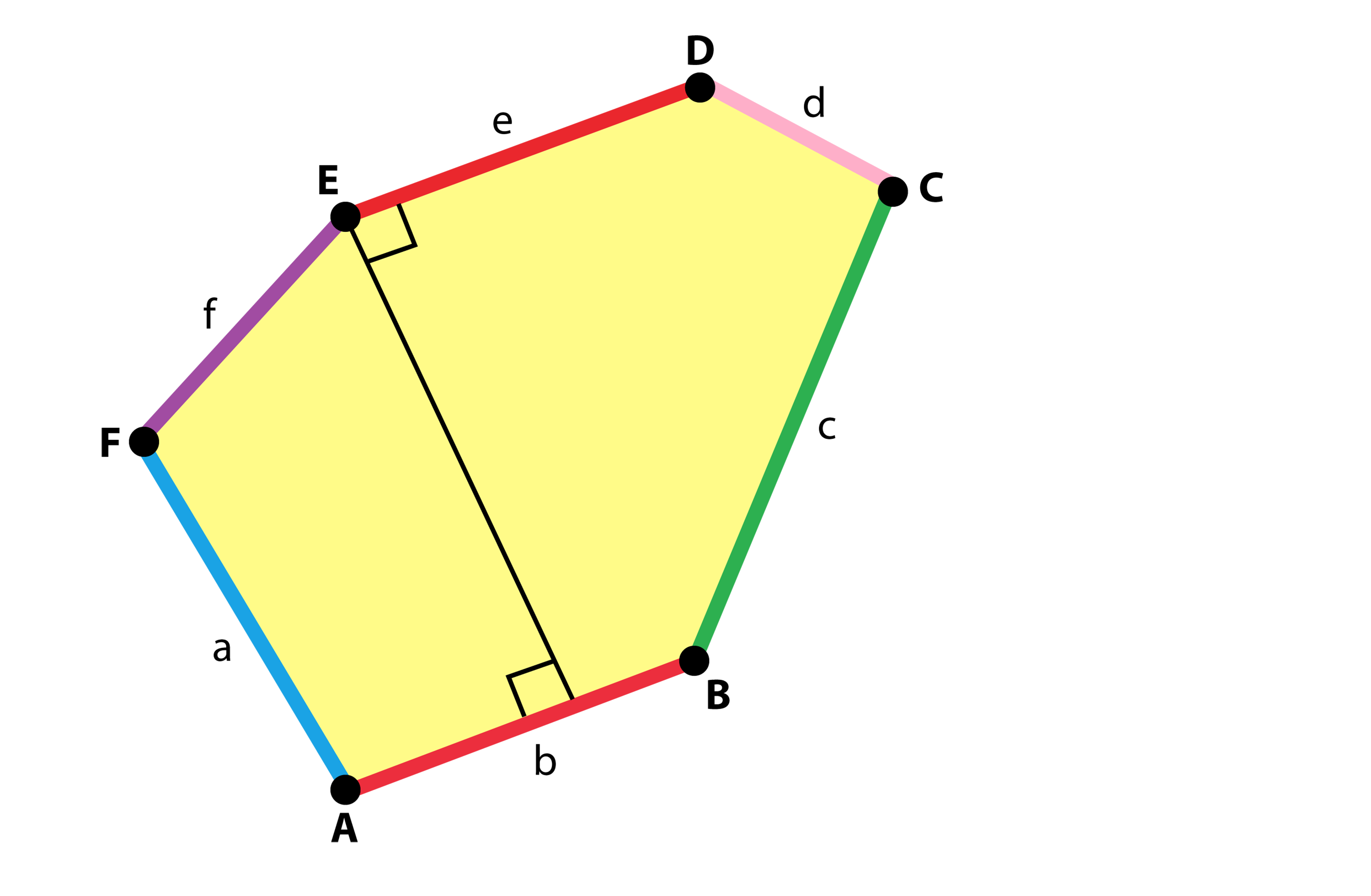
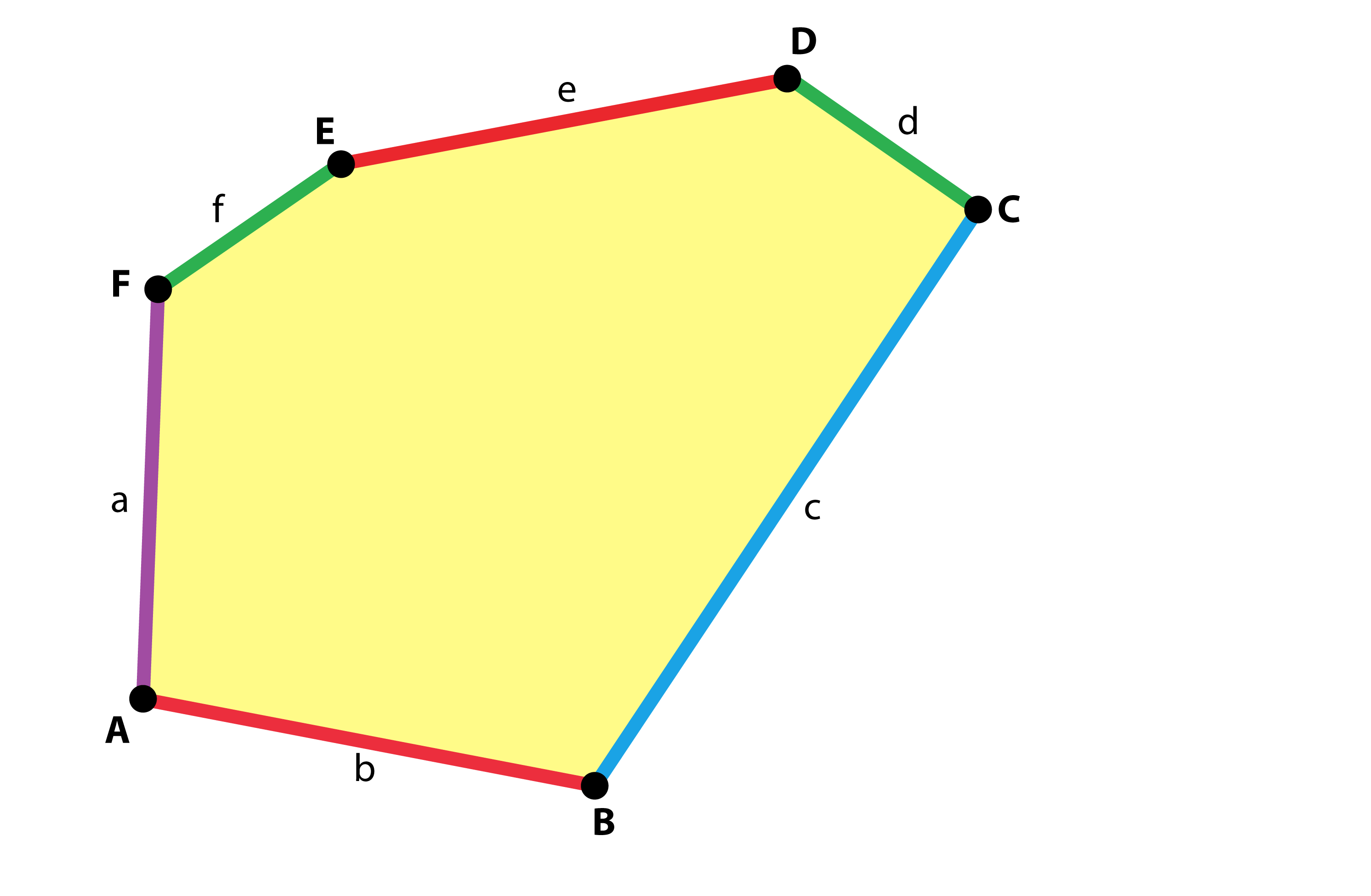
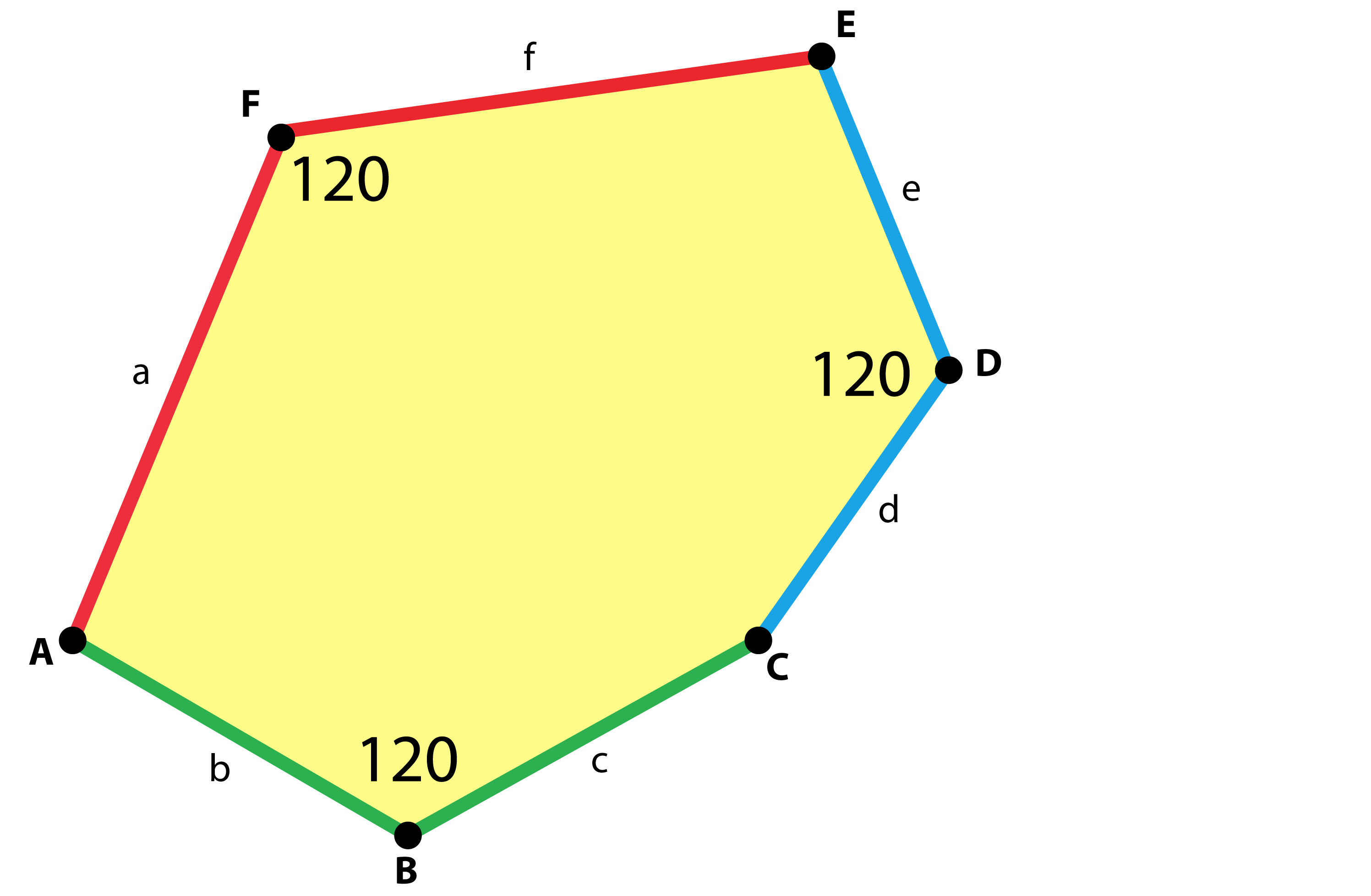
Üçgenlerin ve dörtgenlerin aksine herhangi bir altıgenle bir yüzeyi döşemek mümkün değildir. Bir yüzeyi hiç boşluk bırakmaksızın kaplayabilecek üç tür altıgen olduğu biliniyor.

b=e, B+C+D=360°

b=e, d=f, B+C+E=360°

a=f, b=c, d=e, B=D=F=120°

Düzgün altıgen yukarıdaki türün tüm kenarları birbirine eşit olan özel bir durumudur.

Yedigen ve Daha Büyük Çokgenler

Yedigenlerle ve daha büyük çokgenlerle bir yüzeyi döşemek mümkün değildir.

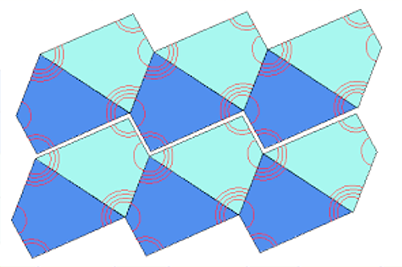
Beşgenler

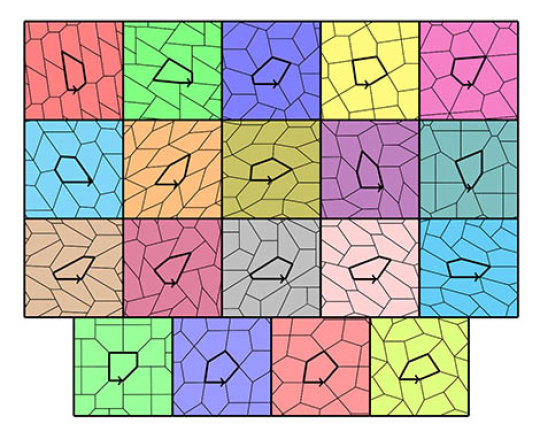
Yüzey döşemeleri konusunda matematikçilerin zihnini en çok meşgul eden çokgenlerin beşgenler olduğu söylenebilir. Düzgün beşgenlerle (tüm kenarları aynı uzunlukta beşgenlerle) hiç boşluk bırakmaksızın bir yüzeyi kaplamak imkânsızdır. Ancak düzgün olmayan beşgenlerle mümkündür. 1918-2015 arasında 15 ayrı tür beşgenin bu amaçla kullanılabileceği bulunmuştu. Ancak gelecekte başka tür beşgenlerin de keşfedilmesinin mümkün olup olmadığı bilinmiyordu.

Michaël Rao ilk olarak bir yazılım yardımıyla tüm olasılıkları taramış ve 371 tür beşgenin yüzey döşemesi olarak kullanılabilecek potansiyele sahip olduğunu görmüş. Daha sonra bu beşgen türlerinin tamamını tek tek test etmiş ve sadece 19’unun gerekli tüm koşulları sağladığını belirlemiş. Bu 19 türün 15’i daha önceden de bilinenler. Geriye kalan 4 türse sadece diğer 15 türün özel durumları (bkz. aşağıdaki şekil). Dolayısıyla Rao’nun çalışmaları bugün yüzey döşemesi olarak kullanılabilecek tüm beşgen türlerinin ve dolayısıyla tüm çokgen türlerinin zaten bilindiğini ve gelecekte yeni türlerin keşfedilemeyeceğini gösteriyor. Böylece yüz yıldır matematikçilerin zihnini meşgul eden bir soru da cevaplanmış oluyor.