Düşündüren Matematik: √7 (Karekök Yedi) Nerede?

Sayılarla uğraşmak zorlu ve sabır gerektiren bir süreçtir. Bu konuyla ilgili en güzel deneyimim sayı doğrusu üzerinde sayıları bulmaya çalışmak olmuştur. Bu noktada, matematikte kendi kendime yeni bir keşif yaptığımı söyleyebilirim. O da “birim” meselesiyle ilgilidir. Matematiği diğer bilimlerden ayıran ve matematiğin kafamızın içinde delice dolaşmasını sağlayan şey, herhangi bir “birim” ile çalışma zorunluluğu olmamasıdır. Örneğin sayı doğrusu üzerine sayıları yerleştirirken herhangi bir tebeşir, kalem, metre ya da başka bir birim kullanabilirsiniz.

Şimdi elinize herhangi bir cisim, örneğin bir kalem alın. Bu kalemin boyunu bir birim olarak kabul edin ve kalemi bir doğrunun üzerine yerleştirin. Kalemin sol tarafına 0, sağ tarafına 1 yazdığınızda sayı doğrusuna tam sayıları yerleştirmeye başladınız demektir. Bundan sonrası diğer sayıları benzer şekilde sayı doğrusuna yerleştirmek olacaktır. Burada biriminizin kalem boyu olduğunu unutmayın!

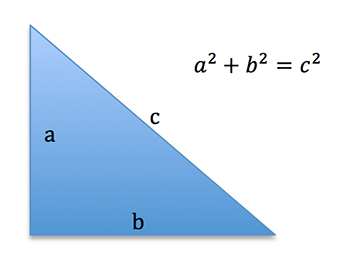
Pisagor, ünlü dik üçgen bağıntısında dik kenarların karelerinin toplamının hipotenüsün (en uzun kenarın) karesine eşit olduğunu söylemiştir. Kendisi ile ilgili anlatılan hikâyeye göre, 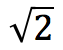 sayısını asla bulamamış olduğu için (o zamanlar irrasyonel sayılar yok tabii) Pisagor bu sayıyı yok saymıştır.  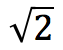irrasyonel bir sayıdır ve devretmeyen ondalık açılıma sahiptir. Yerini bulmak da kolay değildir! Öğrenciler gözlemlediğim kadarıyla sonuçların hep tam sayı olmasını ister. Hatta sonuç rasyonel bir sayı çıktığında sorunun doğru olup olmadığını sorgularlar. Ben buna Pisagor etkisi diyorum. Negatif sayılar, rasyonel ve irrasyonel sayılar tam sayılara göre daha az seviliyor sanki!

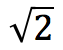, sayı doğrusunda nerede yer alır? Bu soru sorulduğunda gelen ilk cevap 1 ile 2 arasında olduğudur. Doğru! Ancak şunu gözden kaçırmayın: o aralıkta sayı doğrusundaki sayılar kadar nokta vardır. Yani çoktur!

Sorumuz şöyle: 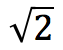sayısının tam olarak nerede olduğunu basitçe nasıl bulabiliriz? Ya da bulabilir miyiz?

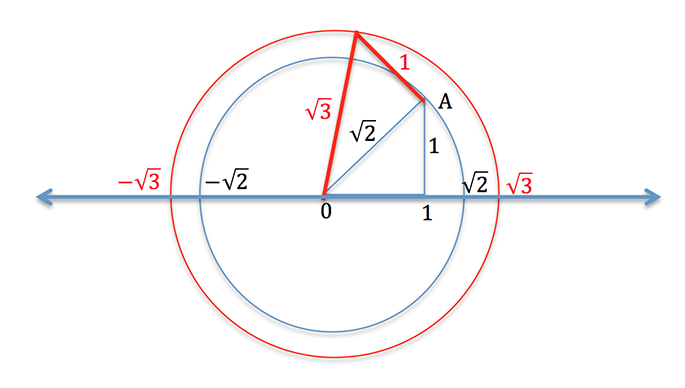
Yukarıdaki şekli elde etmek için, az önce yaptığınız gibi, bir kalemle tam sayıları sayı doğrusuna yerleştirin. Kaleminizi 1 sayısını yerleştirdiğiniz noktaya dik olarak koyup 0 ile 1’i birleştirdiğinizde bir dik üçgen elde edersiniz. Bu üçgende hipotenüsün uzunluğu 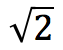olacaktır. Şimdi pergelinizle merkezi 0 olan ve yarıçapı hipotenüs uzunluğunda olan bir çember çizin. Çemberin doğruyu kestiği noktalar  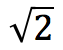ve 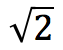 - olacaktır! A noktasından 1 birim daha dik çıkıp yeni bir dik üçgen çizerseniz bu kez karşınıza  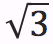çıkacaktır. Artık gerisi size kalmış.

Not: Başlıktaki 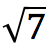 sayısını denemeyi unutmayın! İyi eğlenceler.