Pizzayı Eş Dilimlere Ayırmanın Yeni ve Farklı Yolları
Liverpool Üniversitesinden matematikçiler, bir pizzayı merkezden geçen doğrular ile kesmek yerine daha farklı bir geometrik tasarım geliştirdiler.

grafvision/ iStock.com
Liverpool Üniversitesinden matematikçiler, bir pizzayı merkezden geçen doğrular ile kesmek yerine daha farklı bir geometrik tasarım geliştirdiler. Bu yeni dilimleme yöntemini geliştirme fikri, matematikçilerin uzun zamandır ilgisini çeken şu soru ile ortaya çıktı: “Daire şeklindeki bir pizzanın en az bir dilimi merkeze değmeyecek şekilde eşit büyüklükte dilimlere ayrılabilir mi?”
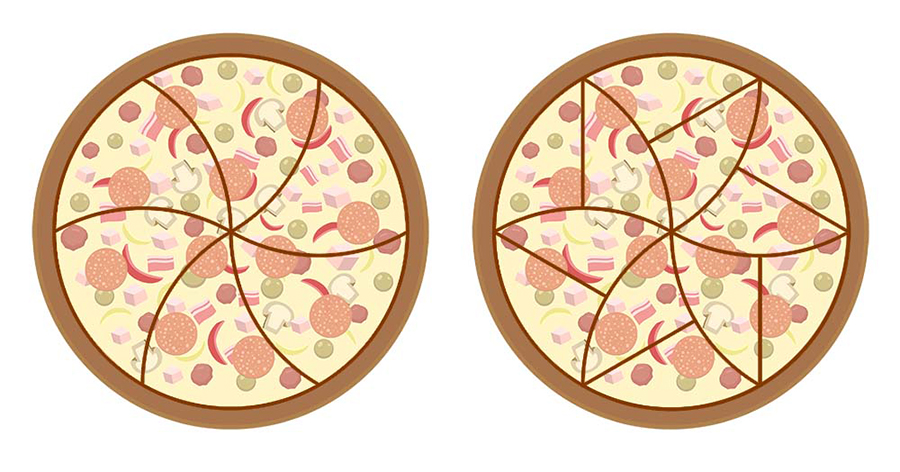
Daha önce bir pizzayı en az bir dilimi merkeze değmeyecek şekilde 12 eş parçaya ayırmanın mümkün olduğu gösterilmişti. Bunun için araştırmacılar pizzayı merkezinden geçen ve bir önceki doğru ile 30 derecelik açı yapan doğrularla kesmek yerine, pizzayı merkezden geçen kavisli üç eğri ile 6 eş parçaya ayırdılar. Ardından bu parçaları da ikiye bölerek şekildeki gibi eş dilimler elde ettiler.
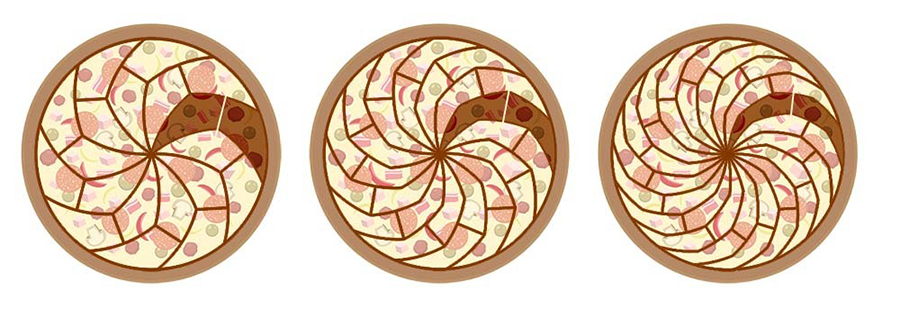
Liverpool Üniversitesinden Dr. Joel Haddley ile doktora öğrencisi Stephen Worsley ise bu kavisli eğrilerin kullanıldığı dilimleme yöntemini herhangi bir tek sayıda kenara sahip dilimler elde etmek için geliştirdiler. Daha sonra tek sayıda kenarı olan bu dilimleri de ikiye bölerek eş parçalar elde ettiler. Örneğin aşağıdaki pizza görsellerinde sadece merkezden geçen kıvrımlı eğriler ile kesilen, farklı renkle işaretlenmiş pizza dilimleri sırasıyla 5, 7 ve 9 kenarlı. Her bir dilimin ikiye bölünmesiyle birbirine eş parçalar elde ediliyor.
Bir düzlemin aralarında boşluk olmadan geometrik şekiller ile kaplanmasına matematikte tesselasyon ya da mozaikleme denir. Dikdörtgen taşların belirli bir kurala göre dizilmesiyle oluşan kaldırımlar bir tesselasyon örneğidir. Bir düzlemin tek tip geometrik şekil ile hiç boşluk kalmayacak şekilde kaplanması ise "monohedral tesselasyon’’ olarak isimlendirilir. Burada mono kelimesi "bir", hedral kelimesi de "şekil" anlamına gelir. Bu durumda, birbirine eşit pizza dilimleri ile oluşturulan desenler ise birer monohedral tesselasyon örneğidir.

mikroman6/Moment/Getty Images
Çalışma ile ilgili ayrıntılı bilgiye buradan ulaşabilirsiniz.
Kaynaklar:
- https://news.liverpool.ac.uk/2016/01/12/mathematicians-reveal-new-way-to-slice-pizza-equally/
- https://arxiv.org/pdf/1512.03794v1.pdf
- https://www.newscientist.com/article/dn28743-mathematicians-invent-new-way-to-slice-pizza-into-exotic-shapes/

















