Meşhur Matematik Problemi: ‘‘Taşınan Kanepe Problemi’’ Çözüldü
Bir koridordaki 90 derecelik bir köşeyi sıkışmadan geçebilecek kanepenin alanının maksimum değerini bulmayı amaçlayan “taşınan kanepe problemi”, altmış yıla yakın bir süredir çözülemeyen bir matematik problemiydi.
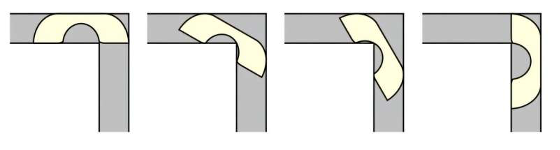
Koridor perspektifinde hareket eden bir kanepe
Taşınan kanepe problemi, evini taşıyan hemen herkesin karşılaştığı bir soruna dayanan, çözümünü bekleyen ünlü bir matematik problemiydi. Sorun, genişliği 1 birim olan bir koridordaki 90 derecelik bir köşeden sıkışmadan geçebilecek kanepenin maksimum alanını belirlemekti. İlk bakışta basit görünen bu problem, matematikçi Leo Moser tarafından 1966 yılında ortaya atıldığından bu yana çözülememişti. Ancak Güney Kore’deki Yonsei Üniversitesi’nde doktora sonrası araştırmacı olan matematikçi Jineon Baek, yakın zamanda bu sorunu çözmeyi başardı.
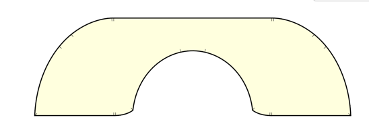
Problemdeki kanepe
Baek, çözümü yani köşeden sıkışmadan geçebilecek kanepenin maksimum alanını “Gerver kanepesi” olarak bilinen, görseldeki kanepe şeklini kullanarak hesapladı. Ön kısmı kavisli olan bu kanepe formu 1992 yılında Joseph Gerver tarafından önerilmişti. Gerver, taşınan kanepe probleminin çözümü için bu formun maksimum alana sahip olabileceğini önermiş ancak bunu matematiksel olarak kanıtlayamamıştı.
Baek, Gerver’in önerdiği kanepe formunu temel alarak genişliği 1 birim olan bir koridordaki 90 derecelik bir köşeden sıkışmadan geçebilecek kanepenin maksimum alanını 2,2195 birim kare olarak hesaplayarak problemi çözüme ulaştırdı. Baek’in problemin çözümüne yer verdiği makalesine buradan ulaşabilirsiniz.
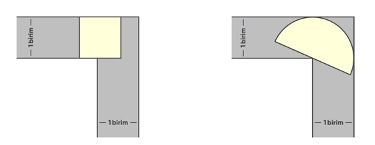
Taşınan kanepe probleminin çözümü, ilk olarak kare ve yarım daire gibi diğer geometrik şekiller kullanılarak denenmişti. Örneğin kare şeklindeki bir kanepenin 1 birim genişlikte ve 90 derecelik köşesi olan bir koridordan geçebilmesi için kanepe alanının maksimum 1 birim kare, yarım daire şeklinde bir kanepe alanının ise maksimum π/2 birim kare olması gerektiği hesaplanmıştı.
Çizer: Serap Keskin Kıdış
Koridorda hareket eden kare ve yarım daire şeklindeki kanepeler
Problemi çözmek isteyen araştırmacılar daha karmaşık şekillerde kanepeler de tasarladılar. Örneğin 1968 yılında matematikçi John Michael Hammersley’in tasarladığı ve kendi ismini verdiği kanepenin alanı π/2 + 2/π olarak yani yaklaşık 2,2074 olarak hesaplanmıştı. Ancak bu değer, taşınan kanepe problemi için Baek tarafından hesaplanan maksimum alandan daha küçüktür.
Kaynaklar: