Astronomide Uzaklıklar Paralaks Yöntemiyle Nasıl Hesaplanır?

Bir nesneye olan bakış doğrultunuz değiştiğinde o nesnenin arka planda yer alan daha uzaktaki nesnelere göre konumunun değişmesine paralaks denir. Paralaks gezegen, yıldız, gök ada gibi uzaydaki gök cisimlerinin Dünya’dan uzaklıklarını belirlemek için kullanılan matematiksel bir yöntemdir. Peki paralaks yönetimiyle uzaklıklar nasıl hesaplanır? Bu yöntem ile hangi uzaklığa kadar ölçüm yapılabilir?

Bilim Genç sesli yayınlarını SoundCloud, YouTube, Spotify, Google ve Apple podcast kanallarımız üzerinden dinleyebilir ve güncel içeriklerimizden anında haberdar olmak için kanallarımızı takip edebilirsiniz.

 

Bu sesli yayını

---

Seslendirme Metni:

Astronomide Uzaklıklar Paralaks Yöntemiyle Nasıl Hesaplanır?

Uzaya ve bilime meraklı dostlar merhaba! Bilim Genç sesli yayınının bu bölümünde astronomide cisimlerin uzaklıklarının nasıl hesaplandığından bahsedeceğim. Durmaksızın gelişen bilim ve teknoloji sayesinde Dünya üzerinde herhangi iki nokta arasındaki uzaklığı belirlemek günümüzde artık çok kolay. Ancak Güneş sisteminin dışındaki veya daha ötedeki nesnelerin uzaklığını belirlemek için başka yöntemler kullanmamız gerekiyor. Uzaklık belirleme yöntemlerinin sayısı ve sesli yayının süresini dikkate alarak bu bölümde, sadece paralaks (ıraklık açısı) yönteminden bahsedeceğim. Aynı zamanda konuyla ilgili bazı temel kavramlardan da bahsetmeyi planlıyorum. Diğer uzaklık belirleme yöntemlerini ise bir sonraki bölümde sizlere anlatacağım.

Radar Tekniği Nedir? Radar Tekniği Nasıl Kullanılır?

Uzayda mesafeler arttıkça uzaklık hesabı yapmak giderek zorlaşır. Örneğin Güneş sistemindeki karasal gezegenlere, asteroitlere veya kuyruklu yıldızlara bir radar sinyali göndererek sinyalin size gelmesini bekleyebilirsiniz. Radar sinyali ışık hızında ilerler. Işığın boşluktaki hızı saniyede 300.000 km olduğuna göre, bu değerin radar sinyalinin gidiş-geliş süresinin yarısı ile çarpımı o nesnenin sizden uzaklığını verecektir. Mesela Ay’ın uzaklığı bu yolla güncel olarak hesaplanmaktadır. Radar sinyali sayesinde sadece cismin uzaklığı değil aynı zamanda cismin şekli hakkında da bilgiye sahip olabilirsiniz. Ancak çok daha uzakta yer alan nesneler için radar tekniği işe yaramaz.

Elbette Güneş sisteminin dışına veya gök adamızın derinliklerine uzay araçları göndererek sürekli olarak size sinyal göndermesini ve bu sayede uzaklığı duyarlı şekilde hesaplamayı düşünebilirsiniz. Ancak gök adamız o kadar büyük bir yer ki bir uzay aracının Güneş’e en yakın yıldız Proxima Centauri’ye ulaşması bile binlerce yıl sürer. Bu da insan hayatına kıyasla çok uzun bir süredir. Gök adamızda ortalama 400 milyar başka yıldız olduğunu hatırlatmak istiyorum. Uzayın derinliklerine gönderilen uzay araçlarına örnek olarak Voyager verilebilir. 1977 yılında uzaya gönderilen Voyager uzay araçlarından Voyager 1 şu an 24 milyar km uzaklıkta ve yoluna devam ediyor. Bu mesafe çok büyük gibi görünebilir ancak Proxima Centauri yıldızına olan uzaklığın yaklaşık 1.700’de 1’ine eşittir. Voyager uzay aracının 46 yılda gidebildiği mesafe bu. O hâlde radar kullanmadan veya bir uzay aracı göndermeden uzaklığı hesaplamanın başka yolları olmalı.

Paralaks (Iraklık Açısı) Nedir? Paralaks Yöntemi Nedir? Paralaks Etkisi Nedir?

Güneş sisteminin ötesindeki yıldızların uzaklığını belirlemek için kullanılan ilk yöntem paralaks yöntemidir.  Bugüne kadar paralaks kelimesini kullanmamış olabilirsiniz. Ancak farkında olmadan hepimiz aslında bu geometrik olayı deneyimleriz. Paralaks kısaca şöyle tanımlanabilir: Bir nesneye olan bakış doğrultunuz değiştiğinde o nesnenin arka planda yer alan daha uzaktaki nesnelere göre konumu da değişir. İki basit örnekle paralaks etkisinin ne demek olduğunu daha net bir şekilde açıklayalım.

Paralaks Etkisine Hangi Örnekler Verilebilir?

Hareket hâlindeki bir arabada olduğunuzu ve arabanın camından dışarıya baktığınızı hayal edin. Yol kenarındaki bariyerleri görmek istediğinizde net bir görüntü elde edemezsiniz. Çünkü aracınız belli bir hızda ilerlediği için bariyerlerin görüntüsü de görüş alanınızda hızlı hareket edecektir. Ancak daha uzaktaki nesnelere, örneğin uzaktaki bir ağaca veya binaya bakmak istediğinizde, o nesnelerin görüş alanınızdaki hareketi daha yavaş olacağı için onları daha net görebilirsiniz. Yani siz hareket hâlindeyken, size yakın olan nesneler uzaktaki nesnelere kıyasla daha hızlı bir şekilde görüş alanınızdan çıkar, hareketinizin aksi yönünde görüş alanınızdan kayıp gider. Bu kayma miktarı size yakın olan nesneler için daha büyük olacaktır. Örneğin hareket hâlindeyken yakındaki nesnelerin net bir fotoğrafını çekebilmek işte bu nedenle zordur.

Paralaksın ne olduğunu daha iyi kavrayabilmek için vereceğim ikinci basit örneği ise şu an bu ses kaydını dinlerken bulunduğunuz yerde uygulayabilirsiniz. Kollarınızdan birini uzatın ve işaret parmağınız ile duvardaki veya dilediğiniz bir yerdeki herhangi bir nesneyi hedef alın. Bunu yaparken gözlerinizden biri kapalı ve açık olan diğer gözünüzle işaret parmağınızla hedef aldığınız o nesneye adeta nişan alıyorsunuz. Kolunuzu ve parmağınızı hiçbir şekilde oynatmadan açık olan gözünüzü kapatıp diğer gözünüzü açarak işaret parmağınızın hedef aldığı noktaya tekrar bakıyorsunuz. Parmağınızın, ilk durumda hedef aldığınız nesneyi göstermediğini, bir miktar yan tarafa kayarak uzaktaki başka bir noktayı işaret ettiğini göreceksiniz. Hedef aldığınız doğrultu bir kayma göstermiştir. İşte buna paralaks denir.

Aslında kolunuz, parmağınız ve başlangıçta hedef aldığınız nesnenin yeri değişmedi. Değişen şey bakış açınızdı. Gözlenen nesnenin konumundaki bu açısal yer değiştirme olayı, yani paralaks etkisi, astronomide uzaklık belirlemek için kullanılan bir yöntemdir. Ancak en yakını trilyonlarca kilometre ötede olan yıldızların göreli olarak yer değiştirmesini ölçebilmek için iki gözün arasındaki mesafeden daha büyük bir mesafeye ihtiyaç vardır. Nitekim, iki bakış doğrultusu arasındaki mesafe ne kadar büyükse paralaks etkisi o kadar fazla olacaktır. Ancak Dünya’nın iki ucuna yerleştirilmiş teleskoplarla bir yıldıza bakmak bile yıldızın göreli yer değiştirmesini belirlemek için yeterli olmaz. Çünkü Dünya’nın çapı, yıldızın uzaklığına kıyasla çok küçüktür. O hâlde birbirinden çok daha uzakta bulunan iki noktadan gözlem yapmamız gerekir.

Bir yıldızın bizden uzaklığını paralaks yöntemiyle belirlemek için, Dünya üzerinde iki uzak noktaya gitmek yerine, Dünya’nın Güneş etrafındaki hareketinden yararlanırız. Peki bu ölçümü tam olarak nasıl yapıyoruz?

Uzayda Paralaks Yöntemi Nasıl Kullanılır? Paralaks Etkisi Nasıl Hesaplanır?

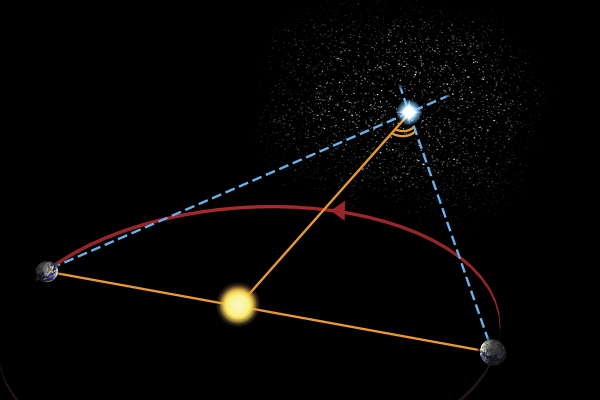
Yılın belli bir zamanında, mesela mart ayında, bir yıldızı gözlediğinizi ve o yıldızın gökyüzündeki konumunu işaretlediğinizi varsayalım. Altı ay sonra, yani eylül ayında, o yıldızı tekrar gözlediniz ve gökyüzündeki konumunu tekrar işaretlediniz. Altı ay arayla yaptığınız gözlemlerle aynı yıldız için işaretlediğiniz iki konumun, arka planda çok daha uzakta yer alan yıldızların konumuna göre gökyüzünde farklı yerlerde olduğunu göreceksiniz. Yıldız gökyüzünde açısal olarak bir miktar yer değiştirmiş gibi görünecektir. Aslında değişen şey yıldızın gökyüzündeki gerçek yeri değil bakış açınızdır.

Paralaks Açısı Nedir?

Dikkat ederseniz Dünya’nın Güneş etrafındaki yörüngesinde, yıldızı gözlemek için altı ay arayla kullandığımız her iki konum için bir dik üçgen oluşur. Köşelerinde Dünya, Güneş ve yıldızın olduğu bir dik üçgen. Her bir dik üçgenin tabanı Dünya-Güneş arası mesafeyi temsil eder ve dik üçgenin tepesindeki açının tam karşısında bulunur. İşte bu açıya “paralaks açısı” denir. Yıldız ne kadar uzakta ise paralaks açısı o kadar küçük, yıldız ne kadar yakın ise paralaks açısı o kadar büyük olacaktır.

Trigonometrik Paralaks Nedir?

Üçgeni belirledikten sonra yapılacak tek şey, antik çağlardan beri bilinen trigonometrinin basit bir işlemini uygulamak olacak. Bir açının tanjantı o açının karşısındaki kenar ile açıya komşu dik kenarın bölümüne eşittir. Açıyı biliyorsunuz. O açının karşısındaki kenar ise Dünya-Güneş arası mesafe yani 150 milyon kilometredir. Bulmak istediğimiz şey ise açıya komşu dik kenarın uzunluğu yani yıldızın Güneş’e olan uzaklığıdır. İşte bu nedenle bu yönteme tam adıyla “trigonometrik paralaks” denir.

Peki neden altı aylık bir zaman aralığında gözlem yaptık? Çünkü Dünya altı ay içinde yörüngesinde 180 derece ilerlemiş yani başlangıç konumuna kıyasla yörüngesinin yarısını tamamlamış ve Güneş’in diğer tarafına geçmiş olur. Böylece, az önce belirttiğim gibi bir dik üçgen elde edip uzaklık hesabını basitçe yapabiliriz. Evet! Tahmin ettiğiniz gibi Dünya’nın Güneş etrafındaki yörüngesini çember kabul ettim. Aslında Dünya’nın yörüngesinin şekli tam olarak bir çember değildir ancak çembere çok yakındır. O nedenle bu kabul işlemlerde çok büyük bir sorun yaratmaz.

Parsek Nedir?

“Paralaks açısı 1 yay saniyesi olan bir ışık kaynağının uzaklığı 1 parsektir.” denir. Parsek bir başka uzunluk birimidir ve 1 parsek 3,26 ışık yılına denk gelir. Bir ışık yılı yaklaşık 9,5 trilyon km olduğuna göre 1 parsek yaklaşık 30 trilyon kilometredir. Yay saniyesi, yay dakikası ve derece kavramları ise açıyı temsil eder. Örneğin etrafınızda bir tam tur döndüğünüzde 360 derecelik bir açıyı taramış olursunuz. Her derecenin 60’ta 1’i 1 yay dakikasına ve her yay dakikasının 60’ta 1’i ise 1 yay saniyesine eşittir. 1 saatin 60 dakika ve 1 dakikanın 60 saniye olması gibi. Kolunuzu uzatın ve serçe parmağınızı kaldırın. Serçe parmağınızın gökyüzünde kapladığı açısal alan yaklaşık 1 derecedir. İşte onun 3.600’de 1’i bir yay saniyesi demektir. Sanırım 1 yay saniyesinin gökyüzünde ne kadar küçük bir açısal alan kapladığını anlamış olduk.

Paralaks Yöntemi ile Hangi Uzaklığa Kadar Ölçüm Yapılabilir?

Peki paralaks yöntemi ile hangi uzaklığa kadar ölçüm yapılabilir? Uzaydaki teleskoplar ile yapılan gözlemlerle paralaks açısı 0,001 yay saniyesi olan yıldızların uzaklığı hesaplanabilir. Bu da 1.000 parsek yani yaklaşık 30 katrilyon km ötedeki cisimlerin uzaklığını hesaplayabilmek anlamına gelir. Avrupa Uzay Ajansına ait, dokuz yıldır çalışan GAIA isimli uzay teleskobu ise 100 kat daha duyarlı gözlemler yapabilmekte ve gök adamız içindeki milyarlarca yıldızın uzaklık ve konum bilgisini hesaplayabilmektedir. Gök adamızın görsel dalga boyundaki çapı 30.000 parsek yani yaklaşık 100.000 ışık yılıdır. Kısaca söylemek gerekirse, gök adamızın dışındaki ışık kaynaklarının uzaklığını belirleyebilmek için paralaks dışında başka yöntemler kullanmak zorundayız. Bu yöntemleri bir sonraki sesli yayınımızda anlatacağım.

Bu sesli yayını sonlandırmadan önce önemli bir ayrıntıdan da bahsetmem gerekiyor. Paralaks açısına neden olan ve bakış açımıza bağlı bu göreli hareket dışında yıldızların kendine ait öz hareketleri de vardır. Yıldızlar bir yıldız kümesinin veya yıldız grubunun üyesi olduğu için hem o küme içerisinde hem de gök ada merkezi etrafında hareket ederler. Ancak yıldızlar bize çok uzak olduğu için öz hareketleri nedeniyle gökyüzündeki yer değiştirmeleri bir insan hayatı süresince fark edilemez. İşte bu nedenle uzun yıllar boyunca yıldızlar sabit zannedilmiştir. Ancak unutmayın! Evrende sabit hiçbir şey yoktur. Hatta evrenin kendisi bile sürekli genişler.

Bilim Genç sesli yayınının bir bölümünün daha sonuna geldik. Bu bölümde astronomide uzaklık hesaplamak için kullanılan yöntemlere bir giriş yapmış olduk. Galaksimizdeki yıldızlara ve diğer ışık kaynaklarına olan uzaklığı belirlememizi sağlayan paralaks yöntemini günlük yaşamdan örneklerle açıkladım ve ayrıca bazı temel bilgileri de sizlerle paylaştım.

Bilim Genç sesli yayınlarının bir sonraki bölümünde, etrafımızı saran evreni keşfetmeye devam edeceğiz. Şimdilik hoşça kalın!

Kaynaklar:

• Topal, S., Kaostan Kozmosa Evrenin Hikayesi, Destek Yayınları, 2020
• https://astronomy.swin.edu.au/cosmos/t/trigonometric+parallax
• https://sci.esa.int/web/gaia/home

Hazırlayan ve Seslendiren Hakkında:

Doç. Dr. Selçuk Topal

Van Yüzüncü Yıl Üniversitesi Fizik Bölümü

Yüksek Enerji ve Plazma Fiziği Anabilim Dalı