Bir Yüzeyi Desen Tekrar Etmeyecek Şekilde Kaplamaya İmkân Veren Şekil: “Şapka”
Sokakta yürürken kaldırım taşlarının şekillerine ya da nasıl döşendiklerine pek dikkat etmeyiz. Bu yazıda kimi zaman üzerine basıp geçtiğimiz zeminlerdeki döşemelerin ya da kafamızı çevirip bakmadığımız duvarlardaki fayansların oluşturduğu desenlerden yola çıkarak matematikçilerin üzerinde çalıştığı ve yakın zamanda heyecan verici yeni bir gelişme yaşanan bir konudan bahsedeceğiz.

Afonkin_Yuriy / Stock
Gün içerisinde gittiğimiz farklı mekânlarda değişik örneklerine rastladığımız döşeme ve süslemelerden oluşan desenler ayrıca sanat eserlerinde, kumaşlarda, kâğıtlarda veya elektronik ortamda çeşitli süslemelerde de karşımıza çıkıyor. Günlük hayatta rastladığımız örneklerde genelde kare, eşkenar üçgen, altıgen gibi basit şekiller kullanılsa da daha iddialı tasarımlarda farklı şekillerin daha önce benzeri olmayan biçimde bir araya getirildiğini görebiliyoruz. Örneğin Selçuklu ve Osmanlı mimarisinde rastladığımız süslemeler bu tasarımların en ilgi çekici örneklerinden.

Huseyin BAS / iStock
Selçuklu mimarisindeki tekrar eden desenlerden oluşan süslemeler
Yakın zamanlarda matematikçiler, tek bir şekil kullanarak bir deseni tekrarlamadan düzlemi kaplayabilen 13 kenarlı bir şekil keşfetti. Matematikçiler uzun zamandır böyle bir şekil arıyordu. Ancak ortaya matematikçiler için şaşırtıcı derecede basit bir şekil çıktı. Bu buluşun malzeme biliminden dekorasyona çeşitli alanlarda uygulamaları olabileceği düşünülüyor.
Ayrıntılara girmeden ve “Neymiş bu şekil?” sorusuna cevap vermeden önce kullandığımız terimleri açıklayalım. Çünkü matematikte tanımlar çok önemlidir.
Bu döşeme veya süslemeler yerde, duvarda veya herhangi bir düz zeminde bulunabilir. Önemli olan düz bir yüzey kullanılması ve yüzeyin tamamen kaplanmasıdır. Yani arada boşluk kalmaması gerekir. Ayrıca kaplama için kullandığımız şekiller birbirinin üzerine gelmemelidir.
Matematikçiler sonsuzu sever. Bu nedenle sınırlı bir yüzeyin kaplanmasıyla değil, bir düzlemin geometrik şekillerle kaplanması problemi ile ilgilenirler. Bu geometrik şekillere gerçek hayattaki kullanımlarından yola çıkarak “karo” diyoruz.
Kaplamalarda tek bir şekilden oluşan karolar kullanabileceğimiz gibi farklı şekillerden oluşan karo kümeleri de kullanılabiliriz.
|
|
|
|
GeoGebra'da altıgen şeklinde karo ile yapılan kaplama |
GeoGebra'da altıgen ve eşkenar dörtgen karolar ile yapılan kaplama |
Günlük hayatta karşılaştığımız kaplamaları incelediğimizde, çoğunda kaplamanın bir kısmının kendini tekrar ettiğini görebiliriz. Bu tür kaplamalara “periyodik kaplamalar” diyoruz. Peki hangi şekillerle periyodik kaplama yapılabilir? Bu amaçla eşkenar üçgen, kare ve dikdörtgen kullanabiliriz. Aslında periyodik kaplamalarda tekrar eden kısımlar paralelkenarlar ile gösterilebilir. Aşağıdaki kaplama örneklerinde paralelkenarları istediğiniz gibi şekillere ayırabilirsiniz. Sonuçta elde edilen kaplama periyodik olacaktır.
|
|
|
Düzgün çokgenler göz önüne alındığında, yalnızca arıların favori şekli olan altıgen karo kullandığımız zaman periyodik kaplamalar yapılabiliyor. Sadece düzgün beşgen kullanarak herhangi bir kaplama yapılamadığını da belirtelim. Bunun nedeni, beşgenin bir iç açısının 108 derece olması. Üç tane beşgeni ortak bir noktada birleştirmeye çalıştığımız zaman arada 36 derecelik bir boşluk kalıyor.
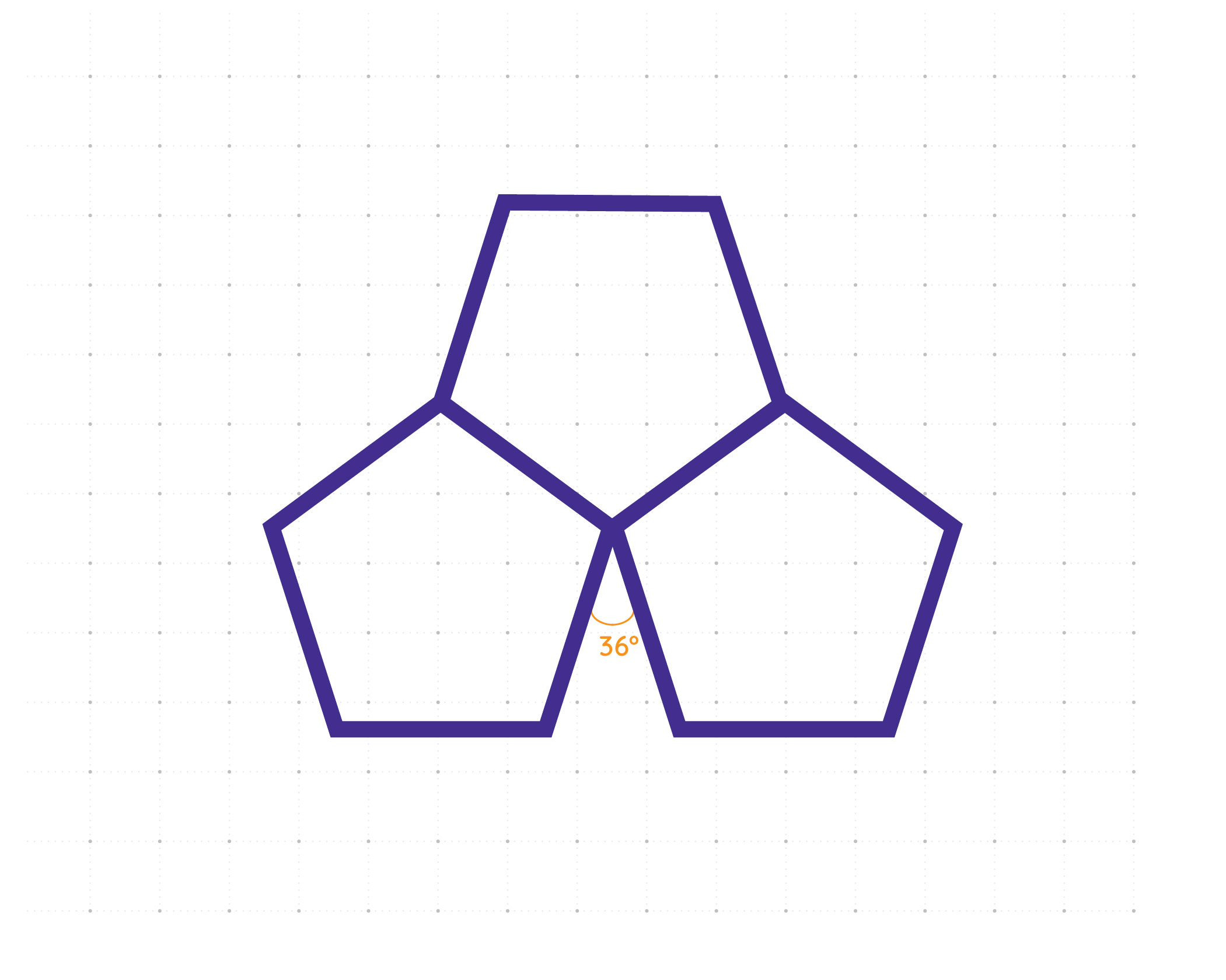
Benzer şekilde 7 ve daha fazla kenara sahip düzgün çokgenlerde de çokgenin bir iç açısı 120 dereceden fazla olduğu için, üç tanesini ortak bir köşede birleştirmek mümkün değil. İki tanesini birleştirmeye çalıştığımızda da yine arada boşluk kalıyor. Ancak bunları farklı şekildeki karolar ile beraber kullanarak bir düzlemi kaplamak mümkün.

RonFullHD / iStock
Sekizgen ve eşkenar dörtgen karolar kullanılarak yapılan bir periyodik kaplama
Periyodik kaplamalar kadar periyodik olmayan kaplamalarla da son derece ilginç desenler ortaya çıkarılabiliyor. Bu tür kaplamalar ayrıca fizikçiler ve kimyacıların kristalimsi olarak isimlendirilen malzemelerin doğasını ve davranışını anlamalarına yardımcı oluyor.

Eric Heller / Science Photo Library
Kristalimsi malzemeler, atomların sıralandığı ancak yinelenen bir modele sahip olmadığı bir yapıya sahiptir.
Bazı şekiller farklı biçimde bir araya getirilerek hem periyodik hem periyodik olmayan kaplamalar yapılabilir. Matematikçiler sadece periyodik olmayan kaplamalar yapmak için nasıl şekiller kullanılması gerektiği üzerine uzun zamandır çalışıyorlardı.
1961'de matematikçi Hao Wang, periyodik olmayan kaplama yapılabilecek her karo kümesinin düzlemi periyodik olarak da kaplayabileceğini iddia etmişti. Ancak kendi öğrencisi Robert Berger, sadece periyodik olmayan kaplama yapılabilen 20.426 şekilden oluşan bir karo kümesi bularak bu iddiayı çürüttü. Sonra periyodik olmayan kaplama yapılabilecek karo sayısını 104’e indirdi.
1974’te Nobel ödüllü fizikçi Roger Penrose biri altılı, diğer ikisi ikili olan üç tane farklı karo kümesi buldu. Penrose bu karoları beşgen şeklinin dönel simetri özelliğini kullanarak oluşturdu. Bu yüzden bu karolara “pentapleks karolar” adı verildi.

Whiteway / iStock
Pentapleks karo
O zamandan beri, matematikçiler periyodik olmayan kaplama yapılabilecek karo sayısını bire indirmeye çalışıyorlardı. Amaç sadece tek bir şekilde karo kullanarak düzlemi periyodik olmayacak biçimde kaplamaktı. Bu karoya einstein ismi takıldı. Bu isim, bildiğimiz ünlü fizikçinin adından değil, ifadenin Almanca “tek taş” anlamana gelmesinden kaynaklanıyor.
Aranan bu einstein İngiltere’nin Yorkshire bölgesinde yaşayan ve emekli bir matbaa teknisyeni olan David Smith tarafından keşfedildi. Smith, beraber çalıştığı bilgisayar bilimcisi ve matematikçi üç araştırmacı ile “şapka” ismini taktıkları şekli nasıl keşfettiklerini ve bunun olası kullanımlarını anlatan bir makale yazdı.
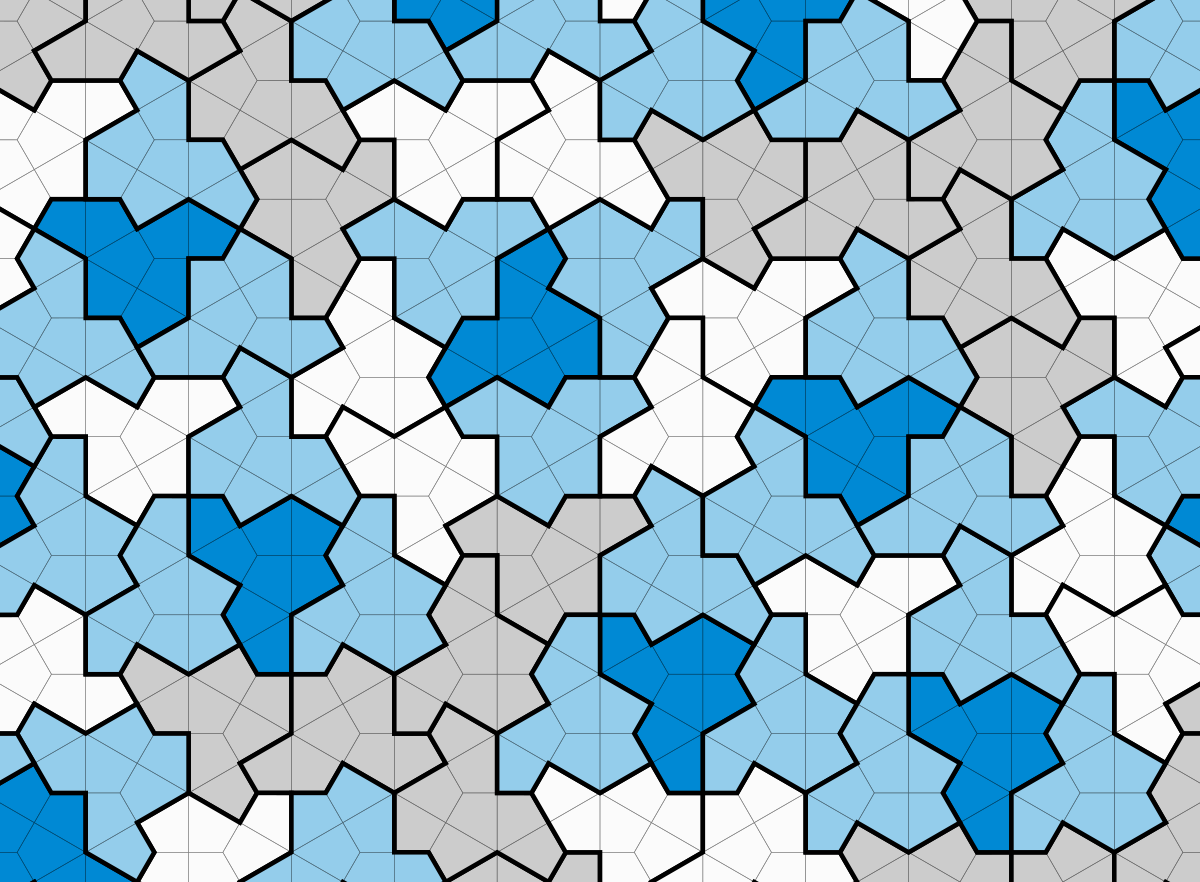
University of Waterloo CC BY 4.0
“Şapka” adı verilen karolardan oluşan bir yüzey kaplaması
Aşağıdaki bağlantı adresinde şeklin adım adım nasıl oluşturulduğunu görebilirsiniz.
https://www.geogebra.org/m/wtv5zeyx
Kaynaklar:
- Arık, M., Sancak, M., Pentapleks Kaplamalar, TÜBİTAK Popüler Bilim Kitapları, Ankara, 2007.
- Smith, D. ve ark., “An aperiodic monotile”, arXiv, 2023.
- https://phys.org/news/2023-03-geometric-tiled.html
- https://www.livescience.com/newly-discovered-einstein-tile-is-a-13-sided-shape-that-solves-a-decades-old-math-problem
- https://en.wikipedia.org/wiki/Aperiodic_tiling
Yazar Hakkında:
Dr. Öğr. Üyesi Yeşim İmamoğlu
Boğaziçi Üniversitesi Matematik ve Fen Bilimleri Eğitimi Bölümü





















