GeoGebra ile Çemberde Thales Teoremi

Etrafımıza baktığımızda kaç tane çember görüyoruz? Halıdaki desenler, çanak antenler, yediğimiz simitler, telefon tuşları… Çember, farkında olmadan günlük yaşamımızda çok fazla kullandığımız kavramlardan bir tanesi. Peki, çember nedir? Çember, “düzlemde sabit bir noktaya eşit uzaklıkta bulunan noktaların oluşturduğu kapalı geometrik şekil” olarak tanımlanır.

Bir çember oluşturmak için doğrusal olmayan üç nokta yeterlidir. Şimdi, GeoGebra programını kullanarak bir çember çizelim ve çemberde Thales teoremini inceleyelim. Bunun için önce rastgele iki nokta seçmemiz gerekiyor (Şekil 1).

Şekil 1

Rastgele iki nokta seçtikten sonra, çemberi oluşturmak için gerekli olan üçüncü noktayı nasıl ve nerede seçmeliyiz? Sabit bir nokta seçip bu noktaya eşit uzaklıktaki tüm noktaları bulmak yerine bu iki noktaya doğrusal olmayan üçüncü noktayı belirleyerek çemberi kolaylıkla çizebiliriz (Şekil 2).

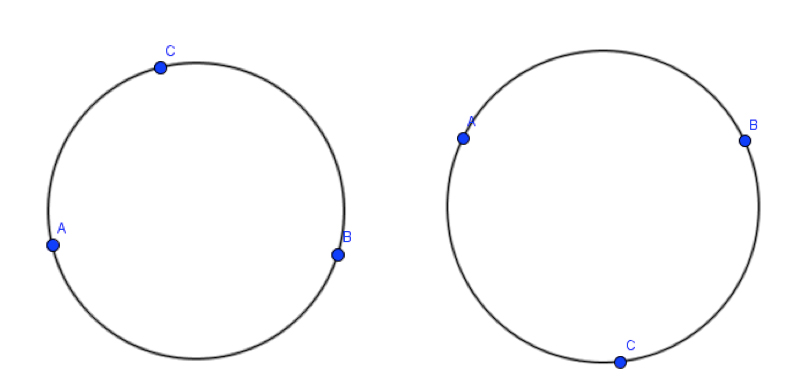
Şekil 2

Şekil 2’de görüldüğü gibi seçilen üçüncü nokta diğer iki noktayla doğrusal değil ise “üç noktadan geçen çember” araç çubuğuyla bir çember çizebiliriz. Bunun yanı sıra çember tanımından yararlanarak yani sabit bir noktaya eşit uzaklıkta bulunan noktaları bir sürgü yardımıyla belirleyerek de çember çizmemiz mümkün (Şekil 3).

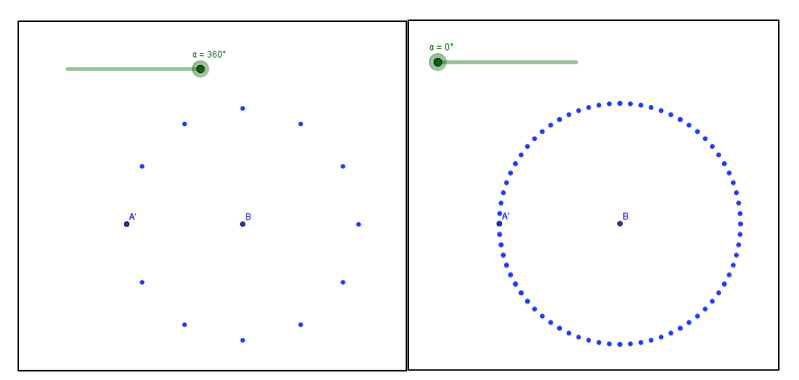
Şekil 3

Çemberde merkez açı ve çevre açı kavramlarını duymuşuzdur. Köşesi çemberin merkezinde olan açıya merkez açı denir. Bir merkez açının ölçüsü gördüğü yayın ölçüsüne eşittir. Köşesi çemberin üzerinde, kenarları bu çemberin kirişleri olan açıya çevre açı denir. Şekil 4’te görüldüğü gibi AOB açıları merkez açı, ACB açıları ise çevre açıdır. 

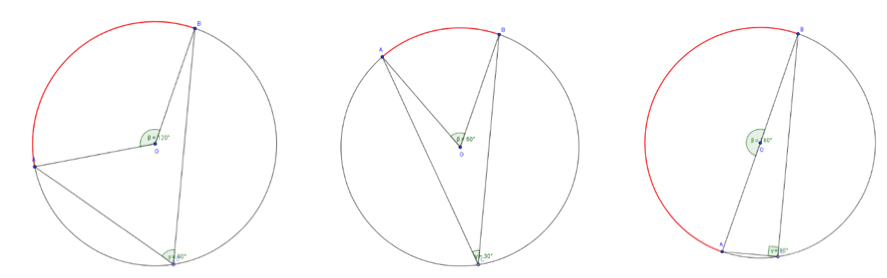
Şekil 4

Merkez açı ile çevre açı arasında bir bağıntı bulabilir miyiz? Şekil 4’teki örneklerde görüldüğü gibi merkez açının ölçüsü çevre açınınkinin 2 katıdır. Şimdi, çemberde açılarla ilgili bir uygulama yapalım. Ancak önce çember ve özellikleri üzerine çalışmalar yapan, dönemin ünlü matematikçilerinden Thales’ten bahsedelim.

Matematik insanlar için her zaman merak konusu olmuştur. Eğer işin içinde merak varsa felsefe de vardır. Thales felsefeyle ilgilenmiş ve felsefenin getirdiği analitik düşünce sistemini matematik üzerinde kullanmış bir bilim insanıdır. Tam adı Miletli Thales’tir ve MÖ 624 yılında doğmuş, MÖ 546 yılında ölmüştür. Bir Anadolu filozofu olan Thales, Sokrates öncesi dönemde yaşamıştır. Felsefenin ve bilimin öncüsü olarak kabul edilen Thales aynı zamanda ilk filozoflardan biridir. Mısır’daki matematik okulunun da ilk öğrencisidir. Antik Yunan’da yaşayan yedi büyük bilginden en eskisi ve en ünlüsüdür. Hayatı hakkında kesin ve ayrıntılı bilgiler dönemin şartlarından dolayı günümüze ulaşamamıştır.

Bir daire içine üçgen çizilmesi problemini çözümleyen Thales’in ters açıların eşitliğini doğruladığı söylenir. Üçgenlerin özellikleri ve Thales bağıntıları, Mısır’daki piramitlerin yüksekliğinin bulunmasında kullanılmıştır. Şimdi, Thales teoremi olarak bilinen “köşesi çember üzerinde olan ve çapı gören çevre açının dik açı olduğu” teoremi dinamik geometri yazılımımız olan GeoGebra’da gösterelim.

Öncelikle çemberin çapını oluşturmak için düzlemde herhangi iki nokta seçip “iki noktadan geçen yarım çember” komutunu kullanarak bir yarım çember oluşturalım (Şekil 5).

Şekil 5

Çemberde çapı gören açının dik açı olduğunu göstermek için öncelikle çember içinde bu açıyı oluşturalım. Bunun için çember üzerinde rastgele dinamik bir nokta seçelim (C noktası). Şekil 6’da görüldüğü gibi, bu noktayı çap üzerinde bulunan A ve B noktaları ile birleştirerek ABC üçgenini oluşturalım (Şekil 6).

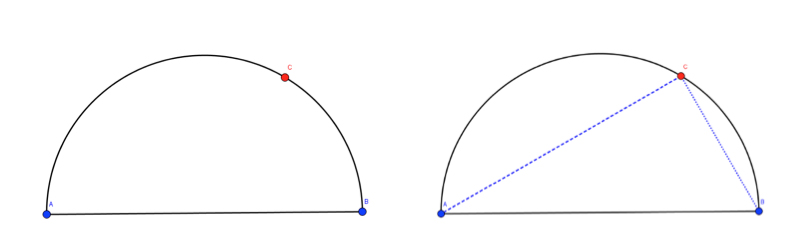
Şekil 6

Şekilde 7’de görüldüğü gibi, oluşturduğumuz üçgende iç açıların ölçülerini belirlemek için  araç çubuklarından “açı” komutunu kullanabiliriz (Şekil 7).

Şekil 7

 

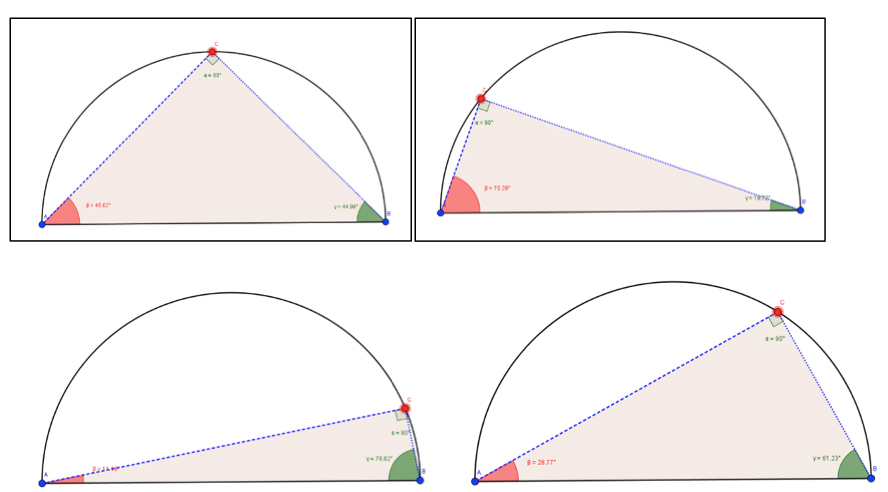
Şekil 8

 

Üçgenin iç açılarının ölçülerini bulduktan sonra çember üzerinde seçtiğimiz C noktasını hareket ettirdiğimizde, çapı gören açının her zaman 90 derece yani dik açı olduğunu gözlemleyebiliriz (Şekil 8). Verilen etkinliğe https://www.geogebra.org/m/z7Mvg6WK adresinden ulaşabilirsiniz. Benzer teoremlerin GeoGebra yardımıyla ispatını ve doğrulanmasını siz sevgili okuyucularımıza bırakıyoruz.