Matematik, Fizikçiler İçin Neden Önemli?

"Matematik ne işimize yarar?”

Bu cümleyi belki daha önce duymuş ya da doğrudan kendimiz kurmuş olabiliriz. Özellikle ne işe yarayacağının farkında olmadığımız zor matematik sorularıyla boğuşurken! Matematik, günlük hayattaki sayma ve hesaplama gibi basit işlerimizi kolaylaştırdığı gibi evreni kavrama konusunda da bize yol gösterir. Bu yazıda ise matematiğin gücünden ve fizik ile arasındaki sıkı ilişkiden bahsedeceğiz.

Fizikçiler de tüm bilim insanları gibi evrenin işleyişini matematik ile anlamaya çalışır. Çünkü matematik bir anlamda evrenin dilidir. Fiziksel kuramlar da bu dille ifade edilir. 

Fiziksel kuramlar sadece gözlediğimiz olayları açıklamakla kalmaz, aynı zamanda henüz gözlemediğimiz ya da gözleyemediğimiz durumlar hakkında da tahminler yapar. Tüm bunlar matematik sayesinde mümkün olur.

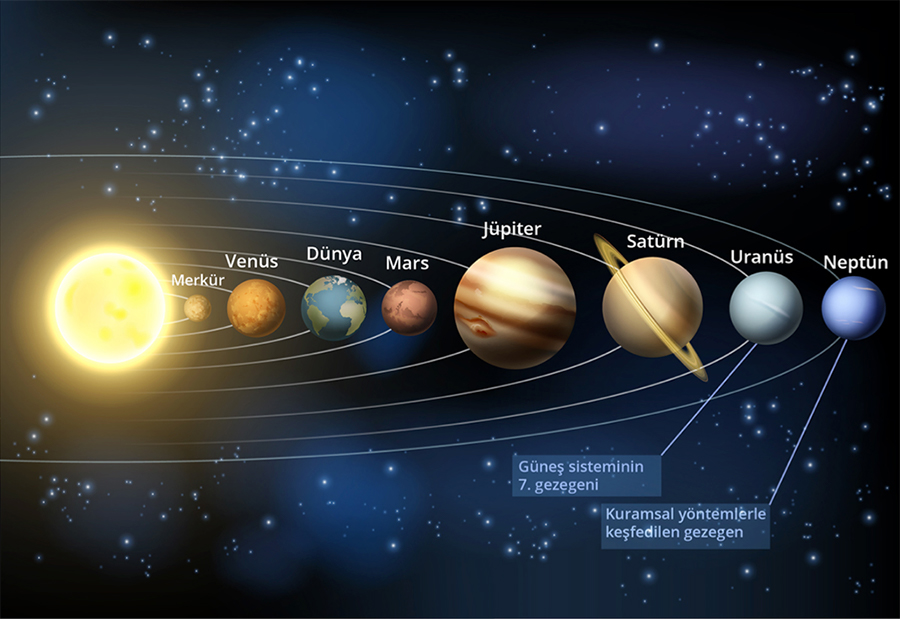
Matematiğin gücünü anlamamıza yardımcı olan en çarpıcı örneklerden biri Neptün’ün keşfidir. Neptün, diğer gezegenlerin aksine teleskopla değil, kuramsal yöntemlerle ve hesaplamalarla keşfedilmiş bir gezegendir. Bu örnekte olduğu gibi matematik, henüz gözlenmemiş olsa da Güneş sisteminde var olması gereken gezegenlere dair ipuçları verir. 

Nasıl mı?

Dönemin bilim insanları 1781 yılında keşfedilen, Güneş sistemindeki 7. gezegen olan Uranüs’ün hareketinde gözlenen anormalliği, Uranüs’e en yakın gezegenler olan Satürn ve Jüpiter’in varlığı ile açıklamanın mümkün olmadığını fark etmişlerdi. Uranüs’ün gözlenen hareketinin Newton’un kütle çekim kanunu ile açıklanabilmesi için yakınında bir başka gezegenin daha bulunması gerektiğini 1845 yılında Fransız Urbain Le Verrier ve İngiliz John Couch Adams birbirlerinden bağımsız olarak gösterdiler. Neptün’ün varlığı, 1846 yılında gözlemlerle de doğrulandı. Fiziksel kuramları ifade etmek için kullandığımız güçlü dil, yani matematik, olmadan Uranüs’ün yörüngesini gözlemleyerek Neptün’ün varlığını tahmin edemezdik. 

 

 

Matematiğin gücüne tek örnek Neptün’ün keşfi ile sınırlı değil elbette. İngiliz fizikçi Paul Dirac’ın antimaddenin varlığını tahmin etmesi de matematik sayesinde mümkün oldu.

Madde atomlardan, atomlar da negatif yüklü elektron, pozitif yüklü proton ve yüksüz nötronlardan oluşur. Kütleleri sıradan parçacıklar ile aynı fakat yükleri zıt işaretli olan elektron (pozitron) ve proton (antiproton) da bir araya gelerek bir antiatom, bu antiatomlar da bir araya gelerek antimaddeyi oluşturabilir. Madde ve antimadde karşılaştığında birbirlerini yok eder ve bu yok oluş sonucunda toplam kütlelerinin eş değeri kadar enerji açığa çıkar.

Peki, matematik antimaddenin varlığının tahmin edilmesini nasıl sağlayabildi?

1900’lü yılların başında evren algımızı temelden değiştiren iki önemli kuram geliştirilmişti. Bunlardan biri, ışık hızına yakın hızlarda hareket eden cisimlerin davranışını açıklayan Einstein’ın özel görelilik kuramı, diğeri ise atomaltı parçacıkların davranışını başarılı bir biçimde öngören kuantum kuramıydı. Birbirinden bağımsız geliştirilen bu iki kuramı birleştirmeye çalışanlardan biri de Pauli Dirac’dı ve kendisini bir sürpriz bekliyordu.

 

İngiliz fizikçi Paul Dirac

Dirac’ın bu iki kuramı içerecek şekilde formül hâline getirdiği denklemde, beklenildiği gibi elektronun varlığına işaret eden çözümlerin yanı sıra hiç beklenmedik bir çözüm daha vardı. Bu çözüm, aynı elektron gibi ancak yükü ters olan bir başka parçacığın varlığına işaret ediyordu. Bu kafa karıştırıcı ve öngörülmeyen çözüme karşı gelen bir parçacık evrende henüz hiç gözlenmemişti! Kuramda bir yanlışlık mı vardı? Eğer yoksa bu çözüm göz ardı edilebilir miydi? Ya da kuramsal hesaplar, böyle bir parçacığın varlığına dair bir ipucu vererek evreni anlamaya yönelik insanlığın zihninde yeni bir ufuk mu açıyordu?

Dirac’ın kuramı çok geçmeden doğrulandı. Antimaddenin varlığını öngören kuram yayımladıktan 3 yıl sonra yani 1931 yılında Carl D. Anderson, yükü pozitif olan elektronu (pozitronu) deneysel olarak ilk kez gözlemledi. Sadece elektronun değil diğer temel parçacıkların da antiparçacıklarının olduğu kısa sürede anlaşıldı ve bu parçacıklar da daha sonraları deneysel olarak gözlemlendi. Matematiğin açtığı bu kapıyla antimaddeden oluşabilecek bir evrenin var olma ihtimali, bilim kurgunun ötesinde bilim dünyasında konuşulmaya başlandı.

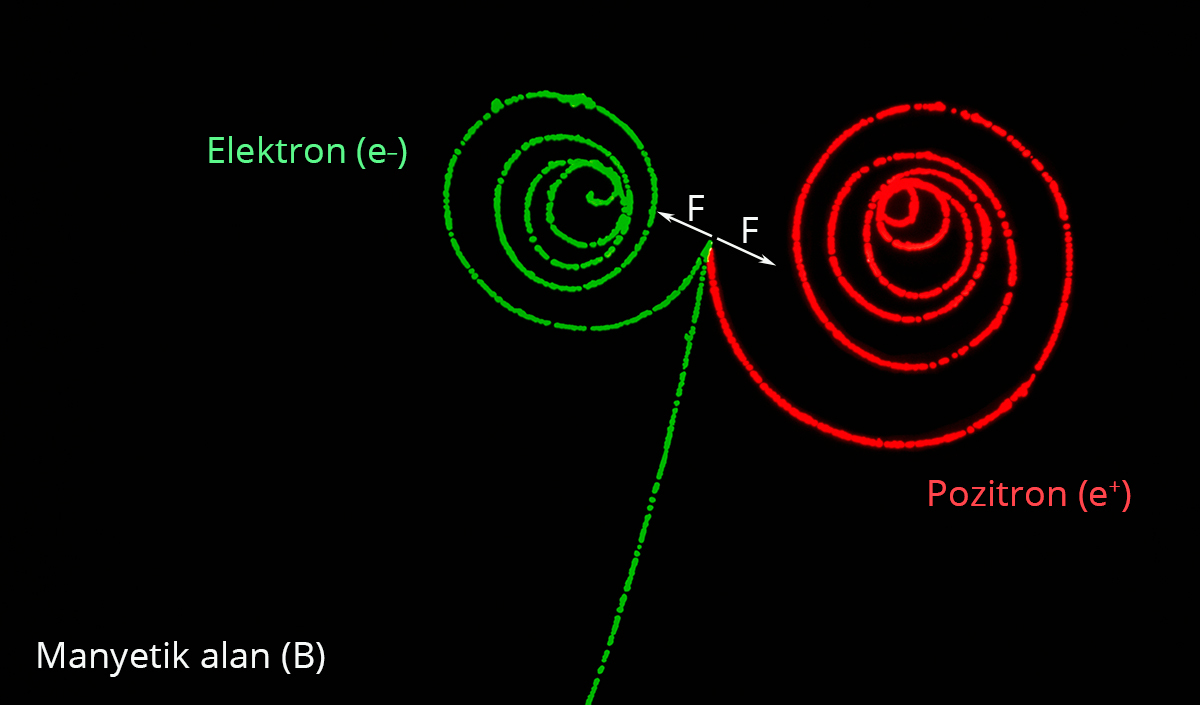
Bir manyetik alana (B) giren elektron ve pozitrona kütleleri aynı,yükleri zıt işaretli olduğundan aynı büyüklükte fakat ters yönde bir kuvvet (F) etki eder.

Antimaddenin keşfine yol açan örnekte olduğu gibi bilimin tarihsel serüvenine bakıldığında fizik ve matematiğin hep birbirini geliştiren iki alan olduğu görülebilir. Bazen fizik matematiğin gelişimine yol açarken bazen de matematik fiziğin önünde gitmiştir. Başka bir ifadeyle bazen gözlenen bir doğa olayını anlamak için yeni matematiksel yöntemler geliştirilirken bazen de bir uygulamasının olup olmayacağı önceden bilinmeden geliştirilen bir matematik kuramı sonradan fiziksel bir olayı açıklamak için kullanılmıştır. Bu ikinci duruma Riemann geometrisi iyi bir örnektir. 19. yüzyılın ortalarında Bernhard Riemann’ın geliştirdiği geometri o dönemde bir uygulama alanı bulamazken, 20. yüzyılın başında Einstein’ın genel görelilik kuramını geliştirmek için aradığı geometri tam olarak Riemann geometrisiydi.

Parmak saymakla başlayan matematiğin serüveni, evreni kavramaya yönelik keşiflerle üst düzeye erişti. Matematikte yeni ilerlemeler kaydedildikçe bilim ve teknolojideki gelişmeler daha baş döndürücü seviyeye ulaşacak. 

Kaynaklar:

• https://www.universetoday.com/120681/mathematics-the-beautiful-language-of-the-universe/amp/ 
• https://plus.maths.org/content/unreasonable-relationship-between-mathematics-and-physics 
• https://earthsky.org/human-world/today-in-science-discovery-of-neptune/ 
• https://historyofinformation.com/detail.php?id=4004 
• https://bilimgenc.tubitak.gov.tr/makale/antimadde-nedir