Etkileşimli Matematik: GeoGebra ile Açılar

Başta gelişmiş ülkelerde olmak üzere etkileşimli öğretime verilen önem hızla artıyor. Gelişen ve değişen dünyada teknolojinin önemi her alanda vurgulanırken matematiği anlamak ve matematik öğretimini kolaylaştırmak için de teknolojinin avantajlarından faydalanılıyor. Son yıllarda bilgisayarların yanı sıra etkileşimli matematik yazılımları, akıllı tahtalar, tabletler, grafik hesap makineleri gibi teknolojik araçlar matematik öğrenimi ve öğretiminde etkili bir şekilde kullanılmaya başlandı. Bunlardan dinamik matematik yazılımları olarak adlandırılan araçlar, özellikle geometri ve cebirdeki birçok konunun öğretilmesinde yaygın olarak tercih ediliyor. Bu yazılımlardan The Geometer’s Sketchpad, Cabri, Cabri 3D ve Cindirella’yı kullanmak için ücret ödemek gerekirken, GeoGebra dinamik yazılımı dünyanın her yerinde ücretsiz olarak indirilebiliyor. 

İsmini geometri (geometry) ve cebir (algebra) kelimelerinin birleşiminden alan GeoGebra, 2001 yılında Avusturyalı Markus Hohenwarter tarafından geliştirildi. Hohenwarter bu yazılım sayesinde birçok ödüle layık görüldü. 2006 yılından itibaren Avusturya Eğitim Bakanlığı okullardaki ve üniversitelerdeki matematik eğitimini geliştirmek ve güçlendirmek amacıyla bu yazılımın ücretsiz olarak kullanılmasını destekledi. 2007 yılında Uluslararası GeoGebra Enstitüsü’nün kurulmasıyla, yazılım tüm dünyada eğitimciler ve öğrenciler tarafından yaygın bir şekilde kullanılmaya başlandı.

GeoGebra, cebir ve geometride karşımıza çıkan birçok denklem ve şeklin aslında statik (durağan) olmadığını, bu denklem ve şekillerin sonsuz sayıda türevlerinin olabileceğini dinamik bir şekilde görmemize katkıda bulunuyor. Örneğin açılar konusu geometrinin en temel konularından biridir ve ileri seviye geometri konularının öğrenilmesi için hayli önemlidir. Ülkemizdeki geometri öğretiminde açı, “başlangıç noktaları aynı olan iki ışının birleşimi” şeklinde tanımlanıyor, ancak uluslararası öğretim programlarında açının üç farklı tanımından bahsediliyor ve öğrencilerin açı kavramını öğrenmesi için bu tanımların eş zamanlı verilmesi gerektiği savunuluyor: iki doğru arasındaki dönme miktarının ölçüsü (dönme tanımı), başlangıç noktası aynı olan iki ışının kesişimi (köşe tanımı), iki yarı düzlemin kesişimi ile meydana gelen bölge (iki doğrunun kesişimi ile oluşan iç bölge tanımı). Bazı kaynaklarda ise açının fiziksel özellikleri kullanılarak tanımlandığına değiniliyor. Bu tanımlara bakıldığında, aslında açı kavramının iki ışının kesişiminden oluşan statik bir şekilden öte daha kapsamlı bir kavram olduğu görülüyor.

Üçgen, çokgen, üç boyutlu cisimler, trigonometri ve birçok ileri geometri ve cebir konularının öğrenilmesi için GeoGebra yazılımının kullanılmasının faydalı olabileceği düşünülüyor. Örneğin bu yazılım, açı kavramı öğrenilirken farklı açıları görmek ve keşfetmek amacıyla kullanılabilir (https://tube.geogebra.org/m/LwF3laPg).

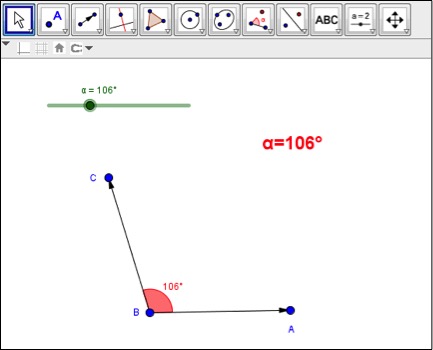
Verilen linkte bir açı, bir sürgü ve açının ölçüsü görülüyor. Sürgü olarak adlandırılan doğru parçası GeoGebra yazılımının faydalı araçlarından biridir. Bu örnekte, sürgüyü sürükleyerek 0-360 derece arasındaki tüm açıları görebilirsiniz. Bu sayede açı dediğimiz zaman zihnimizde tek bir nesneden öte, dinamik, birden fazla şekil haline dönüşebilen bir kavram oluşacaktır. GeoGebra yazılımını nasıl indirebileceğinizi, kullanabileceğinizi ve bu etkinliği nasıl tasarlayabileceğinizi aşağıdaki videodan öğrenebilirsiniz.

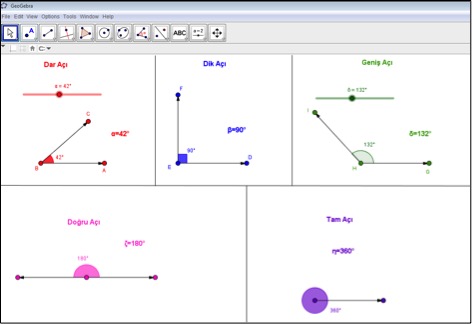
Açı tanımı ile ilgili kavram yanılgılarından bir tanesi de açı çeşitlerinden kaynaklanıyor. Yaptığımız bir araştırmada 5. sınıf öğrencisine açı nedir diye sorduk ve “dik açı 90 derecedir, dar açı 90 dereceden küçüktür, geniş açı 90 dereceden büyüktür” cevabını aldık. Bu öğrencinin açı çeşitleri ile açı kavramını zihninde birleştirdiği ve dik açıyı diğer açı çeşitlerini tamamlamak için referans aldığı söylenebilir. Öğrencileri açı tanımında olduğu gibi açı çeşitleri konusunda da ezbere dayalı bir öğretimden uzaklaştırmak amacıyla GeoGebra’dan faydalanılabilir. Bunun için dar açı, dik açı, geniş açı, doğru açı ve tam açı kavramları sürgüler yardımı ile tanıtılabilir (https://tube.geogebra.org/material/simple/id/jOm7AbD5). Bu sayede, “90 dereceden küçük açılar dar açıdır” ezber tanımından uzaklaşılıp bu açılar interaktif ortamda gözlemlenerek neden 90 dereceden küçük açılara dar açı denildiği daha iyi kavranabilir.

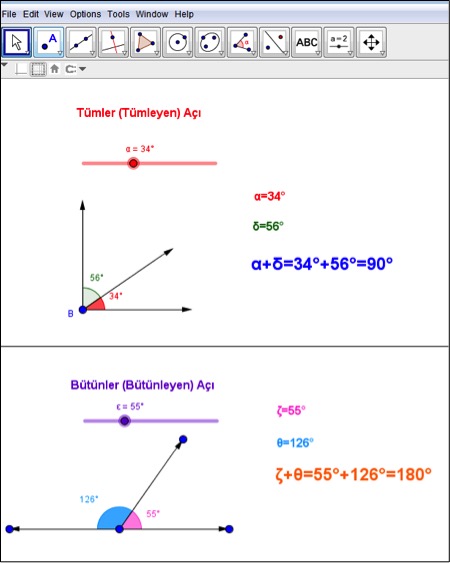
Açılar ile ilgili kavram yanılgısına sebep olan bir diğer terim ise tümler (tümleyen) ve bütünler (bütünleyen) açılardır. Tümler açı “toplamları 90 derece olan iki açı”, bütünler açı ise “toplamları 180 derece olan iki açı” şeklinde tanımlanır. Peki, bu açıların toplamlarının 90 derece ve 180 derece olması ne demektir? Komşu iki açı (yani bir kenarları ortak olan iki açı) ele alınarak tümler ve bütünler açılar keşfedilebilir. Örneğin sürgü yardımıyla bir dar açının ölçüsü değiştirilerek bu açının tümler açısındaki değişim görülebilir (https://www.geogebra.org/m/Vif82hO9). Böylece açı ölçüleri değişmesine rağmen açıların toplamının değişmediği, her zaman 90 derece olduğu etkileşimli bir şekilde kavranmış olur. Aynı şekilde sürgü yardımıyla bütünler iki açının toplam ölçüsünün her zaman 180 derece olduğu gözlemlenebilir.

Geometrinin en temel kavramlarından biri olan açı ve açı ile ilgili en temel özellikler, gelişmiş ve gelişmekte olan ülkelerin geometri öğretim sistemlerinde olduğu gibi, ülkemizde de GeoGebra yardımıyla etkileşimli biçimde öğrenilebilir ve öğretilebilir. İlk etkinlik için verilen bilgiler doğrultusunda GeoGebra ile ikinci ve üçüncü etkinliklerin tasarlanmasını siz sevgili okuyucularımıza bırakıyoruz.

Kaynaklar:

• Keiser, J. M., “Struggles with developing the concept of angle: Comparing sixth grade students’ discourse to the history of the angle concept”, Mathematical Thinking and Learning, Cilt 6, Sayı 3, s. 285-306, 2004.
• Mitchelmore, M. ve White, P, “Development of angle concepts by progressive abstraction and generalisation”, Educational Studies in Mathematics, Cilt 41, Sayı 3, s. 209-238, 2000.
• Yigit, M., “Pre-service Secondary Mathematics Teachers’ Conceptions on Angles”, The Mathematics Enthusiast, Cilt 11, Sayı 3, s. 707-736, 2014.