Fraktal Desenler Oluşturalım
Deneyler köşesinin bu projesinde gittikçe küçülen, küçüldükçe karmaşıklaşan yapıları yani fraktalları inceliyoruz.

Ted Kinsman / Science Photo Library
Bilmekte Fayda Var!
Matematikçi Benoit Mandelbrot’un dediği gibi, “Ne bulutlar küre şeklindedir ne de dağlar koni. Ağaç kabukları pürüzsüz değildir ve şimşek düz bir çizgide yol almaz.”. Doğa sadelikten uzak, girintili-çıkıntılı, parçalı yüzeyler barındırır. Peki sonlu ögeler içeren geometri dışında bu yüzeyleri nasıl tanımlayabiliriz? Cevap fraktallarda gizli.
Fraktal Nedir?
Fraktallar, aynı desenlerin farklı boyutlarda tekrar etmesiyle oluşan geometrik şekillerdir. Fraktal terimi Mandelbrot tarafından “düzensiz veya parçalı” anlamına gelen Latince fractus kelimesinden türetilmiştir.
Fraktalların Özellikleri Nelerdir?
En temelde fraktallar; basit bir şekilde başlayan, giderek daha karmaşık hâle gelen ve sürekli yinelenen bir modelin ya da formülün görsel bir ifadesidir. Kusursuz bir matematiksel fraktalda her desen kendisinin daha küçük kopyalarından oluşur ve bu küçük kopyalar sonsuza kadar devam eder.
Fraktal Örnekleri Nelerdir?
Romanesco karnabaharı ya da diğer adıyla piramit karnabahar, spiral şeklindeki yeşil konileriyle dikkat çeker. Karnabahar, bu konilerin farklı boyutlarda birbirini tekrar etmesiyle şekillenir. Karnabaharın bir parçasına yakından bakıldığında tüm karnabahardaki desenin aynısı görülür. Bu nedenle Romanesco karnabaharı, sadece bir bitki değil aynı zamanda çarpıcı bir fraktal görünüme sahip bir matematik harikasıdır.

maraqu / iStock
Kadrajımızı bu kez en küçüklerin dünyasına çevirelim. Besi yerinde yetiştirilip büyüme süreçleri incelenen bakteri kolonilerinin, ortam koşulları elverişsiz hâle geldikçe, daha karmaşık bir yapıya bürünerek fraktallar oluşturduğu görülüyor.

Besi ortamında büyüyen bakteri kolonisinin oluşturduğu fraktal deseni
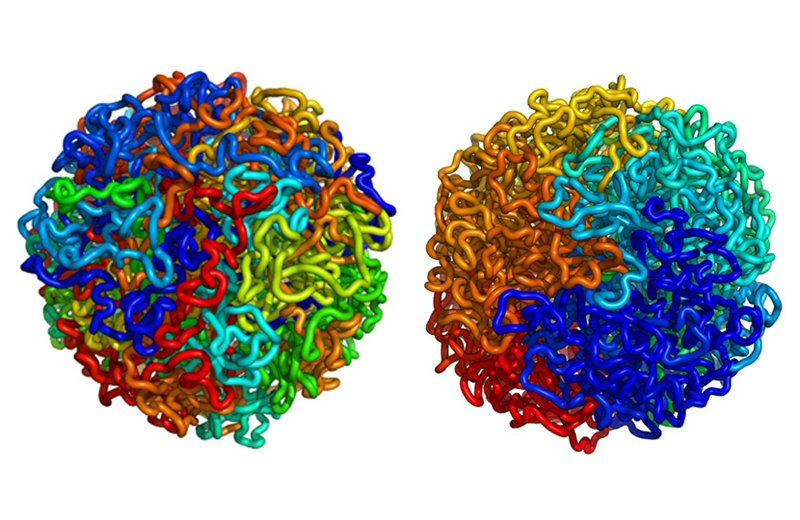
Fraktallar vücudumuzda da var! Örneğin damarlarımız hatta DNA’larımız bile fraktallardan oluşuyor. Massachusetts Teknoloji Enstitüsündeki fizikçilerle birlikte çalışan genetikçiler, DNA’nın "fraktal globül" olarak adlandırılan bir katlanma şekli oluşturduğunu buldular. Bu mimari yapı, hücrenin DNA'yı sıkı bir şekilde paketlemesini sağlarken düğüm ve karışıklıklardan kaçınmasına yardımcı oluyor. Ayrıca DNA, hücre bölünmesi sırasında kolayca açılıp yeniden katlanabiliyor.
Deneyler köşesinin bu projesinde kendi fraktal desenlerimizi oluşturarak yapılarını inceliyoruz.
Nelere İhtiyacımız Var?
- Akrilik boya
- 2 adet düzgün yüzeyli şeffaf plastik malzeme (Cam da kullanılabilir.)
Ne Yapıyoruz?
Ne Oldu?
Boyayı yüzeyler arasında sıkıştırdığımızda, boyanın viskozitesi (akışkanların akmaya karşı gösterdiği direnç) havaya göre daha fazla olduğu için boya havayı iterek tüm yönlerde eşit olarak dağılır ve disk benzeri bir şekil oluşturur. Yüzeyleri birbirinden ayırdığımızda hava, boyanın içine doğru ilerler ve dengesiz bir sınır yüzeyi oluşturur. Küçük hava girintileri giderek büyür ve hava damarlarına dönüşür. Böylece karmaşık dallanmalar oluşur. Birbirinden ayrılan yüzeyleri yan yana getirdiğimizde ise simetrik bir görüntü oluştuğunu görebiliriz.
Oluşturduğumuz desenler; bulutlara, kıyı şeritlerine, mercan resiflerine ve akciğerlerimizdeki bronşların dallanmasına benzetilebilir. Fraktal desenler çözümlenerek tıp, ekoloji, bilgisayar bilimleri, meteoroloji gibi pek çok alanda yenilikçi uygulamalar geliştiriliyor. Örneğin yapılan bir araştırmaya göre normal vücut hücrelerimizin dış yüzeyi belirli bir fraktal desene sahip değilken, farklılaşarak kanserli bir yapıya dönüşme evresinde olan hücrelerin dış yüzeyinin fraktal bir desene sahip olduğu ortaya çıktı. Çalışmanın, kanserin önüne geçilmesinde önemli bir adım olabileceği düşünülüyor.

Sierpinski üçgeni
Matematiksel bir fraktalın nasıl oluşturulduğunu anlamak için Sierpinski üçgeni ve Cantor setini inceleyebilirsiniz. Dilerseniz doğada yeni fraktal arayışına girebilirsiniz!
Kaynaklar:
- Mandelbrot, B. B., The Fractal Geometry of Nature, San Francisco: W.H. Freeman, 1982.
- Gouyet. J. F., “Physics and fractal structures”, Springer Verlag Gmbh, s. 41-72, 1996.
- https://www.exploratorium.edu/snacks/fractal-patterns
- https://science.howstuffworks.com/math-concepts/fractals.htm
- https://cosmosmagazine.com/science/mathematics/fractals-in-nature/
- https://www.popularmechanics.com/science/environment/a19068718/why-its-impossible-to-accurately-measure-a-coastline/
- https://www.bbc.co.uk/ideas/videos/the-freaky-world-of-never-ending-fractals/p07vddcn?playlist=amazing-animations
- http://www.fractal.org/Bewustzijns-Besturings-Model/Application-Fractal-Geometry.pdf
Yazar Hakkında:

















