Matematiğin Büyüleyen Problemi
Bilim insanları yıllar süren çalışmalar sonucunda x3+y3+z3=k denklemini 1 ile 100 arasında çözümü olduğu bilinen her k pozitif tam sayısı için çözdüler. Diğer taraftan 100’den büyük bazı k sayıları için de çözüme ulaşıldı.
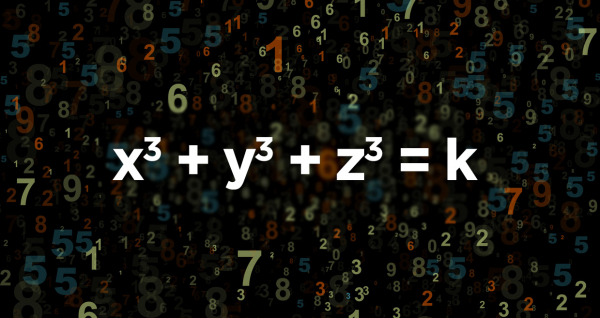
amtitus/iStock.com
Matematikte küplerin toplamı problemi olarak bilinen ve x3+y3+z3=k şeklinde ifade edilen bir polinom denklemi vardır. Bu denklem “Her pozitif k tam sayısı için x,y,z tam sayıları bulunabilir mi?” sorusunun cevabını arar. Peki küplerin toplamı problemi neden bu kadar ilgi çekiyor? Çünkü çoğu tam sayı başka bir tam sayının küpü şeklinde yazılamazken, bu denklemdeki k sayısı üç tam sayının küpler toplamından oluşuyor.
Aşağıdaki örnekleri incelediğimizde, ilk bakışta problemin çözümü çok basitmiş gibi görünebilir:
k=1 için 1=13+03+03 veya 1=13+(-1)3+13
k=3 için 3= 13+13+13 veya 3=43+43+(-5)3.
Fakat tüm pozitif k tam sayıları için problemin çözümü bu örneklerdeki kadar basit değil.
Küpler toplamı probleminin çözümü bilinen k tam sayılarından bazıları şunlar:
k=1, 2, 3, 6, 7, 8, 9, 10, 11, 12, 15, 16, 17, 18, 19, 20, 21, 24, 25, 26, 27, 28, 29, 30, 33, 34, 35, 36, 37, 38, 39, 42, 43, 44, 45...
Yukarıdaki sayılar arasında belirli sayıların eksik olduğunu fark etmişsinizdir. Yapılan çalışmalar 9 ile bölündüğünde 4 veya 5 kalanını veren k sayıları için (örneğin 4, 5 ikilisi; 13, 14 ikilisi; 22, 23 ikilisi) bu problemin çözülemediğini gösteriyor.
Geçmişte 9 ile bölündüğünde 4 veya 5 kalanını vermeyen k=33, k=42 ve k=74 sayıları için de problem çözülememişti. Bu nedenle bu sayıların da çözümü olmadığı düşünülüyordu. Fakat 2016 yılında, Twente Üniversitesinden Dr. Sander G. Huisman problemi k=74 sayısı için çözdü. Ardından 2019 yılında Bristol Üniversitesinden Dr. Andrew Booker problemi k=33 sayısı için aşağıdaki şekilde çözdü:
(8866128975287528)3+(-8778405442862239)3+(-2736111468807040)3=33.
Bu on altı basamaklı sayılara Booker’ın katrilyonlarca farklı olasılık arasından deneme yoluyla ulaştığını sanıyorsanız yanılıyorsunuz. Bu sayılar Booker’ın geliştirdiği bilgisayar algoritması ile bulundu.

monsitj/iStock.com
Daha sonra tüm dikkatler, ilk yüz sayı içinde bulunmasına ve 9 ile bölündüğünde 4 veya 5 kalanını vermemesine rağmen çözülemeyen tek sayı olan k=42 sayısına döndü. Bu sayı ise Massachusetts Teknoloji Enstitüsünde çalışan Dr. Andrew V. Sutherland tarafından aşağıdaki şekilde çözüldü:
(-80538738812075974)3+(80435758145817515)3+(12602123297335631)3=42.
Bu hesaplamaların doğruluğunu kontrol etmek isterseniz hesap makinesi kullanmayın. Büyük ihtimalle hesap makinesi bu kadar büyük sayılarla işlem yapamaz. Bunun yerine çevrimiçi bir programdan faydalanabilirsiniz.
Böylece ilk yüz sayı içinde çözümü olmadığı ispatlanan sayılar hariç tüm sayıların çözümü bulunmuş oldu. Bu durum bilim insanlarını daha zor bir çalışmaya teşvik etti: k=3 sayısı için bilinen çözümlerden farklı bir çözüm daha bulmak. Çünkü yıllar boyunca k=3 sayısı için yeni çözümlerin bulunamayacağına inanılıyordu. k=3 sayısı için yeni çözüm yine Booker ve Sutherland tarafından yakın zamanlarda bulundu. Yukarıda verilen iki farklı çözümün aksine yeni çözüm çok daha zordu:
(569936821221962380720)3+ (-569936821113563493509)3+(-472715493453327032)3=3.
Bu problemin çözümünün olduğu düşünülen ama çözülemeyen en küçük sayısı şu an için k=114. k=3 sayısının daha zor bir çözümünün elde edilmesi, problemin çözülebildiği tüm sayılar için tek bir çözümün bulunmadığını düşündürüyor.
Kaynaklar:
















