Mozaiklerin Matematiği

Yerleri ya da duvarları kaplayan genellikle üçgen, kare, altıgen gibi şekillerden oluşan yüzey kaplamaları hepimiz için hayli tanıdık ve sıradan. Ancak farklı geometrik şekillerden oluşan olağanüstü güzellikteki mozaik tasarımların arkasında karmaşık bir matematiksel yapı var.

Mozaik sanatı farklı geometrik şekillere sahip parçaların aralarında boşluk kalmadan ve parçalar üst üste gelmeden düz bir yüzeyi kaplayacak şekilde birleştirilmesi olarak tanımlanabilir. Bu tür kaplamaların doğadaki örnekleriyle ve insan yapımı uygulamalarıyla sıkça karşılaşırız. Altıgen şekillerden oluşan bal peteği ve kaldırımlar bu kaplamaların çevremizdeki göze çarpan örneklerinden.

Ancak bir yüzeyin farklı parçalar birleştirilerek kaplanması matematikçiler için daha karmaşık anlamlara sahip bir kavram.

Örneğin kaplanmış bir zeminde düz bir şekilde yürüdüğünüzü düşünün. Belli desenlerin düzenli aralıklarla tekrar ettiğini fark ettiyseniz, bu tür kaplamalar periyodik olarak adlandırılabilir. Ancak farklı parçalardan oluşan kaplamaları periyodik olarak tanımlayabilmek için, parçaların iki boyutlu bir düzlemde her iki yönde de düzenli olarak tekrar etmesi gerekir. Bir kaplamanın periyodik olup olmadığını basit bir deneyle anlayabilirsiniz. Bir eskiz kâğıdına çizdiğiniz tekrar eden mozaik deseninin kopyasını, zemin üzerinde döndürmeden belli bir yönde kaydırdığınızda, alttaki desenle eşleşiyorsa mozaiğin periyodik olduğu söylenebilir.

Peki, periyodik olmayan yani belirli düzende tekrar etmeyen bir zemin kaplamasının oluşturulması mümkün müdür?

İlk olarak bir kaplamanın periyodik olmadığına nasıl karar verebiliriz sorusuna cevap vermeye çalışalım. Periyodik olmayan (aperiyodik) mozaiklerin en önemli özelliği mozaiği oluşturan desenlerin belirli aralıklarla tekrar etmemesidir. Bir mozaiğin periyodik olup olmadığını anlamak için kullandığımız yöntemden burada da yararlanabiliriz. Tekrar eden mozaik deseninin kopyasını zemin üzerinde kaydırdığımızda ya da ayna görüntüsünü aldığımızda alttaki desenle eşleşmiyorsa bu tür kaplamalar aperiyodik olarak sınıflandırılabilir. Ancak tekrar eden desen taslağı döndürüldüğünde alttaki desenle eşleşiyorsa yani dönme simetrisine sahipse bu tür kaplamalar aperiyodik olarak sınıflandırılabilir.

İnsanların güzellik anlayışları simetri kavramıyla yakından ilişkili. Simetri, tasarımı oluşturan bileşenlerin daha dengeli yerleşmesine olanak sağlar. Farklı simetri türleri vardır. Yani tekrar eden desen farklı şekillerde hareket ettirilerek, örneğin döndürülerek, öteleyerek ya da ayna görüntüsü alınarak farklı simetri türeleri elde edilebilir.

Peki, sadece aperiyodik bir mozaik tasarımı oluşturabilen parçaların sayısı için bir sınır olabilir mi? Bu soru ilk defa 1961 yılında filozof ve matematikçi Hao Wang tarafından soruldu. Bundan birkaç yıl sonra Robert Berger yaklaşık 20.000 parça kullanarak aperiyodik bir mozaik oluşturmayı başardı ve ilerleyen yıllarda daha az sayıda parça kullanılarak aperiyodik mozaikler yapıldı.

1970’li yılların başında ise İngiliz matematikçi ve fizikçi Roger Penrose altı farklı parçayla periyodik olmayan, ancak dönme simetrisine sahip bir mozaik oluşturmayı başardı.

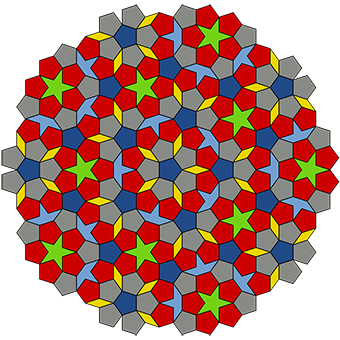
Roger Penrose’un altı farklı parça kullanarak oluşturduğu mozaikte aslında dört farklı şekil var. Ancak mozaikteki farklı renklendirilmiş üç adet beşgen şekil farklı parçalar olarak kabul ediliyor. İlk bakışta desenler tekrar ediyormuş gibi görünse de daha yakından bakıldığında desenlerin tam olarak aynı şekilde tekrar etmediği fark edilebilir.

Roger Penrose daha sonra iki farklı şekle sahip parçalar kullanarak aperiyodik mozaikler oluşturmayı başardı.

Wikipedia

Penrose mozaiğinde uçurtma ve ok adı verilen parçalar (parçalar birleştirildiğinde iç açıları 72°-108° olan bir eşkenar dörtgen elde ediliyor) bir araya getirilerek aperiyodik mozaik desenleri oluşturmak mümkün. Roger Penrose’un diğer bir aperiyodik mozaiğinde iç açıları 72°-108° ve 36°-144° olan eşkenar dörtgen şekilde iki farklı parça kullanılıyor.

Wikipedia

Penrose mozaiğini oluşturan parçalar kullanılarak periyodik olan yani belli aralıklarla düzenli olarak tekrar eden mozaikler de oluşturulabilir.

Bu parçaların aperiyodik bir mozaik oluşturacak şekilde bir araya getirilmesini sağlamak için çeşitli yöntemler uygulanabilir. Bunlardan biri köşelerinde farklı renklerde işaretler bulunan parçaların, aynı renkteki işaretler üst üste gelecek şekilde birleştirilmesi. Diğeri ise parçaların üzerindeki genellikle dairesel desenlerin uyumlu bir şekilde bir araya getirilmesi. Penrose mozaikleri oluşturmak için uygulanabilecek başka kurallar da var. Özellikle üzerinde desenler bulunan parçaların birleştirilmesiyle oluşturulan mozaiklerde ortaya çıkan desenler daha kolay fark edilebiliyor.

İki farklı şekildeki parçalar kullanılarak oluşturulan Penrose mozaiklerinin dikkat çekici diğer bir özelliği ise, mozaiklerin kapladığı alan genişledikçe kullanılan parçaların sayılarının oranının, altın oran olarak bilinen 1,618 sayısına yaklaşması.

Harvard Üniversitesi Fizik Bölümü’nde çalışan araştırmacı Peter J. Lu, Penrose mozaiği olarak bilinen desenlerin izlerine 15. yüzyıl İslam mimarisinde rastladı. Sonuçları Science dergisinde yayımlanan çalışmada araştırmacılar mozaiklerin uçurtma ve ok olarak bilinen şekillerin birleşiminden oluşan daha büyük parçaların bir araya getirilmesiyle yapıldığını, böylece geniş yüzeyleri kaplayan mozaiklerin hatasız bir şekilde birleştirilebildiğini düşünüyor.

Aperiyodik mozaiklerdeki düzen atom ölçeğinde de karşımıza çıkıyor. Bilim insanları quasikristal olarak bilinen yapılarda atomların bulunduğu konumların oluşturduğu desenlerin hiçbir zaman tekrar etmediğini, ancak mükemmel bir düzende olduğunu belirledi. Normal kristallerde ise atomların konumlanma şekli simetriktir ve belli bir düzende tekrar eder yani periyodiktir. Quasikristalleri keşfeden Dan Shechtman bu keşfiyle 2011 yılında Nobel Kimya Ödülü’nü kazandı.

Siz de farklı renklerdeki kartonları Penrose parçaları şeklinde kesip Penrose mozaikleri oluşturabilirsiniz.