Sıfır Faktöriyel Neden Bire Eşittir?
Lise yıllarında tanıştığımız faktöriyel kavramını hepimiz hatırlarız. Sayının sağına ünlem konularak gösterilen faktöriyel işareti, permütasyon ve kombinasyon konularının temelidir. Peki bu konuda öğrendiğimiz sıfır faktöriyel ifadesi neden bire eşittir?
Çizim: Umut Aybek
Permütasyon, belirli sayıda birbirinden farklı nesnelerin kaç farklı şekilde sıralanacağıyla ilgilenir. Kombinasyon kavramı ise nesnelerin sıralamasıyla değil sadece seçimiyle ilgilenir.
Bu konuları öğrendiğimiz sırada ezberleyip sorularda kullandığımız bir eşitlik vardır: 0!=1. Fakat bu eşitlik hep kafamızı karıştırır. Gelin şimdi kafa karışıklığına yol açan bu durumun açıklamasını öğrenelim.
Öncelikle sıfır faktöriyelin tanım gereği bire eşit olduğunu söylemeliyiz. Yani aslında 0! =1 ifadesi ispatlanabilen bir eşitlik değildir. Bu ifade ispatlanamasa da neden doğru olarak kabul edildiği açıklanabilir. Bunun için faktöriyel kavramının tanımını hatırlayalım:
Tanım: 1’den büyük bir n doğal sayısı için, 1’den n’ye kadar olan doğal sayıların çarpımına n faktöriyel denir ve n! ile gösterilir.
Örneğin 3! ifadesi 1.2.3 çarpımına, 4! ifadesi ise 1.2.3.4 çarpımına eşittir.
Kombinasyon hesabında kullandığımız formül ise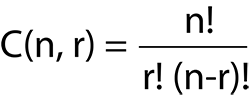 
şeklindedir. Buradaki “n” kümenin toplam eleman sayısı, “r” ise seçilen elemanların sayısıdır. Seçilen elemanların hangi sırada seçildiği önemli değildir.
Örneğin bize “5 kişilik bir ekipten 3 kişi kaç farklı şekilde seçilebilir?” şeklinde bir soru sorulduğunda cevabın 5’in 3’lü kombinasyonuna eşit olduğunu biliriz: C(5,3). Yani 5 kişilik bir ekipten 3 kişi 10 farklı şekilde seçilebilir.
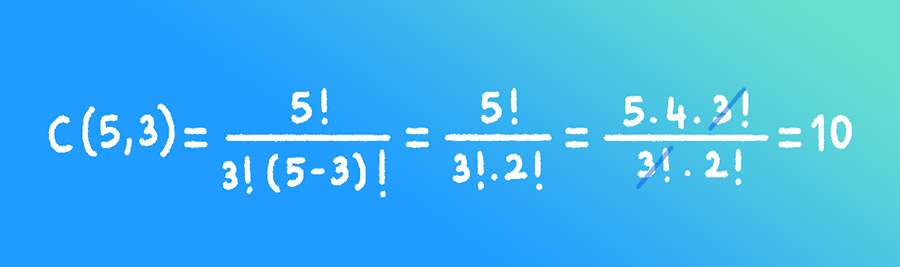
“5 kişilik bir ekipten 5 kişi kaç farklı şekilde seçilebilir?” sorusunun cevabı içinse elimizde tek bir seçenek mevcuttur. Çünkü ekipte zaten 5 kişi yer alıyor ve biz hepsini seçiyoruz. Kombinasyon hesabındaki formülü kullandığımızda ise 0! ifadesiyle karşılaşırız.
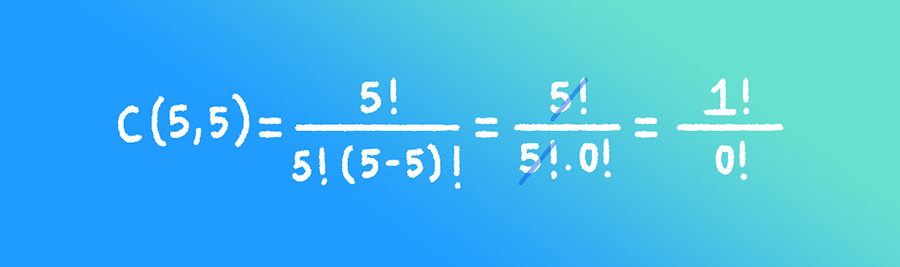
Bu durumda, 5’in 5’li kombinasyonunun 1’e eşit olması için 0! ifadesinin çarpma işlemine göre etkisiz eleman olması gerekir. Bu nedenle de 0! ifadesi 1’e eşittir.
Peki 1,2 veya 1,5 gibi ondalık sayıların faktöriyeli hesaplanabilir mi?
Yukarıdaki faktöriyelin tanımı birden büyük tam sayılar için geçerli. Yani sadece bu tanımı göz önüne aldığımızda ondalık sayıların faktöriyelinin hesaplanması mümkün değil. Ancak 1729 yılında ünlü matematikçi Leonhard Euler tarafından keşfedilen ‘’gama fonksiyonu’’ ile ondalık sayıların da faktöriyelleri hesaplanabiliyor. Yani gama fonksiyonu, faktöriyel kavramını karmaşık sayılar ve ondalık sayılar için genelleyen bir fonksiyondur.
Siz de ondalık sayıların faktöriyellerini hesaplamak isterseniz gama fonksiyonunu kullanabilirsiniz.
Kaynaklar:
