Sınırsız Evren ve Genişleme

Yirminci yüzyıldan önce evrenin statik olduğu düşüncesi hâkimdi. Ancak 1920’lerde Edwin Hubble tarafından yapılan gözlemler, evrenin genişlemekte olduğunu gösterdi.

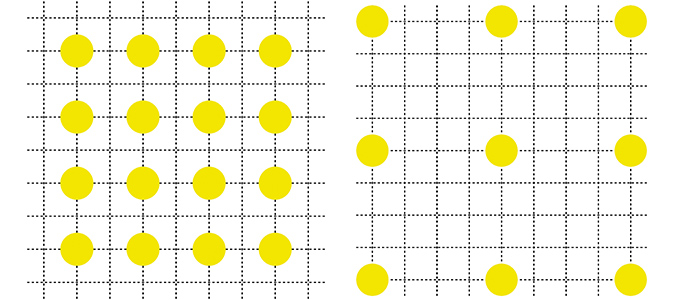
Evrenin genişlemesinin ne anlama geldiği kısaca şu şekilde özetlenebilir. Aralarında çok büyük mesafeler olan iki cisim olsun. Zaman içerisinde evrenin genişlemesi sonucunda cisimler arasındaki mesafe artacak ancak cisimlerin boyutları değişmeyecektir. Bu durumu daha iyi anlamak için Brian Greene’in Evrenin Dokusu isimli kitabında yer alan aşağıdaki betimlemeyi ele alalım. İki boyutlu bir uzay için çizilen bu grafiklerdeki içi dolu diskler makroskobik gökcisimlerini -örneğin gökadaları- kesikli çizgilerse iki nokta arasındaki mesafeyi ölçmek için kullanılabilecek ölçek çizgilerini gösteriyor. Başlangıçta (soldaki grafik) gökadalar arasındaki mesafe daha kısa, ancak zaman ilerledikçe (sağdaki grafik ) gökadalar arasındaki mesafe artıyor. Ancak çizimde gösterildiği gibi evrenin genişlemesi gökadaların boyutlarını (uzayda kapladıkları alanı) değiştirmiyor. Bu durumun nedeni gökadaları oluşturan gökcisimlerini bir arada tutan kuvvetlerdir.

Evrenin genişlemesiyle ilgili diğer bir önemli nokta bu genişlemenin herhangi bir merkezinin olmamasıdır. Samanyolu’ndan baktığımız zaman her yöndeki uzak gökcisimlerinin zamanla daha çok uzaklaştığını görüyoruz. Ancak bu uzaklaşma belirli bir merkezden dışa doğru değildir. Örneğin Andromeda Gökadası’ndan baksaydık yine her yöndeki uzak gökcisimlerinin zamanla daha çok uzaklaştığını görürdük. Genişlemeyi açıklamak için verilen yukarıdaki çizimde de bu durum görülebilir. Betimlenen uzayın hangi noktasında olursanız olun tüm gökadalar zamanla uzaklaşmaktadır, uzayın bir merkezi yoktur.

Evrenin genişlemesi akıllara şu soruyu getirir: Evren neyin içine genişliyor? Örneğin evren küre biçimli bir hacmi kaplıyorsa, bu hacmin dışında ne vardır? Bu ve benzeri soruları tartışmadan önce uzayın eğriliği konusunun ele alınması gerekir. Çünkü genel görelilik kuramı kütlenin uzayı büktüğünü söyler. Dolayısıyla genişleyen uzayın büyük ölçekteki yapısı da evrendeki madde dağılımı tarafından belirlenir.

Evrenin büyük ölçekteki yapısını doğru olarak betimleyecek bir modelin gözlemlerle uyum içinde olması gerekir. Dolayısıyla öncelikle genişleyen evrenle ilgili önemli bir bilgiyi not edelim: Her ne kadar küçük ölçeklerdeki madde dağılımı düzensiz olsa da büyük ölçeklerdeki madde dağılımı homojendir. Yakın çevremize baktığımızda maddenin belirli bölgelerde yoğunlaşarak yıldızları, gezegenleri, gökadaları oluşturduğunu ve bu bölgeler arasındaki madde yoğunluğununsa çok daha düşük olduğunu görürüz. Ancak evren daha büyük ölçeklerde gözlemlendiğinde yıldızların, gezegenlerin ve gökadaların uzaya homojen bir biçimde dağıldığı görülür. Bu durum uzayın büyük ölçekteki eğriliğinin belirli bir anda konumdan bağımsız olduğu anlamına gelir. Evrenin büyük ölçekteki yapısının nitel özelliklerini belirleyecek olansa eğriliğin pozitif mi, negatif mi yoksa sıfır mı olduğudur?

Öncelikle eğriliğin pozitif olduğu durumu ele alalım. İçinde bulunduğumuz üç boyutlu uzayın pozitif eğriliğe sahip olması durumunu betimlemek zordur. Ancak eğer iki boyutlu uzayda yaşıyor olsaydık, uzayın şekli küreye benzerdi (bkz. aşağıdaki şekil).

Bu uzay sonlu olmasına rağmen sınırsızdır. Kürenin üzerindeki hangi noktada olursanız olun herhangi bir yönde hareket edebilirsiniz. Dolayısıyla uzay sınırsızdır. Ancak buna rağmen uzayın sonlu bir alanı vardır.

Bu uzayın bir diğer önemli özelliği belirli bir merkezinin olmamasıdır. Kürenin üzerindeki herhangi bir noktayı merkez olarak seçebilirsiniz, merkez ile merkeze en uzak nokta arasındaki mesafe değişmeyecektir. Kürenin yüzeyine benzeyen iki boyutlu bir uzay zamanla genişlerse, kürenin alanı (uzayın büyüklüğü) artacak ancak üzerindeki cisimlerin boyutları değişmeyecektir.

Örneğin kürenin birbirine zıt iki kutbu üzerinde iki cisim varsa kürenin alanı dört katına çıktığı zaman cisimler arasındaki mesafe iki katına çıkacaktır. Genişlemeyi kürenin üzerindeki hangi noktadan gözlemlerseniz gözlemleyin, her yöndeki uzak cisimlerin giderek daha da uzaklaştığını gözlemlersiniz. Bu durum evrenin istisnasız her yönde genişlediğini gösteren gözlemlerle uyumludur.

Zaman içinde genişleyen iki boyutlu küreye dışarıdan bakan bir gözlemci, bu durumu kürenin zamanla yarıçapının artarak giderek daha büyük hacimleri kapsaması olarak yorumlayabilir. Ancak bu bakış açısı yanıltıcıdır. Çünkü iki boyutlu kürenin üzerinde yaşayan canlılar için kürenin içi ya da dışı diye bir şey yoktur. Küre, uzayın tamamıdır. Dolayısıyla bu uzayın herhangi bir şeyin içinde genişlediği söylenemez.

Uzayın eğriliğinin negatif olduğu durumu betimlemek pozitif olduğu duruma göre çok daha zordur. Böyle bir uzay, küre örneğinde olduğu gibi, daha büyük boyutlu bir uzayın içinde kapalı bir yüzey oluşturmaz. Eğriliğin sıfır olmasıysa uzayın düz olması anlamına gelir.

Peki evrenin büyük ölçekteki eğriliği pozitif midir, negatif midir yoksa sıfır mıdır? Bu sorunun cevabı evrenin ortalama enerji yoğunluğunun ölçülmesiyle bulunabilir. Eğer evrenin ortalama enerji yoğunluğu, kritik enerji yoğunluğu olarak adlandırılan bir değerin üzerindeyse eğrilik pozitiftir, altındaysa eğrilik negatiftir. Ortalama enerji yoğunluğunun kritik enerji yoğunluğuna eşit olmasıysa evrenin büyük ölçekte düz olduğu anlamına gelir. Bugüne kadar yapılan ölçümler, evrenin enerji yoğunluğunun kritik yoğunluğa -deneysel hata oranları içerisinde- eşit olduğunu, yani evrenin düz olduğunu gösteriyor. Sınırsız ve düz bir uzay deyince gözümüzde canlanan ilk şey, her yönde sonsuza kadar uzanan bir uzaydır. Ancak sonsuz büyüklükteki uzay, düz ve sınırsız uzayların tek örneği değildir. Bir uzayın sınırsız ve düz olmasına rağmen sonlu büyüklükte olması mümkündür.  Örneğin konumların iki açıyla (iki periyodik koordinatla) tanımlandığı torus (bkz. yukarıdaki çizim) sonlu büyüklüktedir, sınırsızdır ve düzdür. Bu uzay esasen pürüzsüz, düz bir masanın yüzeyi gibidir. Ancak koordinatlar periyodik olduğu için uzayın bir sınırı yoktur. Sürekli aynı yönde hareket eden bir gözlemci, masanın bir tarafından çıkarken diğer tarafından geri girer.