Sihirli Kareler
1’den 9’a kadar olan sayıları sadece birer kez kullanarak, tüm satır ve sütunlar ile köşegenlerde bulunan sayıların toplamı eşit olacak şekilde 3x3’lük bir kare oluşturabilir misiniz?
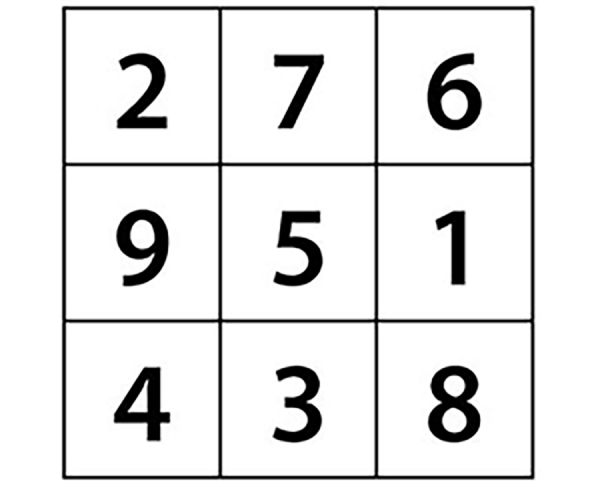
Lo shu karesi
3x3’lük bir kareye 1’den 9’a kadar olan sayılar görseldeki gibi yerleştirildiğinde ‘’3’lü sihirli kare’’ elde edilir. Görseldeki 3’lü sihirli kareye Lo shu karesi de denir. Bu kareye sihirli kare denmesinin nedeni, sayıların belirli bir düzene göre dizilmesidir. Lo shu karesinin tüm satır ve sütunları ile köşegenlerinde bulunan sayıların toplamı hep aynı sayıya yani 15’e eşittir.
Efsaneye göre ‘‘Lo nehri yazısı’’ anlamına gelen Lo shu karesini MÖ 23. yüzyılda Antik Çin’de Kral Yu’nun Lo Nehri’ndeki bir kaplumbağanın kabuk deseninde gördüğü rivayet edilir.
Lo shu karesinden başka ‘’3’lü sihirli kareler’’ de vardır. Lo shu karesini merkezi etrafında 90°, 180° ve 270° döndürdüğümüzde elde ettiğimiz kareler de birer sihirli karedir. 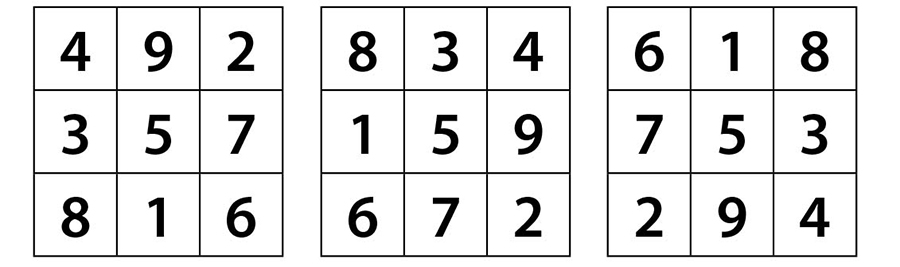
Ayrıca, Lo shu karesi ve döndürülmüş Lo shu karelerinin ayna yansımaları da birer sihirli karedir ve toplamda sekiz adet 3’lü sihirli kare bulunur.
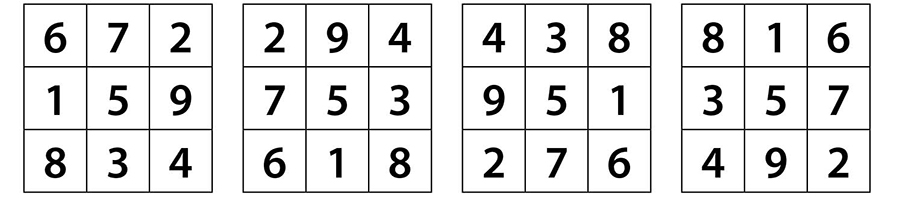
Peki, 3’lü sihirli karelerden başka sihirli kareler var mı?
Cevabımız “evet”. Sihirli kareler bir kenarda bulunan hücre sayısına göre isimlendirilir ve her bir kenardaki hücre sayısı artırılarak daha büyük dereceli sihirli kareler oluşturulabilir. Örneğin 4’lü, 5’li ve n’li sihirli kareler gibi... Sihirli karelerin derecesi büyüdükçe o derece için sihirli kare sayısı da artar. Fakat belirli bir derece için kaç farklı sihirli kare bulunduğunu veren bir formül ise bulunmuyor.
Sihirli kareler, kenarlardaki hücre sayısının tek veya çift oluşuna göre de isimlendirilebilir. Örneğin 4’lü sihirli karenin ‘’çift sihirli kare’’ ve 5’li sihirli karenin ‘’tek sihirli kare’’ olarak adlandırılması gibi...
Bir n’li sihirli kare, 1’den n2’ye kadar olan farklı tam sayıların kare şeklinde dizilmesiyle oluşur. Öyle ki karenin tüm satır, sütun ve köşegenlerinde bulunan sayıların toplamı birbirine eşittir. Bu karede bulunan tam sayıların toplamı 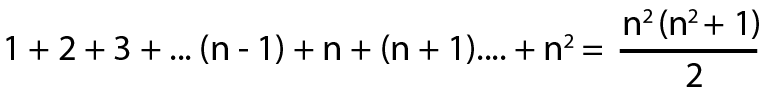 ’dir. Yine bu karede toplamda n tane satır veya sütun olduğu için her bir satırdaki veya sütundaki sayıların toplamı
’dir. Yine bu karede toplamda n tane satır veya sütun olduğu için her bir satırdaki veya sütundaki sayıların toplamı 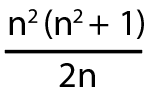 formülüyle bulunur. Örneğin 5’li sihirli karedeki tüm sayıların toplamı 325’e ve bu karenin her bir satır, sütun ve köşegeninde bulunan sayıların toplamı 65’e eşittir.
formülüyle bulunur. Örneğin 5’li sihirli karedeki tüm sayıların toplamı 325’e ve bu karenin her bir satır, sütun ve köşegeninde bulunan sayıların toplamı 65’e eşittir.
Peki, 5’li sihirli kareyi nasıl oluşturabiliriz?
Öncelikle 5’li bir sihirli kare oluşturmak için birçok farklı yöntem kullanılabilir. Bizim kullanacağımız yöntem ise bunlardan sadece biri.
1 sayısını karenin en üst sırasının tam ortasındaki hücreye yerleştirerek başlayalım.

Sonraki sayıları eğer yer varsa bir önceki sayının hep sağ üst çaprazındaki hücreye yazalım. Ancak 1’den sonra 2 sayısı için sağ üst çaprazda yer olmadığından, 2’yi sağdaki sütunun en altındaki hücreye yerleştirelim. Burada sihirli karenin en üst satırdan sonra en alttaki satır ile devam ettiğini düşünebiliriz. Daha sonra 3 sayısını 2’nin sağ üst çaprazındaki hücreye yazalım.
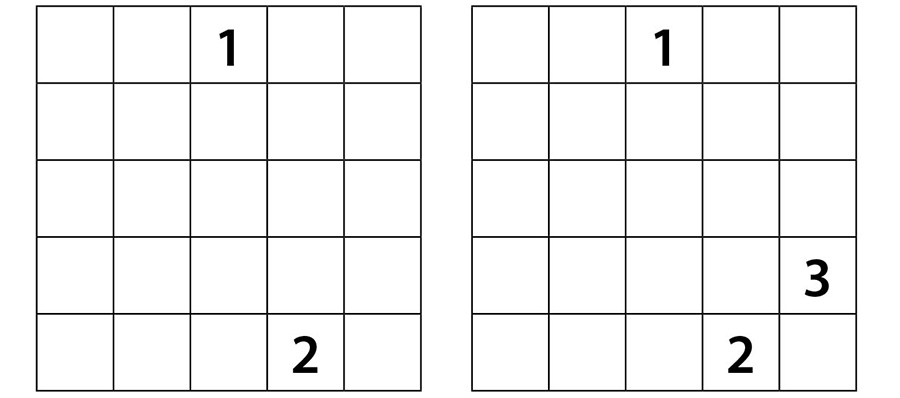
Şimdi 4 sayısını yerleştirmeliyiz fakat 3’ün sağ üst tarafında yerimiz yok, karenin dışına çıkıyoruz. Bu durumda sağdaki son sütundan sonra soldaki ilk sütun devam ediyormuş gibi düşünebilir ve 4’ü şekildeki gibi yerleştirebiliriz.
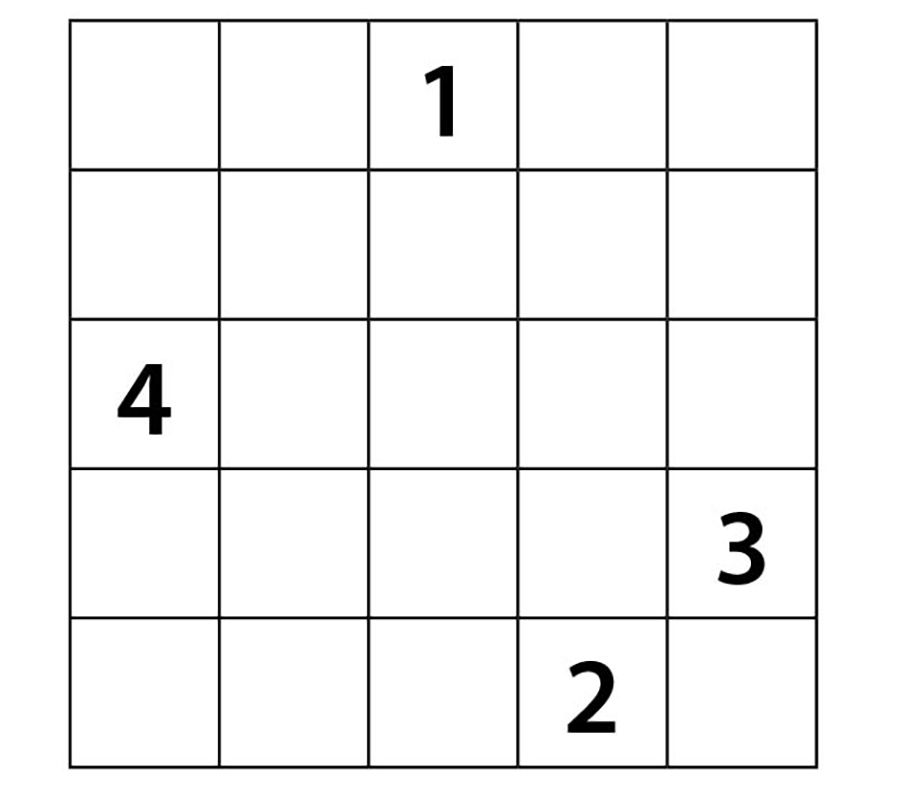
5 sayısını ise 4’ün sağ üst çaprazına yerleştirdiğimizde aşağıdaki gibi bir kare elde ederiz.
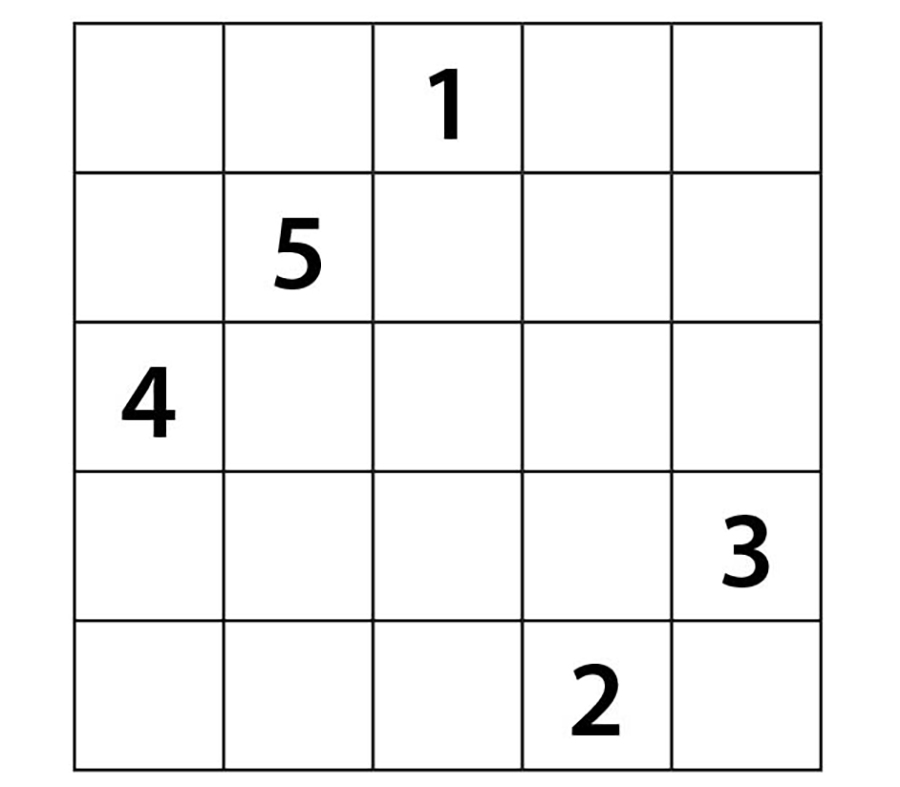
6 sayısını 5’in sağ üst çaprazına yazamayız çünkü orada 1 sayısı var. Böyle bir durumda yeni sayımız bir önceki sayının hemen altında yer almalı. Yani 6 sayısını 5’in altına yazalım.
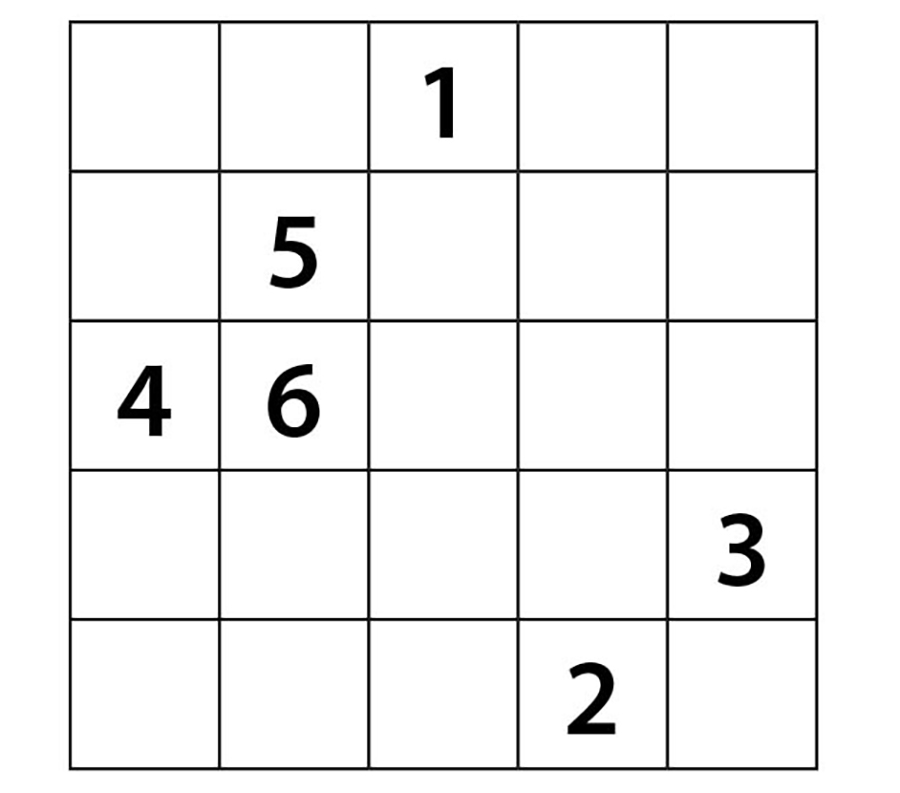
Artık diğer sayıları nasıl yerleştireceğimizi biliyoruz. 7 sayısını 6’nın sağ üst çaprazına, 8’i ise 7’nin sağ üst çaprazına yerleştirelim.
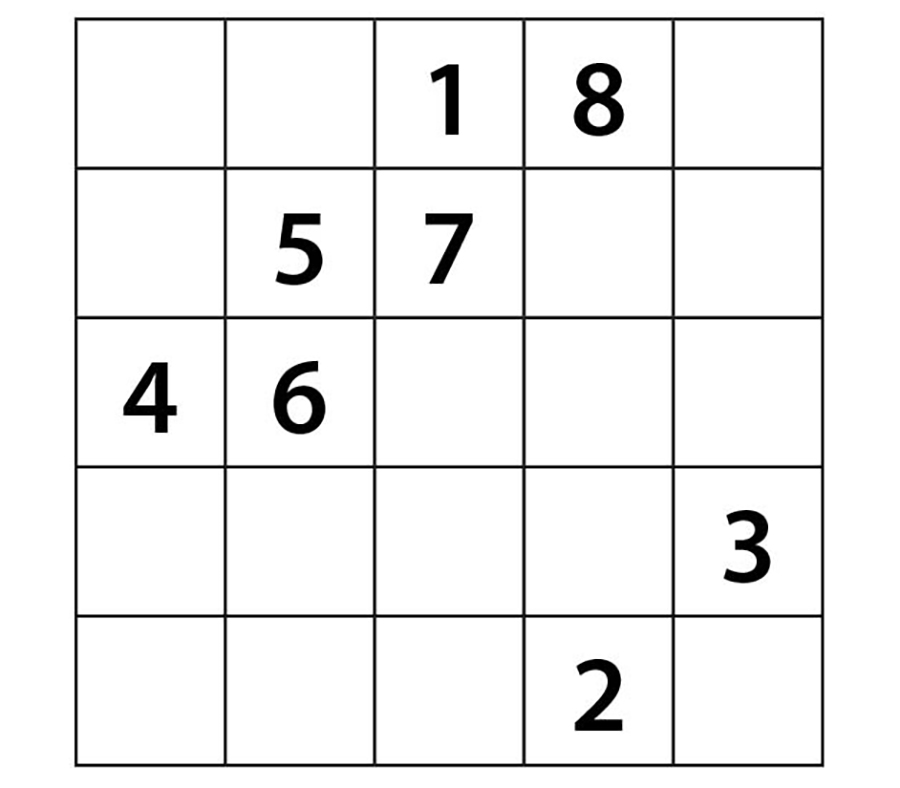
9 sayısını 8’in sağ üst çaprazında hücre bulunmadığı için son sütunun en alt satırına yazalım. Aynı şekilde 9’un sağ üst çaprazında yer olmadığı için 10 sayısını ilk sütunun dördüncü satırına yerleştirelim.
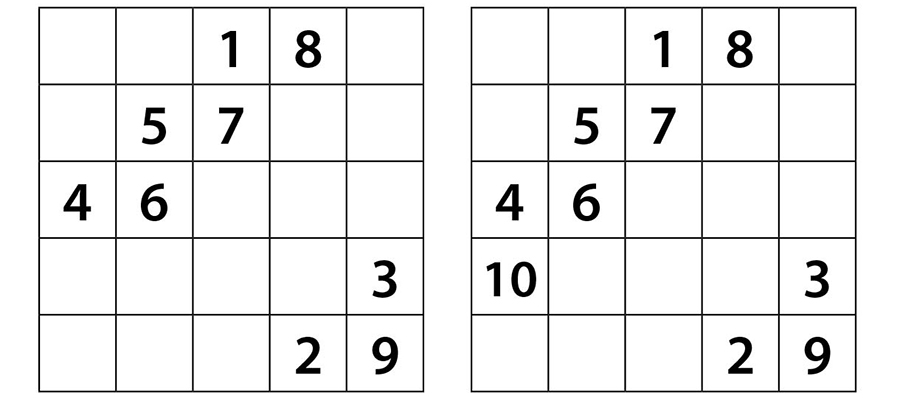
11 sayısını 10’un sağ üst çaprazına yazamayız. O yüzden 11 sayısını 10’un hemen altındaki hücreye yazalım. Diğer sayılarımızı sırasıyla bir önceki sayının sağ üst çaprazındaki hücreye yerleştirelim.
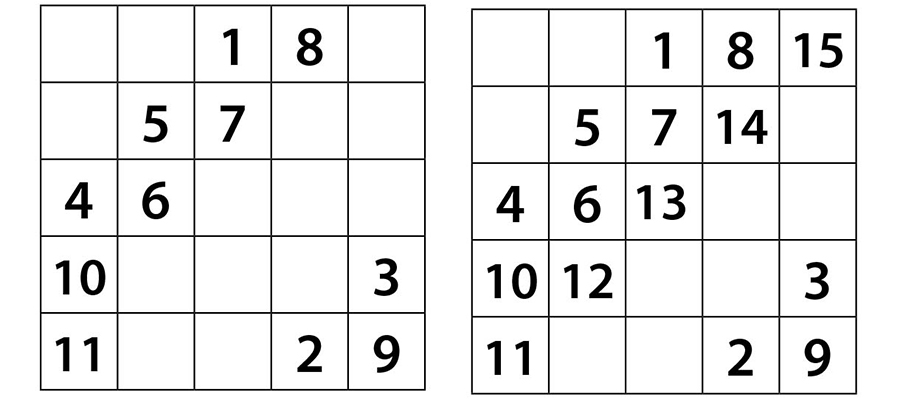
16 sayısını yazmamız gereken yerde 11 sayısı olduğu için 16 sayısını 15’in hemen altına yazalım. Daha sonra 17, 18, 19 ve 20 sayılarını önceki sayılarda olduğu gibi yerleştirelim.
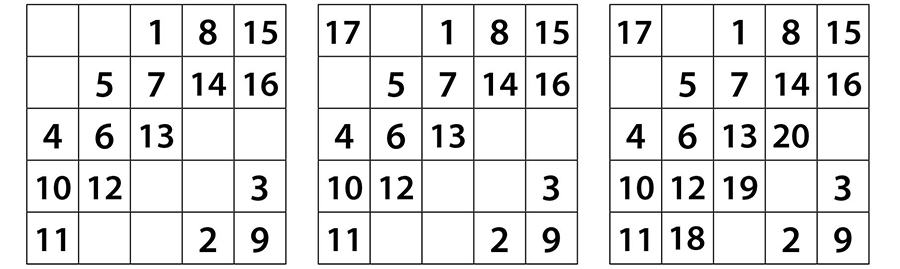
21 sayısını 20’nin hemen altındaki hücreye yazmamız gerektiğini biliyoruz. 22 sayısını da 21’in sağ üst çaprazına yazalım.
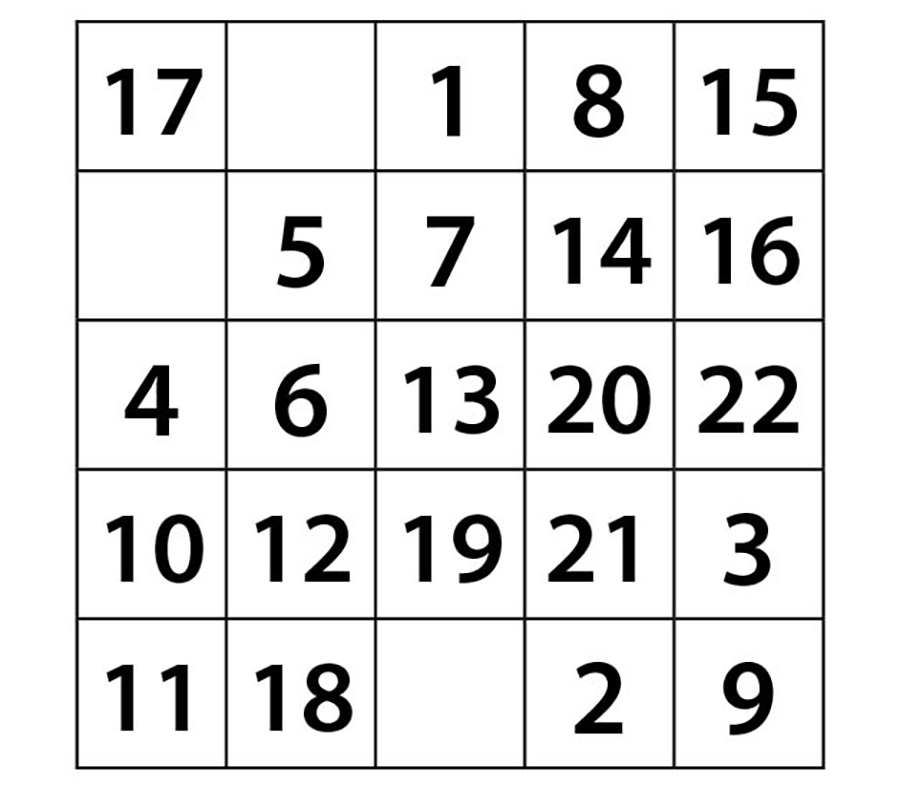
Son üç sayımızı da yerleştirdiğimizde 5’li sihirli karemizi oluşturmuş oluruz.
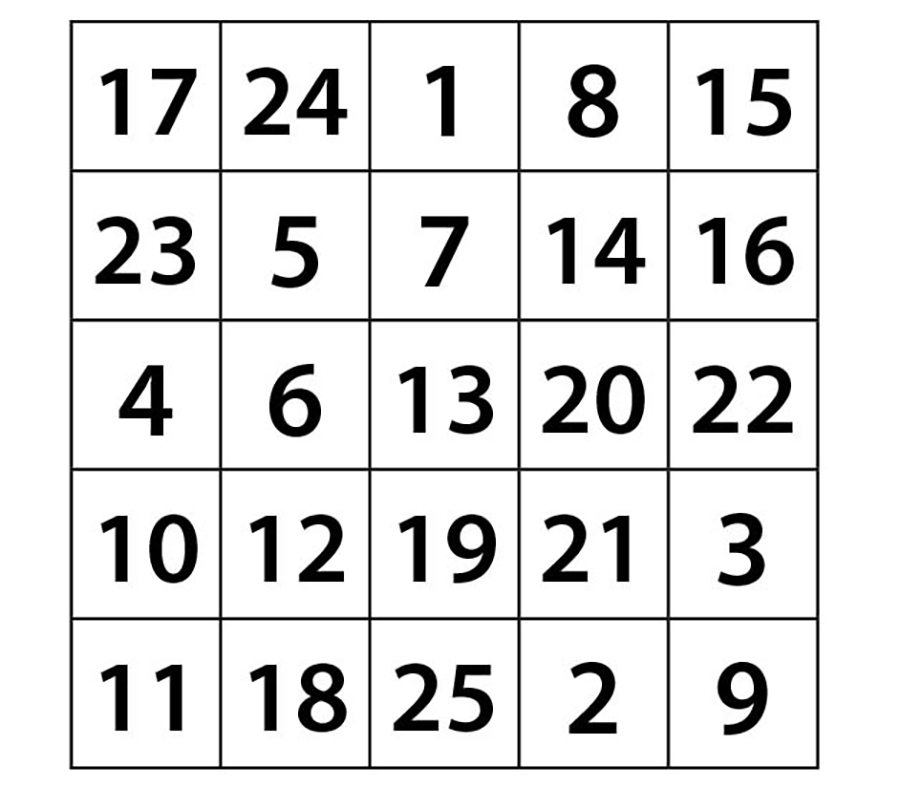
Oluşturduğumuz 5’li sihirli karenin merkezine eşit uzaklıkta olan karşılıklı hücrelerdeki sayıların toplamlarının, birbirlerine ve merkezde bulunan sayının iki katına eşit olduğunu fark etmişsinizdir.
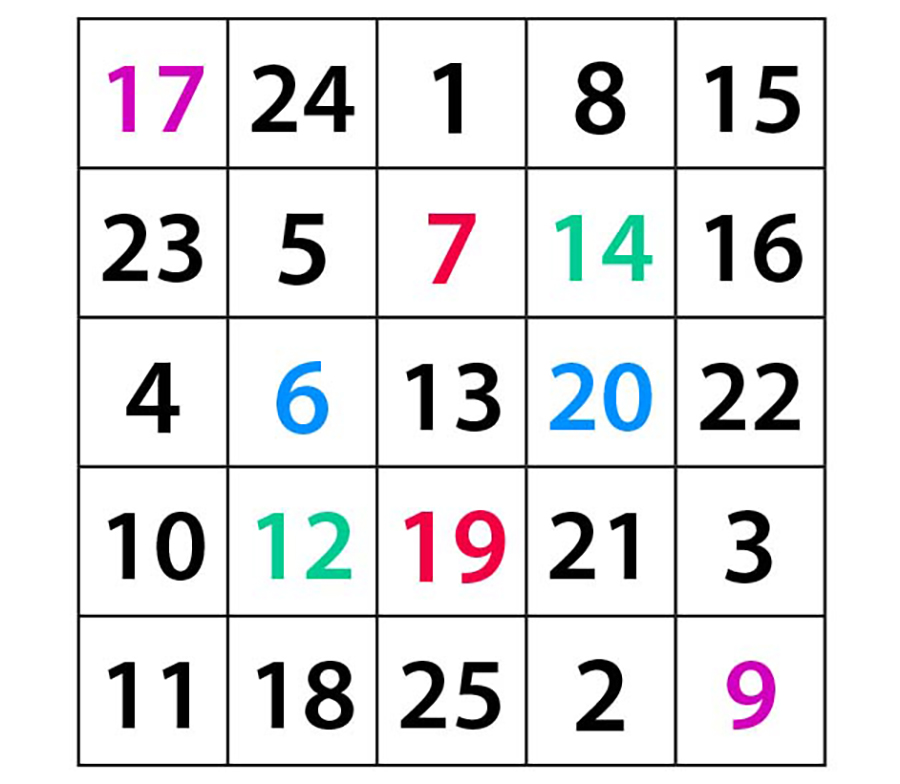
Araştıralım!
5’li sihirli karemizi oluşturmak için izlediğimiz yöntemle tek sihirli karelerin tümünü oluşturabiliriz. Fakat 4’lü, 6’lı ve 8’li gibi çift sihirli kareleri bu yöntemle oluşturamayız. Çift sihirli karelerin nasıl oluşturulacağını da kendiniz araştırarak öğrenebilirsiniz.
Kaynaklar: