Çizge Kuramı ile Biyometrik Veriyi Nasıl İşleriz?

Günlük hayatta karşılaştığımız problemler (örneğin bir şirketin çalışma şemasının oluşturulması ya da bulaşıcı bir hastalığın nasıl yayıldığının anlaşılması) genellikle çok katmanlı ve karmaşıktır. Bu nedenle bu tür problemler doğrusal yöntemlerle değil, sistemi analiz edebilmemizi sağlayan ağ yaklaşımı ile çözülebilir. Çizge kuramı, ağ şeklinde modellenebilen problemlerin çözümünde bize yardımcı olabilir. Gelin şimdi çizge kuramının nasıl ortaya çıktığını ve bu kuramın günlük hayatta parmak izi tespiti ve yüz tanıma gibi biyometrik verilerin incelenmesinde nasıl kullanılabileceğini inceleyelim.

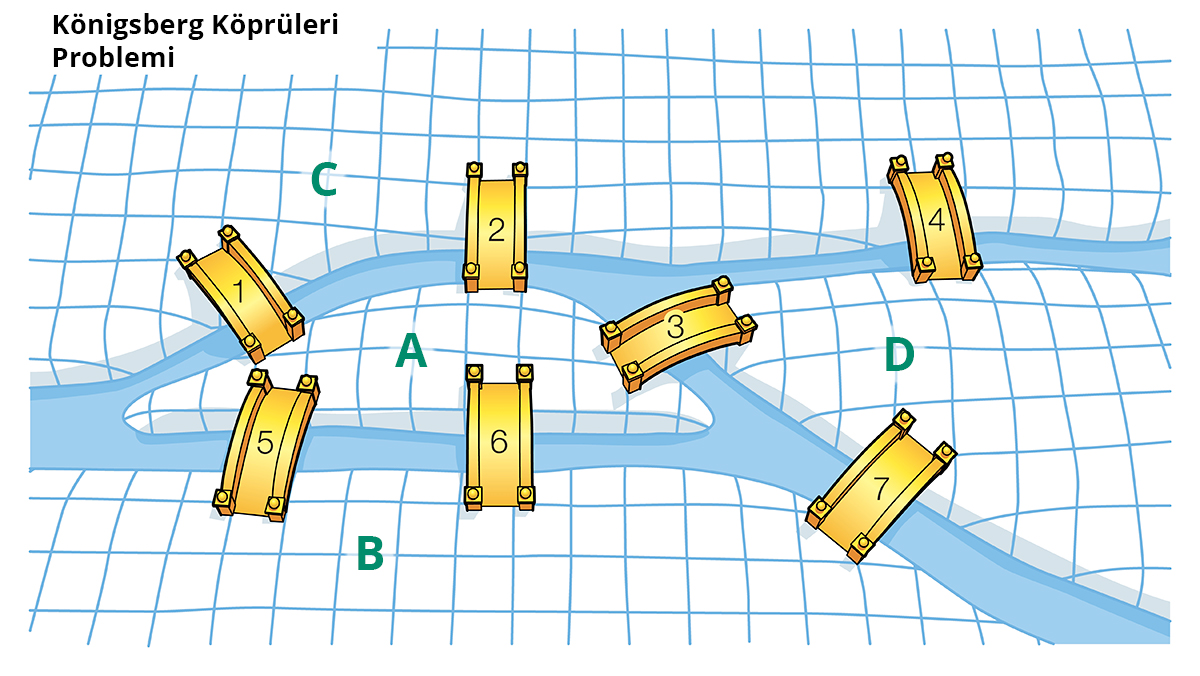
Çizge kuramı, ünlü matematikçi Leonhard Euler’e 1736’da bir mektup ile yöneltilen Königsberg köprüleri problemi ile doğdu. Problemde bugün Kaliningrad olarak adlandırılan Königsberg şehrinin dört bölgesini birbirine bağlayan, Pregel Nehri’nin üzerindeki yedi köprüden sadece birer kez geçerek tüm bölgeleri ziyaret edip başlangıç bölgesine ulaşmayı sağlayan bir rota çizilmesi gerekiyordu. Bu sayede posta gibi teslimatlar şehir içinde en verimli şekilde yapılabilecekti. Şehrin sakinleri böyle bir yolculuğun mümkün olup olmadığına karar veremeyince Euler’e mektup yazdılar. Euler, Königsberg köprüleri probleminin çözülemez olduğunu gösterdiğinde aynı zamanda matematiğe de yeni bir branş kazandırmış oldu: çizge kuramı.

Aslında bu problem size çocukken oynadığınız bir oyunu anımsatmış olabilir: elinizi kâğıttan hiç kaldırmadan ve çizdiğiniz bir çizginin üzerinden tekrar geçmeden bir ev çizmek. Daha önce hiç oynamadıysanız bu oyunu aşağıda verilen şekil üzerinde deneyebilirsiniz.

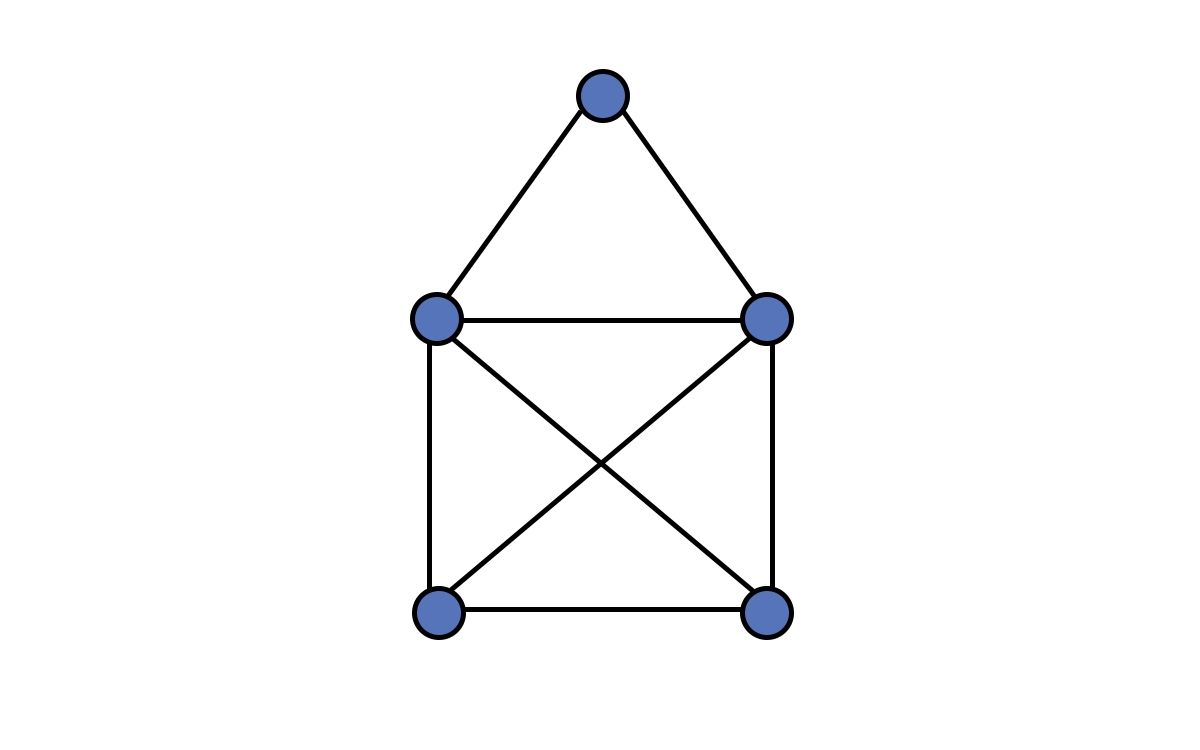
Her iki problemde de çözüm üzerine çalışırken önce köşeleri belirler, daha sonra bu köşeleri çizgiler ile birleştirmeye çalışırız. Çizge kuramının da yapı taşları “düğüm” ve “çizgi”lerdir. Örneğin ev çizme probleminde beş düğüm ve bu düğümleri birleştiren sekiz çizgi var.

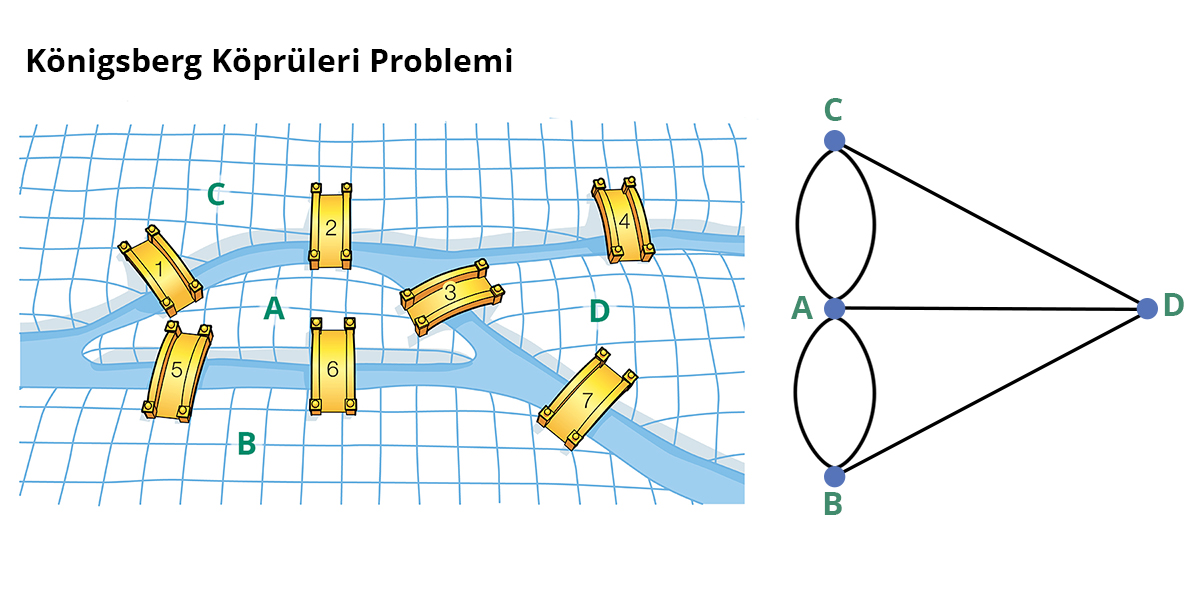
Bu iki terim ile birçok ağı tanımlayabilir, çözemediğimiz problemlere çizge kuramı ile cevap arayabiliriz. Örneğin Königsberg şehrinin bölgelerini birer düğüm, her bir köprüyü de bu düğümleri birleştiren çizgiler olarak kabul edersek, verilen problem için şöyle bir çizge oluşturabiliriz:

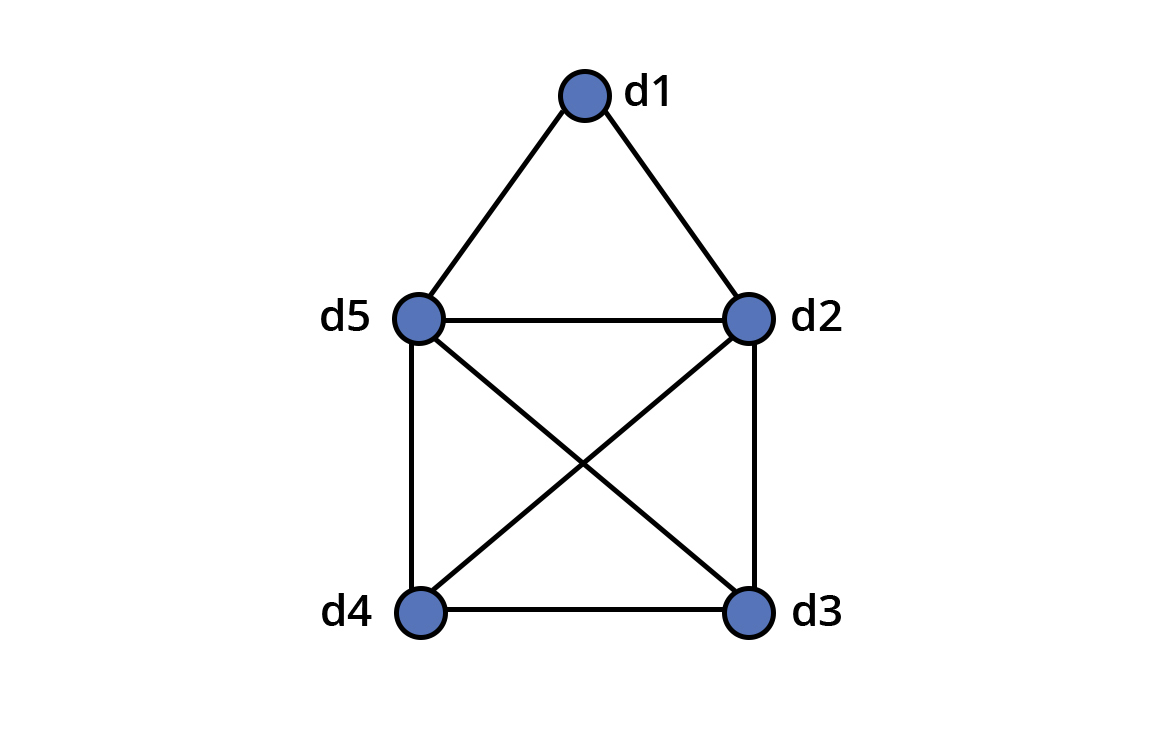
Çok daha basit bir örnek verelim. Vücudumuzu bir ağ gibi düşünelim. Beynimizi (d1), akciğerimizi (d2), kalbimizi (d3), dalağımızı (d4) ve kalın bağırsağımızı (d5) birer düğüm olarak kabul eder ve iki düğümün arasında çizgi oluşturmayı da “organların komşu olması” şeklinde tanımlarsak şu çizgeyi oluşturabiliriz:

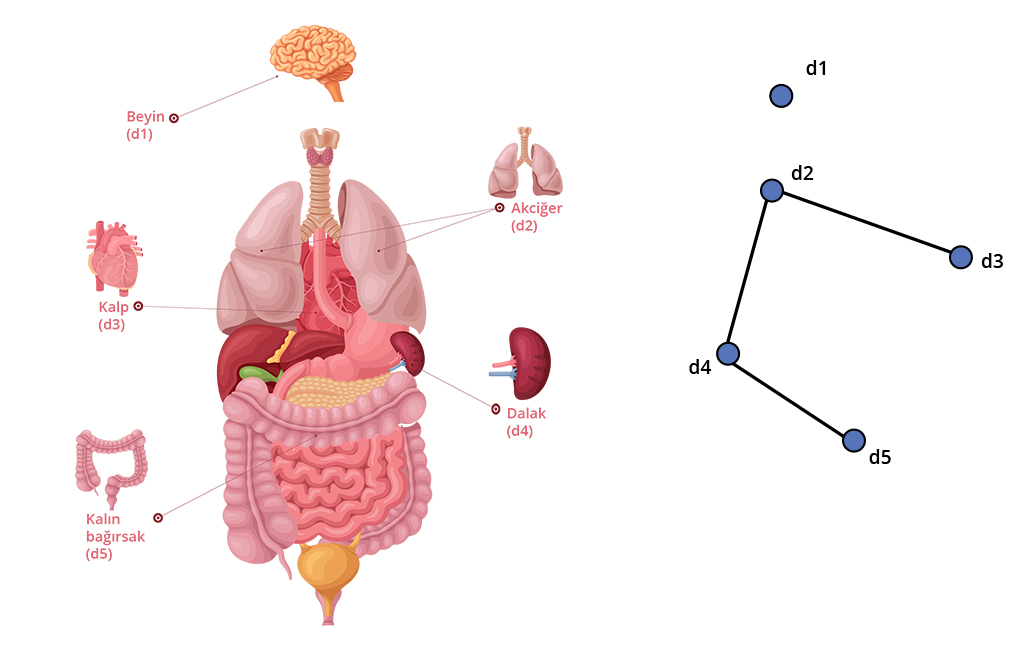
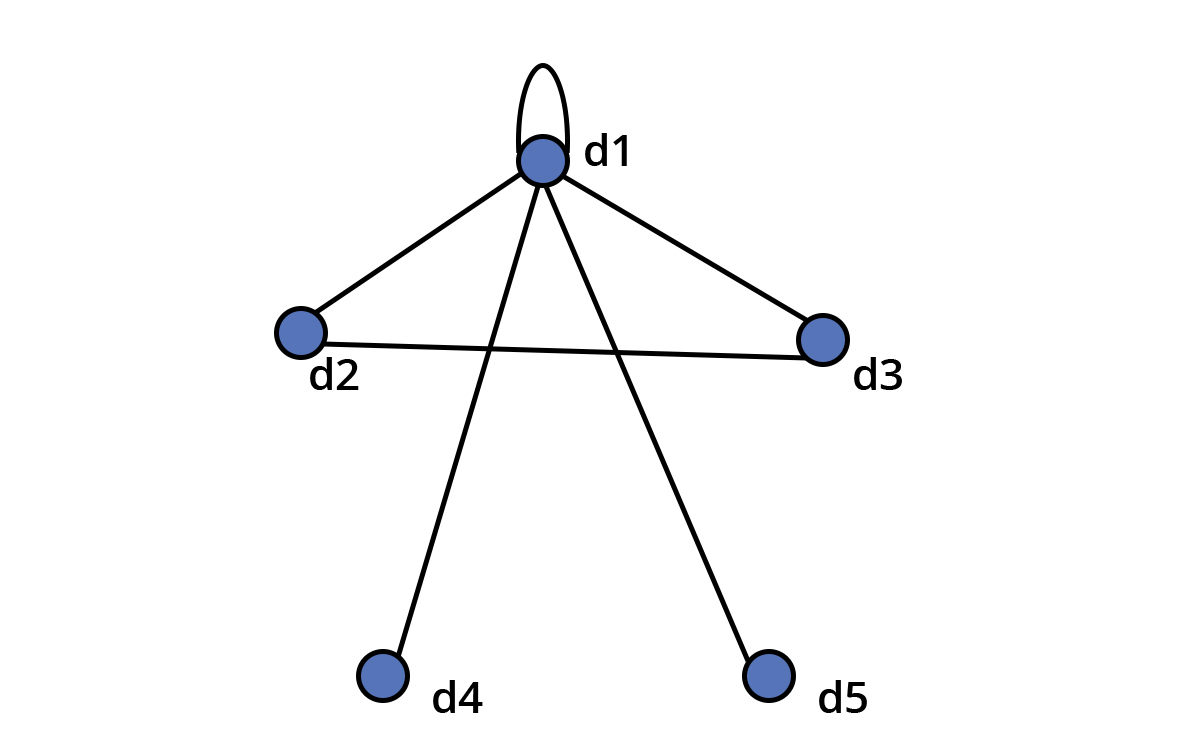
Eğer çizgedeki düğümler arası çizgileri, “organların damar ya da sinir ile doğrudan bağlantılı olması” şeklinde tanımlasaydık ortaya daha farklı bir çizge çıkardı. Beynin kendi içinde farklı bölümleri olduğunu ve bu bölümlerin birbiri ile bağlantılı olduğunu düşünürsek aslında d1 düğümünün kendisi ile de çizge oluşturduğunu görebiliriz.

Euler’in temelini attığı çizge kuramının daha sonra çeşitli alt dalları doğdu. Königsberg köprüleri probleminde olduğu gibi birçok çizge uygulamasında çizgilerin uzunlukları veya yönleri önemli değildir. Çizge sadece iki düğümün ilişkili olduğunu gösterir. Ama bazen ağ şemalarında, örneğin internette farklı paydaşlar arasındaki veri akışında, çizgilerin yönlerinin belirtmesi daha karmaşık problemlerin çözülmesini sağlar. Çizge kuramı mühendislik, tıp, ekonomi, ticaret gibi birçok alanda uygulaması olan kapsamlı bir konudur.

Biyometrik Veri Analizinde Çizge Kuramı

Parmak izi tespitinde, parmak izleri çizgeye dönüştürülerek eşleme yapılabilir. Bir kişinin parmak izini, geometrik şekillerden oluşan bir görsel olarak düşünebileceğimiz gibi parmak izindeki belirlenen noktalar ile oluşturulacak bir ağ şeması olarak da düşünebiliriz. Çizge kuramının biyometrik veri analizinde kullanıldığı başka bir örnek de yüz tanımadır. Örneğin ben kendi fotoğrafımda görsel biyometrik verileri matematiksel verilere dönüştürerek yüzümün bir çizgesini oluşturabilirim ve başka çizgeler (örneğin abimin yüzünün çizgesi) ile karşılaştırabilirim. Yüzümde belirlediğim noktaları bir düzene göre birleştirdiğim bu çizgede, her bir çizginin uzunluğunu bilirsek yüz eşleme için tutarlı sonuçlar elde edebiliriz.

Başka bir ülkeyi ziyaret ettiğimizde o ülkeye girişte kimlik doğrulama aşamasında yüz tanıma teknolojisi kullanılır. Örneğin en son Hollanda'yı ziyaret ettiğimde ülkeye girişte, polis memuru pasaportumu okuttuktan sonra fotoğrafımı çekti. Kullandığı bilgisayarda pasaportta tanımlı olan fotoğraf ile çekilen fotoğrafı eşleştirdi ve kimliğimi doğruladı. Bu nedenle pasaport gibi belgelerde belirli standartlar çerçevesinde çekilen biyometrik fotoğraflar kullanılır.

Siz beni biyometrik olmayan, gülümsediğim bir fotoğraf ile tanıyın diye buraya gülümsediğim bir fotoğraf ve çizgesini bırakıyorum. Bir gün yolda karşılaşırsak, beyninizde bu fotoğraftan dolayı oluşan imge ile beni gördüğünüzde zihninizde canlanan imgeyi eşleştirip bana “Merhaba!” derseniz tanışır, sohbet ederiz.

Okuma Önerileri:

• https://www.csoonline.com/article/3339565/what-is-biometrics-and-why-collecting-biometric-data-is-risky.html
• https://readwrite.com/2020/03/12/history-of-facial-recognition-technology-and-its-bright-future
• https://www.comap.com/undergraduate/projects/biomath/PDF/Crime_And_Forensics_SE.pdf
• https://www.herkesebilimteknoloji.com/yazarlar/lale-akarun/yuz-tanima-hayati-kolaylastiran-bir-teknoloji-mi-ozel-hayatimiza-mudahale-mi
• https://onin.com/fp/fphistory.html
• https://bilimteknik.tubitak.gov.tr/system/files/makale/cizge.pdf