GeoGebra ile Katı Cisimler

Matematiğin zevkine varan insanlar için matematik, içinde bulunduğu çevreyi anlamak ve kavramak için daima bir kaynak olmuştur. Bilim ve teknolojinin son yıllardaki olağanüstü gelişimiyle beraber hayatımıza giren bilgisayar ve benzeri teknoloji ürünleri, öğrenme materyallerinin görselleşmesini ve böylece öğrenimin kolaylaşmasını, zevkli hale gelmesini, hızlanmasını ve daha kalıcı olmasını sağlamaya başladı.

Öklid geometrisinde bir nesnenin sadece uzunluğu varsa bir boyutlu; uzunluğu ve derinliği varsa iki boyutlu; uzunluğu, derinliği ve yüksekliği varsa üç boyutludur.

Katı cisimleri en genel haliyle belli bir hacme sahip olan şekiller olarak tanımlayabiliriz. Bir şeklin hacminin olması için en, boy ve derinlik bileşenlerinin hepsinin birden var olması yani üç boyutlu olması gerekir. Peki, nelerdir bu katı cisimler? Dikdörtgenler prizması ve küp üç boyutlu geometrik cisimlerin örneklerindendir. Günlük hayatta karşımıza çıkan top, soba borusu, konserve kutuları ve benzeri fiziksel nesneler de üç boyutludur.

Tabanları herhangi bir çokgensel bölge (eşkenar çokgen) ve yan yüzleri dikdörtgensel bölge olan cisimlere dik prizma denir. Bu prizmalarda, tabanları birleştiren yanal ayrıtlar tabanlara diktir. Tabanları düzgün çokgensel bölge olan dik prizmalara düzgün dik prizmalar denir. Prizmalar tabanlarına göre isimlendirilir: üçgen prizma, kare prizma, dikdörtgenler prizması, altıgen prizma, beşgen prizma...

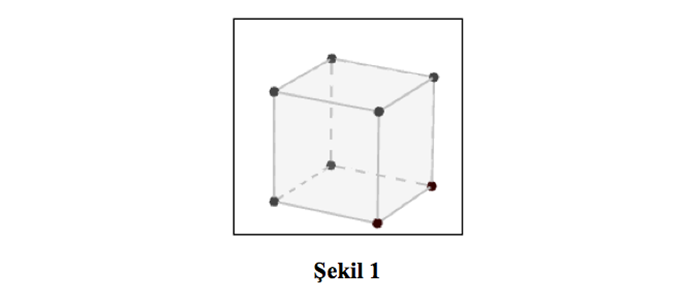
İki boyutlu çizimlere bakarak üç boyutlu cisimleri kavramak zordur. Mesela küp kavramını ele alalım. Hepimiz kolaylıkla bir kâğıdın üzerine küp çizebiliriz (Şekil 1). Peki, iki boyutlu çizimdeki uzunluğu, derinliği ve yüksekliği kavrayarak şeklin üç boyutlu olduğunu anlamak kolay mıdır?

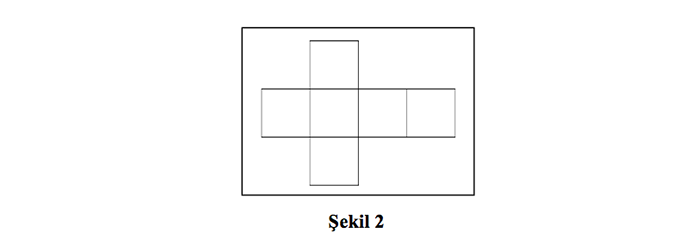
Şimdi küpün açılmış hali olarak aşina olduğumuz altı kareli şekli ele alalım. (Şekil 2). Bu şekle nasıl bir işlem uygulamalıyız ki uzunluğu ve derinliği olan bu iki boyutlu şekli yükseklik de ekleyip üç boyutlu hale getirebilelim? Şekil 2’deki çizimi bir kâğıdın üzerine yaptıktan sonra kâğıdı kesip katlayarak bir küp elde edebiliriz. Fakat bu küpün kenar uzunluklarını değiştirmek veya dörtgen, beşgen, altıgen prizma çizmek istersek ne yapmalıyız?

Tam da bu noktada katı cisimlerin yani piramit, prizma gibi bir hacme sahip geometrik şekillerin daha kolay anlaşılabilmesi için dinamik matematik yazılımları kullanılabilir. Bu yazılımların kullanılmasındaki amaç, kenar uzunlukları ve hatta kenar sayısı değiştiğinde üç boyutlu cisimlerde meydana gelecek değişiklikleri gözlemlemek ve belirlemektir.

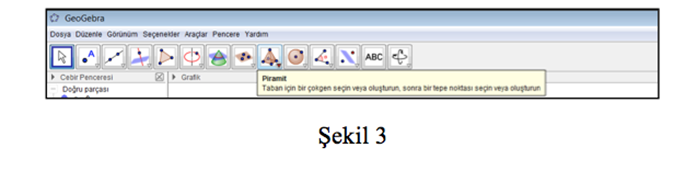
GeoGebra programını kullanarak katı cisimleri çizmek çok kolaydır. Programdaki araç kutucuklarında verilen komutlar sayesinde katı cisimleri nasıl çizeceğimizi kolayca anlayabiliriz. Örneğin piramit çizmek istediğimizde piramit araç çubuğuna gelerek bu katı cismi hangi komutlarla (Taban için bir çokgen seçin veya oluşturun, sonra bir tepe noktası seçin veya oluşturun) çizeceğimizi belirleyebiliriz (Şekil 3).

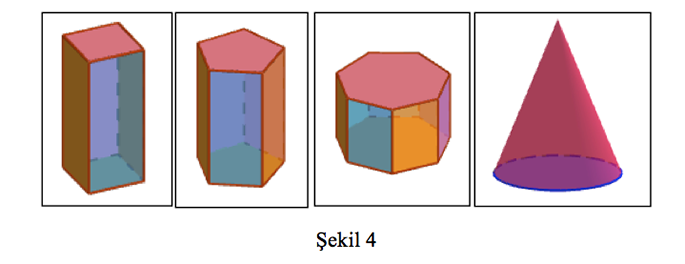
GeoGebra yazılımını kullanarak farklı katı cisimler çizebiliriz (Şekil 4). Bu katı cisimlerin hepsini ayrı ayrı çizebileceğimiz gibi GeoGebra programının en büyük faydalarından biri olan sürgü yardımıyla da çizebiliriz. Sürgü, bize katı cismin öncelikle tabanına ait kenar sayısını bulmamızda yardımcı olabilir. Bu sayede tabandaki kenar sayısını değiştirerek dörtgen, beşgen, altıgen prizma çizebiliriz. Başka bir sürgüyle de katı cismin yüksekliğini ayarlayabiliriz. Kenar sayısında olduğu gibi, herhangi bir katı cismin yüksekliğini de değiştirebiliriz. Bu şekilde sadece bir kenarı ve yüksekliği belli olan sabit bir katı cisim elde etmek yerine, tabanındaki kenar sayısını ve yüksekliğini değiştirebileceğimiz katı cisimler elde edebiliriz. Böylece katı cisim deyince akla sadece Şekil 2’de verilen küpün değil, başka nesnelerinde gelebileceği algısını güçlendirebiliriz.

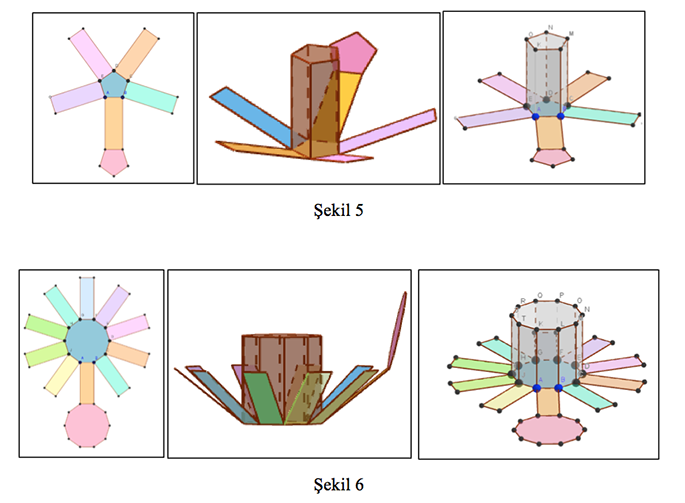
GeoGebra programının etkili özelliklerinden biri olan, katı cisimlerin açık ve kapalı hallerini veren ve nasıl açılıp kapandıklarını gösteren animasyon ile katı cisimlerin açık ve kapalı hallerinin nasıl eşleştiğini gösterebiliriz. Mesela Şekil 1’de verilen küpün açık hali Şekil 2 iken bir beşgen prizmanın açık hali nasıldır? GeoGebra programı ile bunu kolaylıkla gösterebiliriz (Şekil 5). Aynısını sadece beşgen prizma için değil tabandaki kenar sayısını değiştirerek herhangi bir prizma, örneğin ongen prizma, için de yapabiliriz (Şekil 6).

https://www.geogebra.org/m/fx68RtSS?doneurl=%2Fozgecoban

https://www.geogebra.org/m/pGPwMeGv?doneurl=%2Fozgecoban

https://www.geogebra.org/m/Pcr7s4Zv?doneurl=%2Fozgecoban

Görüldüğü gibi anlaşılması çok zor görünen üç boyut ve katı cisim kavramlarının öğretiminde GeoGebra programını kullanmak faydalı olabilir. Özellikle iki boyutlu bir nesnenin üç boyutlu bir nesneye nasıl dönüştüğünü görmek için dinamik matematik yazılımlarının kullanılmasının faydalı olabileceği düşünülüyor. Tabana ait kenar sayısının ve yüksekliğin değişimi ile katı cismin açık ve kapalı hallerinin görselleştirilmesini sağlayan sürgülerden oluşan GeoGebra etkinliğinin nasıl inşa edilebileceğini buradan öğrenebilirsiniz. Piramit ve koninin inşasını, siz sevgili okuyucularımıza bırakıyoruz.