Sonsuz Tane Sayının Toplamı Hesaplanabilir mi?

Sorunun cevabını bulmak için gerçekleşmesi muhtemel çeşitli durumları göz önünde bulundurmamız gerekir. Örneğin ilk atışı yapan 1. kişi hedefi vuramaz ve ardından atış yapan 2. kişi hedefi vurabilir. Ya da ilk atışı yapan 1. kişi hedefi vuramaz, ardından atış yapan 2. kişi de hedefi vuramaz. Sonra tekrar atış yapan 1. kişi hedefi vuramaz ve atış sırası gelen 2. kişi hedefi vurabilir. Gerçekleşmesi muhtemel durumlar bu şekilde devam ettirilir. Her defasında 1. kişinin hedefi vuramaması ve aynı şekilde belirli bir atış sonrası 2. kişinin hedefi vurması gerekir. Buna göre ikinci kişinin oyunu kazanma olasılığı aşağıdaki sonsuz toplama eşittir.

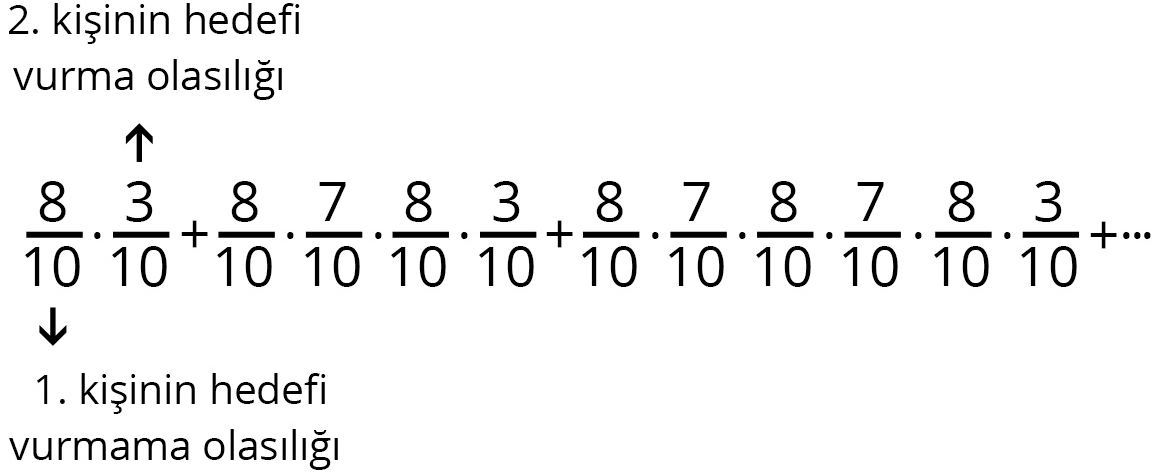
Sorunun cevabı için bu toplamın neye eşit olduğunu bulmamız gerekir. Matematikte sonsuz terimin toplamı kimi zaman sonlu bir sayıya eşit olabilir. Sonsuz toplamın sonlu bir sayıya eşit olduğu en basit örneklerden biri geometrik serilerdir. Buradaki seri kelimesi aslında toplamı ifade eder. Geometrik seriler genel olarak

a+ar+ar²+ar³+ar⁴+...

şeklindeki sonsuz toplamdan oluşur. 

Yukarıdaki toplamda görüldüğü üzere geometrik serinin ilk terimi “a” dır. Geometrik seride art arda gelen iki terim arasında sabit bir oran (r) bulunur. Bu orana ortak çarpan da denir. Ortak çarpan r’nin mutlak değeri 1’den küçük ise (|r|<1) o geometrik serinin toplamı sonlu bir sayıya eşittir.

Bizim sonsuz toplamımıza dönecek olursak; sorumuzun cevabı olan geometrik serinin ilk terimi 24/100, ortak çarpanı ise 56/100’dür. Ortak çarpanın değeri 1’den daha küçük olduğu için geometrik serimiz aslında sonlu bir sayıya eşittir. Peki bu sayıyı nasıl bulabiliriz?

Sorumuzun cevabı olan sayıyı bulmak için öncelikle genel formdaki geometrik seriyi inceleyelim ve |r|<1 için sonlu toplamı bulalım. Daha sonra bulduğumuz formülü örneğimizin cevabı için kullanalım.

Öncelikle geometrik serimizin kısmi toplamını yazalım ve bu toplamı S ile gösterelim.

S=a+ar+ar²+ar³+...+arⁿ

Eşitliğin her iki tarafını ortak çarpan “r” ile çarptığımızda

rS=ar+ar²+ar³+ar⁴+...+arⁿ⁺¹ 

eşitliğini elde ederiz. 

Yukarıdaki iki eşitliğin farkı ise

S-rS=a-arⁿ⁺¹ 

şeklinde yazılabilir. Yani

S(1-r)=a(1-rⁿ⁺¹) 

’dir.

Bu durumda kısmi toplam

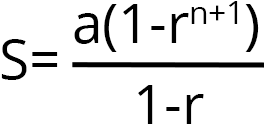  ’ye eşit olur.

Sonsuz toplamın eşiti içinse kısmi toplamın n sonsuza giderken limit değerine bakılır. |r|<1 olduğu için  

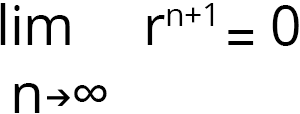’dır.

Bu durumda sonsuz toplamın limiti yani kısmi toplamın limiti 

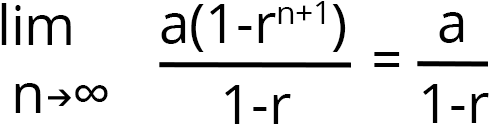 olur.

Bulduğumuz genel formülü örneğimize uyguladığımızda sonsuz toplamın eşiti 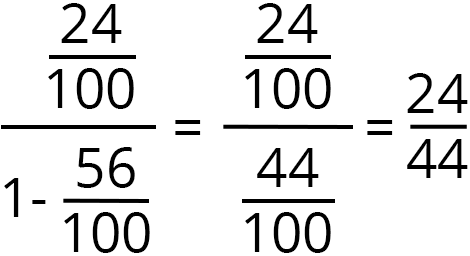olur.

Sonuç olarak, iki arkadaşın oynadığı oyunu 2. kişinin kazanma olasılığı 0,545 veya %54,5 olarak hesaplanır.