Palindrom Sayılar
Binbir Gece Masalları’ndaki “1001” sayısında olduğu gibi, soldan sağa veya sağdan sola yazıldığında aynı olan başka sayılar aklınıza geliyor mu? Peki, palindrom sayı olarak isimlendirilen bu sayıların ilginç özelliklerini öğrenmek ister misiniz?

Sunny/Corbis/Getty Images Plus
Palindrom, hem sağ taraftan hem de sol taraftan okunduğunda aynı olan kelime veya kelime gruplarıdır. Örneğin mum, ada, yapay, kazak, küçük, neden, niçin gibi kelimelerle “ey edip adanada pide ye” veya ‘’zamkı çok o çıkmaz’’ cümleleri birer palindrom örneğidir. Ayrıca Mozart’ın Spiegelkanon bestesi de nota dizilişi bakımından palindrom özelliktedir.
Bu durum sadece kelimelerde veya bestelerde değil sayılarda da karşımıza çıkabilir. Soldan sağa veya sağdan sola doğru yazıldığında aynı olan sayılara ise palindrom sayılar denir. Örneğin Binbir Gece Masalları’ndaki “1001” sayısı bir palindrom sayıdır.

BrianAJackson/iStock.com
Palindrom sayılar, palindrom kelimelere göre daha karmaşıktır. Örneğin hem asal hem palindrom sayılara “asal palindrom sayılar”, hem üçgensel hem palindrom sayılara “üçgensel palindrom sayılar”, hem tam kare hem de palindrom sayılara ise “karesel palindrom sayılar” denir.
Palindrom sayıların tanımını göz önüne alırsak bir basamaklı tüm sayma sayılarının birer palindrom sayı olduğunu söyleyebiliriz. Aynı şekilde 11, 22, 33, 44, … gibi 9 adet iki basamaklı palindrom sayı vardır. İlk on rakamı içeren en küçük asal palindrom sayı ise 1.023.456.987.896.543.201’dir.
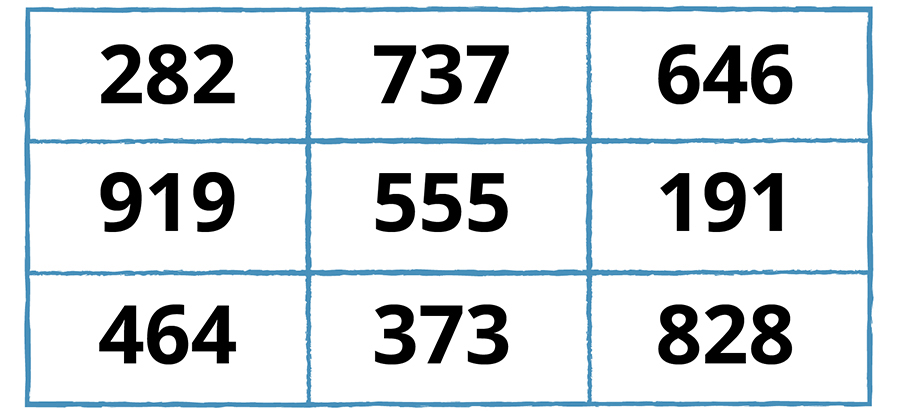
Palindrom sayılar, sihirli kareler gibi, matematiğin estetik yönü ağır basan konularındandır. Örneğin aşağıdaki sihirli kare, palindrom sayılarla üretilmiş sihirli karelerden biridir. Karenin tüm satır ve sütunları ile köşegenlerde bulunan sayıların toplamı 1.665’e eşittir.
Palindrom sayılar astronomide de karşımıza çıkar. Örneğin Merkür’ün, Güneş’in etrafında dolanma süresi 88 gündür. Bu sayı da palindrom bir sayıdır.
Bir basamaklı sayma sayılarının birer palindrom sayı olduğunu ve iki basamaklı 9 adet palindrom sayı olduğunu daha önce belirtmiştik. Üç basamaklı palindrom sayıların formatı ise “aba” şeklindedir. Buradaki “a” için 9 farklı sayıdan (1, 2, 3, … , 9) biri, “b” içinse 10 farklı rakamdan (0, 1, 2, … , 9) biri seçilmelidir. Bu durumda üç basamaklı 90 farklı palindrom sayı bulunur. Yani belirli bir basamakta bulunan palindromların sayısı permütasyon ile hesaplanabilir. Aşağıdaki tabloda belirli basamaklarda kaçar adet palindrom sayı olduğu sayı formatlarıyla birlikte görülebilir.
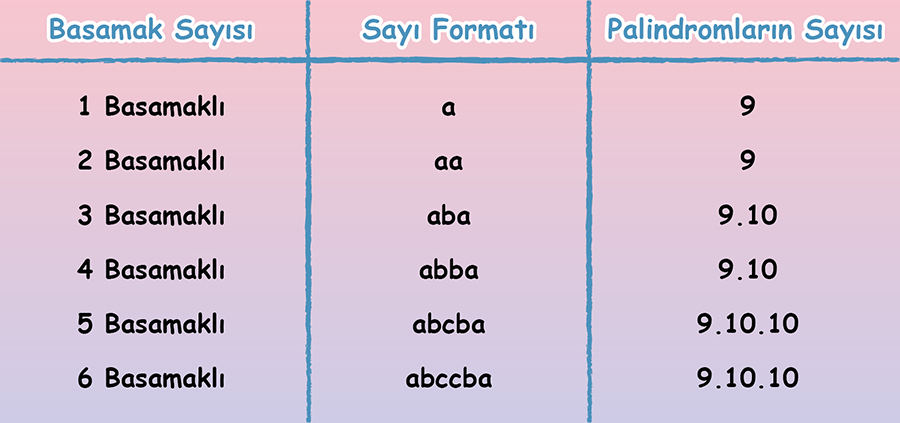
Bir n sayısı için 1 ile 10n arasında (1 dâhil olmak üzere) kaç adet palindrom sayı bulunduğunu W(P) ile gösterilen formülle hesaplayabiliriz:
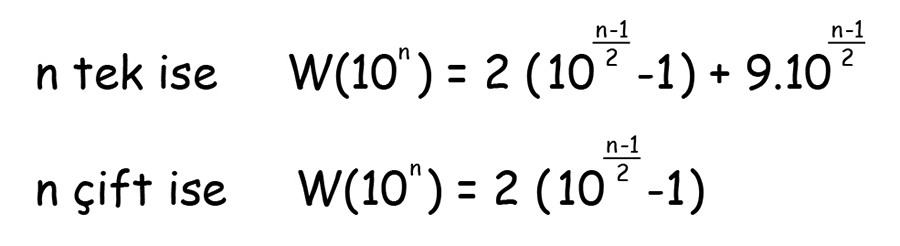
Örneğin n=3 sayısı için W(103)=2(10-1)+9(10)=108’dir. Yani 1 ile 1000 arasında (1 dâhil olmak üzere) 108 adet palindrom sayı vardır.
Herhangi bir sayıdan palindrom sayı elde edilebiliriz. Bunun için seçtiğimiz sayıya tersini eklememiz ve bu işlemi palindrom sayı elde edene kadar yinelememiz gerekir. Örneğin 56 sayısını ele alalım. 56 sayısına bu sayının tersi olan 65 sayısını eklediğimizde, ilk adımda palindrom bir sayı olan 121’e (56+65=121) ulaşırız. 57 sayısını seçtiğimizde palindrom bir sayıya iki adımda ulaşırız (57+75=132, 132+231=363). 59 sayısını seçtiğimizde ise palindrom bir sayıya üç adımda ulaşırız (59+95=154, 154+451=605, 605+506=1111).
Palindrom bir sayı elde etmeye çalışırken 196 sayısına dikkat etmeliyiz. Çünkü bu sayıya yukarıdaki işlem 400 milyon kez uygulansa dâhi palindrom bir sayıya ulaşılamaz. 196 sayısına bu sayının tersini eklediğimizde 196+691=887’yi elde ederiz. Bu durumda doğal olarak 691 sayısının da bizi palindrom bir sayıya ulaştırıp ulaştırmayacağı henüz bilinmiyor. 295, 394, 493, 592 gibi sayıları da seçmemeliyiz. Çünkü bu sayıların hepsi birinci adımda bizi 887’ye ulaştırıyor.
Çift basamaklı palindromların tümü 11 ile tam bölünebilir. Örneğin 4 basamaklı bir palindrom sayı “abba” formatındadır. Bu “abba” sayısı ise 11’in katı olarak aşağıdaki gibi yazılabilir.

Diğer çift basamaklı palindrom sayıların da 11 ile tam bölündüğünü siz gösterebilirsiniz. Ayrıca palindrom sayıların diğer özelliklerini araştırarak kendiniz öğrenebilirsiniz.
Kaynaklar:
- Clifford, A. P., A Passion for Mathematics: Numbers, Puzzles, Madness, Religion, and the Quest for Reality, John Wiley & Sons, New Jersey, 2005.
- http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/IntegerReps/palindromes.html
- https://math.ou.edu/~jalbert/courses/byrnes_glascock.pdf
- https://e-dergi.tubitak.gov.tr/edergi/yazi.pdf?dergiKodu=4&cilt=31&sayi=368&sayfa=46&yaziid=10781
- https://www.jstor.org/stable/pdf/24925878.pdf?refreqid=excelsior%3A2065c7f6df83e9520a913167850fbad7