Aristo’nun Tekerlek Paradoksu
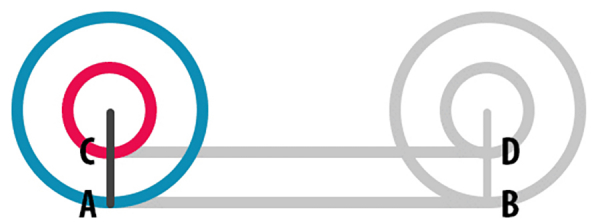
Farklı yarıçaplara sahip, ortak merkezli iki dairesel tekerlek düşünelim. Bu tekerlekleri kaydırmadan bir tam tur döndürdüğümüzde, tekerleklerin aldığı mesafelerin birbirine eşit olması imkânsız görünüyor değil mi? Peki, bu kafa karıştırıcı durum nasıl açıklanabilir?
Çizim: Erhan Balıkçı
Antik Yunanca bir eser olan Mechanica’da geçen ve Aristo’nun tekerlek paradoksu olarak bilinen durumu anlamak için ortak merkezli dairesel iki tekerlek düşünelim. Dıştaki büyük tekerleğin yarıçapı, içteki küçük tekerleğin yarıçapının iki katı olsun. Şimdi dıştaki tekerlek çevresi etrafında kaydırılmadan bir tam tur döndürüldüğünde, iç içe geçmiş bu tekerleklerin ne kadar mesafe aldığını inceleyelim.
Çizim: Erhan Balıkçı
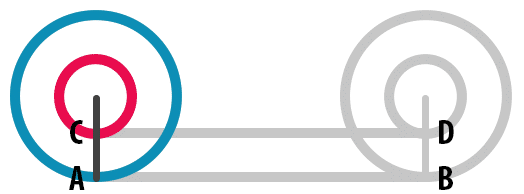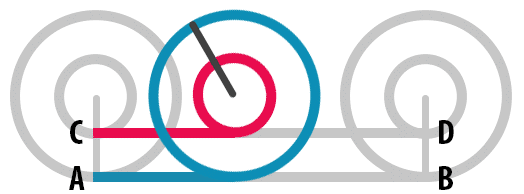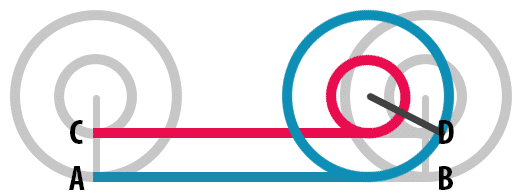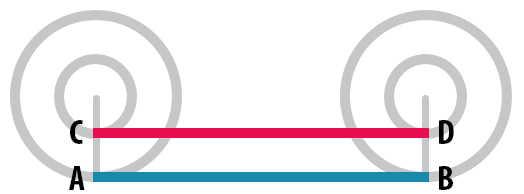
Yukarıdaki animasyonda görüldüğü gibi, ortak merkezli iki tekerlek bir tam tur döndürüldüğünde dıştaki büyük tekerlek A ile B noktaları arasındaki uzunluk kadar yol alırken içteki küçük tekerlek C ve D noktaları arasındaki uzunluk kadar yol kateder. Yani tekerleklerin aldığı mesafeler birbirine eşit olur.
Herhangi bir çemberin çevresi etrafında kaymadan bir tam tur döndüğünde katedebileceği mesafenin, çemberin çevre uzunluğuna eşit olduğunu biliyoruz. Örneğin r birim yarıçaplı bir tekerleğin, çevresi etrafında kaymadan bir tam tur döndüğünde alabileceği mesafe 2πr’dir.

Peki o hâlde yukarıdaki ortak merkezli, farklı yarıçaplara (dolayısıyla farklı çevre uzunluklarına) sahip iki tekerleğin katettiği mesafeler nasıl aynı oluyor?
Gelin şimdi hep birlikte bu tekerleklerin nasıl eşit yol aldığını öğrenelim.
Yüzyıllar boyunca bilim insanları, Aristo’nun tekerlek paradoksunun arkasında yatan matematiği anlamaya çalıştılar. Bunlardan biri de ünlü gök bilimci Galileo’ydu. Galileo öncelikle ortak merkezli, altıgen şeklindeki tekerleklerin hareketini inceledi. Örneğin aşağıdaki gibi iç içe geçmiş ABCDEF ve KLMNOP altıgenlerini ele alalım ve dıştaki altıgenin çevre uzunluğunun, içteki altıgenin çevre uzunluğunun iki katı olduğunu varsayalım.
Çizim: Erhan Balıkçı
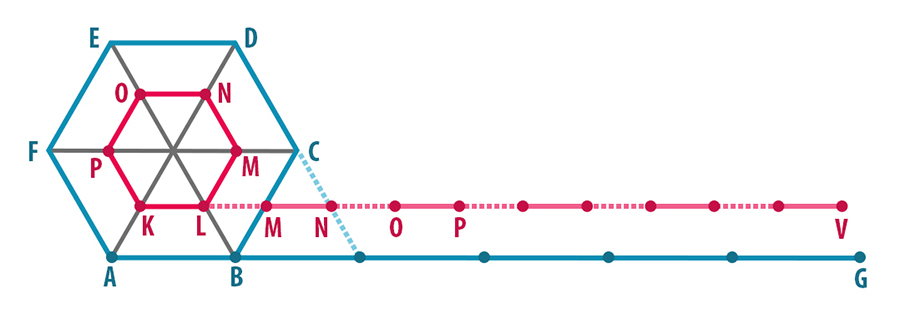
Başlangıçta dıştaki tekerlek, AB kenarı zeminde olacak şekilde hareketsizdir. Dıştaki tekerlek sağa doğru döndürüldüğünde sırasıyla BC, CD, DE, EF ve FA kenarları zemine değecek şekilde altı eş parçaya bölünmüş AG doğru parçası üzerinde ilerler. Büyük tekerleğin çevre uzunluğu AG doğru parçasının uzunluğuna eşittir.
Dıştaki tekerlekle birlikte hareket eden içteki küçük tekerlek ise başlangıçta KL kenarı üzerinde hareketsizdir. Daha sonra sırasıyla LM, MN, NO, OP, PK kenarlarının üzerine gelerek KV doğru parçası üzerinde ilerler. Fakat küçük tekerleğin ilerleyişi büyük tekerleğin ilerleyişinden biraz farklıdır. Çünkü küçük tekerlek, sağa doğru ilk hareketinde KV doğru parçasının LM bölümünü atlar ve MN bölümünün üzerine gelir. İkinci adımda ise küçük tekerleğin MN kenarı, KV doğru parçasının NO bölümünü atlayarak OP bölümünün üzerine gelir. Altıgen şeklindeki tekerlekler bir tam tur döndürüldüğünde, ilk ve son konumda tekerleklerin merkezleri arasındaki mesafe birbirine eşit olur. Fakat büyük tekerlek tüm yolu katederken, küçük tekerlek yolun bazı bölümlerini atlayarak yol alır.
Eğer tekerlekler daha fazla kenara sahip düzgün çokgenlerden oluşsaydı, yine içteki tekerlek yolu atlayarak tamamlardı. Fakat bu durumda atlanan bölümler daha sık aralıklı ve daha kısa olurdu.
Galileo, çok sayıda kenara sahip düzgün bir çokgenin sezgisel olarak çembere benzediğini ve bu tekerlekler döndüğünde küçük tekerleğin yolu yine atlayarak tamamlayacağını düşündü. Fakat Galileo’nun bu düşüncesi aslında doğru değildi. Çünkü içteki dairesel küçük tekerlek CD doğrusundan hiç ayrılmadan yol alır. Başka bir deyişle, küçük tekerleğin dönme hareketi büyük tekerleğinki gibi süreklidir ve büyük tekerleğin AB doğrusuna temas eden noktası sürekli değiştiği gibi küçük tekerleğin de CD doğrusuna temas eden noktası sürekli değişir. Bu durumda, çemberlerin (Çember sabit bir noktaya yani merkeze eşit uzaklıktaki sonsuz noktalar kümesidir.) üzerindeki noktalar ile doğru parçalarının üzerinde bulunan sonsuz noktalarla bire bir eşleşir.
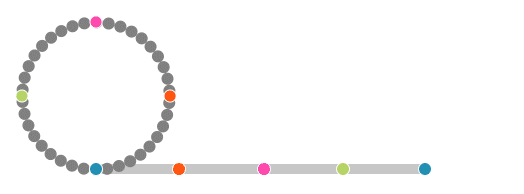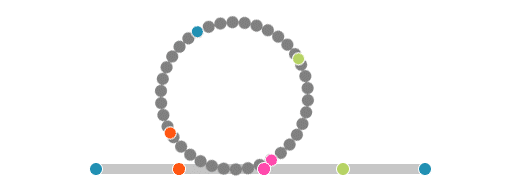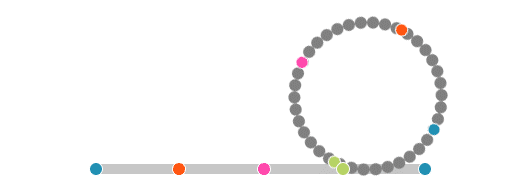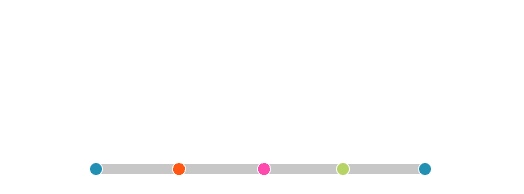
Çizim: Erhan Balıkçı
Önceleri küçük çember ile CD doğru parçasının noktalarının bire bir eşleşmesinin, çember ile yolun aynı uzunlukta olmasını gerektirdiği zannediliyordu. Fakat Aristo’nun tekerlek paradoksunun çözümüyle bu bilginin yanlış olduğu anlaşıldı. Yani küçük çember ile CD doğrusu üzerindeki noktaların bire bir eşleşmesi, ikisinin aynı uzunlukta olduğu anlamına gelmez. Örneğin aşağıdaki doğru parçalarını inceleyelim. Doğru parçaları farklı uzunluklarda olmasına rağmen, üzerlerindeki noktalar bire bir eşleşir.
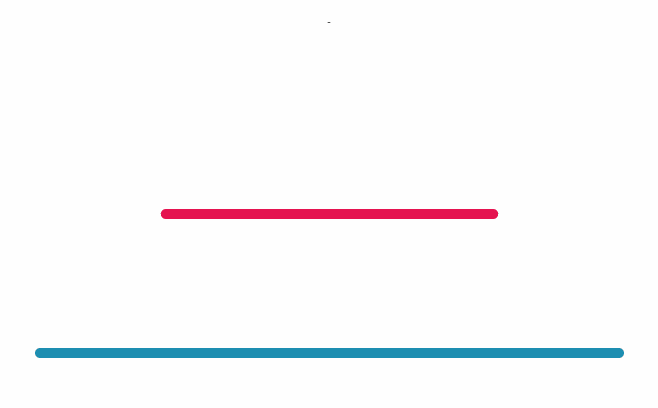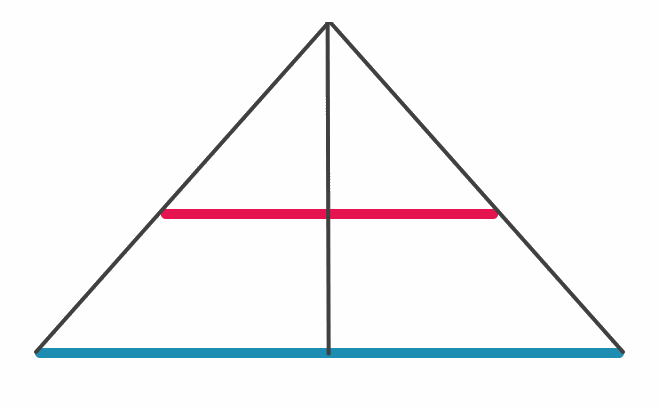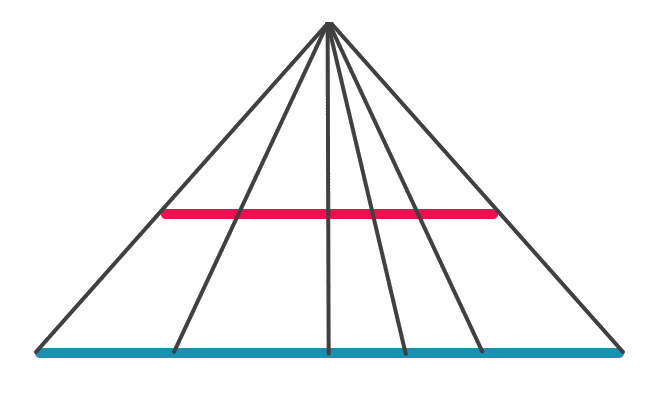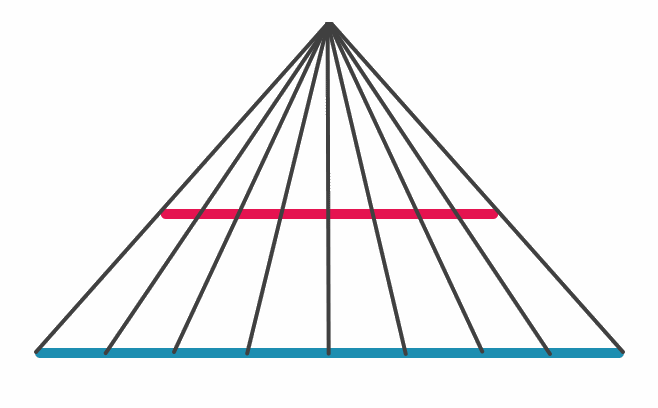
Çizim: Erhan Balıkçı
Aynı şekilde dairesel tekerleklerin uzunlukları da birbirinden farklıdır fakat noktalar bire bir eşleşir. Herhangi iki eğri üzerindeki noktaların bire bir eşleşmesinin eğrilerin aynı uzunlukta olmasını gerektirmediğini kanıtlayarak, Aristo’nun tekerlek paradoksunu çözen ilk kişi ise Alman matematikçi George Cantor’dur. Paradoksun çözüm anahtarı ise süreklilik ve sonsuz kümeler kavramlarıdır.
Kaynaklar: