Çemberin Çevre Uzunluğu Neden 2πr’ye Eşittir?

Herhangi O merkezli, r yarıçaplı bir çemberin çevre uzunluğunun 2πr’ye eşit olduğunu ispatlamak için ilk olarak çemberin içerisine şekildeki gibi bir köşesi çemberin merkezinde bulunan dört eş üçgen çizelim. Bu dört üçgenin taban uzunlukları toplamı, görselden de anlaşılacağı üzere, çemberin çevre uzunluğundan bir hayli küçüktür. Çemberin içerisindeki dört üçgen aslında bir eşkenar dörtgen oluşturur.

Peki, çemberin içerisine daha fazla sayıda üçgen yerleştirdiğimizde ne olur?

Şimdi de çember içerisine tepe noktaları çemberin merkezinde bulunan sekiz eş üçgen yerleştirelim. Yani çemberin içerisine düzgün sekizgen çizelim. Bu durumda, düzgün sekizgenin kenar uzunlukları toplamı çemberin çevre uzunluğuna biraz daha yaklaşır. Ancak bu iki uzunluk hâlâ birbirine eşit değildir. Görselden de anlaşılacağı üzere düzgün sekizgenin kenar uzunlukları toplamı, çemberin çevre uzunluğundan daha küçüktür. Yine de ilk duruma göre çokgenin çevre uzunluğu, çemberin çevre uzunluğuna biraz daha yaklaşmıştır.

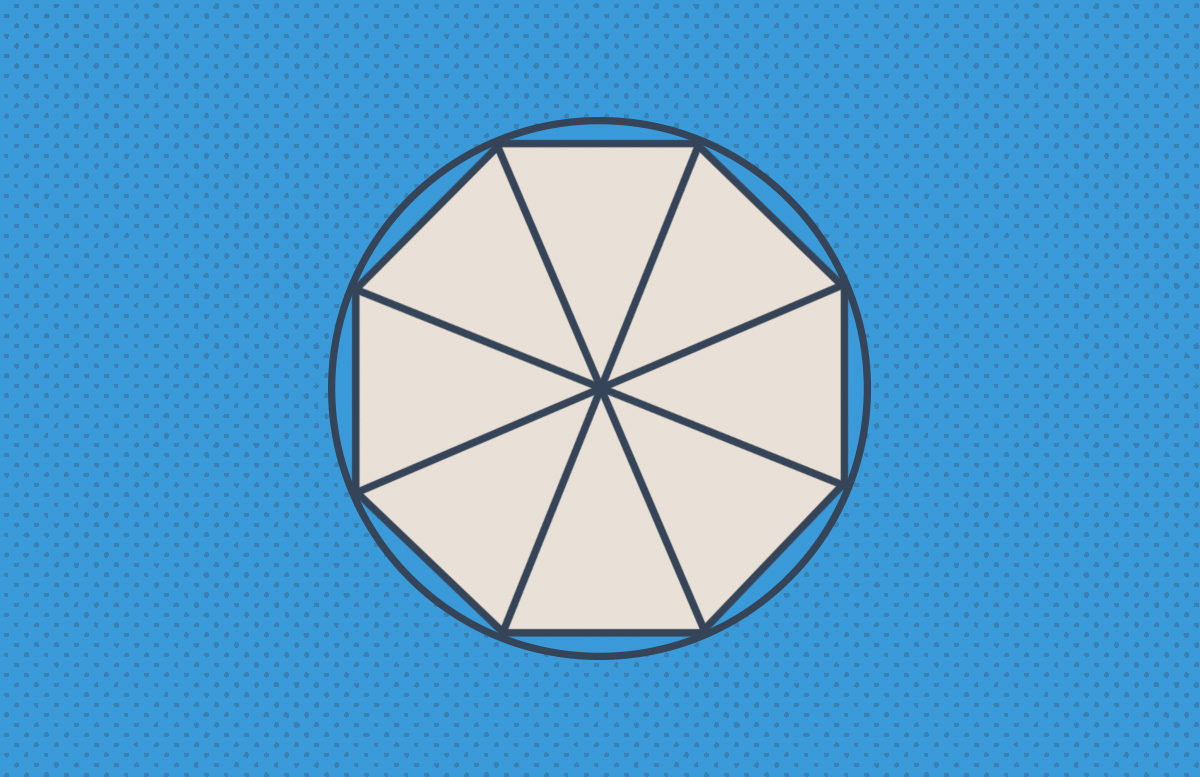
Çemberin içerisindeki düzgün çokgenin kenar sayısını artırdığımızda, çokgenin kenar uzunlukları toplamı ile çemberin çevre uzunluğu birbirine yaklaşır. Ancak çemberin içerisine ne kadar fazla kenarlı bir çokgen yerleştirilirse yerleştirilsin, kenar sayısı aslında sonlu olacağı için bu iki sayı değer olarak birbirine yaklaşsa bile hiçbir zaman eşit olmaz.

Peki, sizce çemberin içerisine sonsuz kenarlı bir düzgün çokgen yerleştirilebilseydi ne olurdu? 

İşte bu durumda çokgenin kenar uzunlukları toplamı çemberin çevre uzunluğuna yakınsardı. Nasıl mı?

Çemberin içerisine n kenarlı düzgün bir çokgen yerleştirdiğimizi düşünelim. 

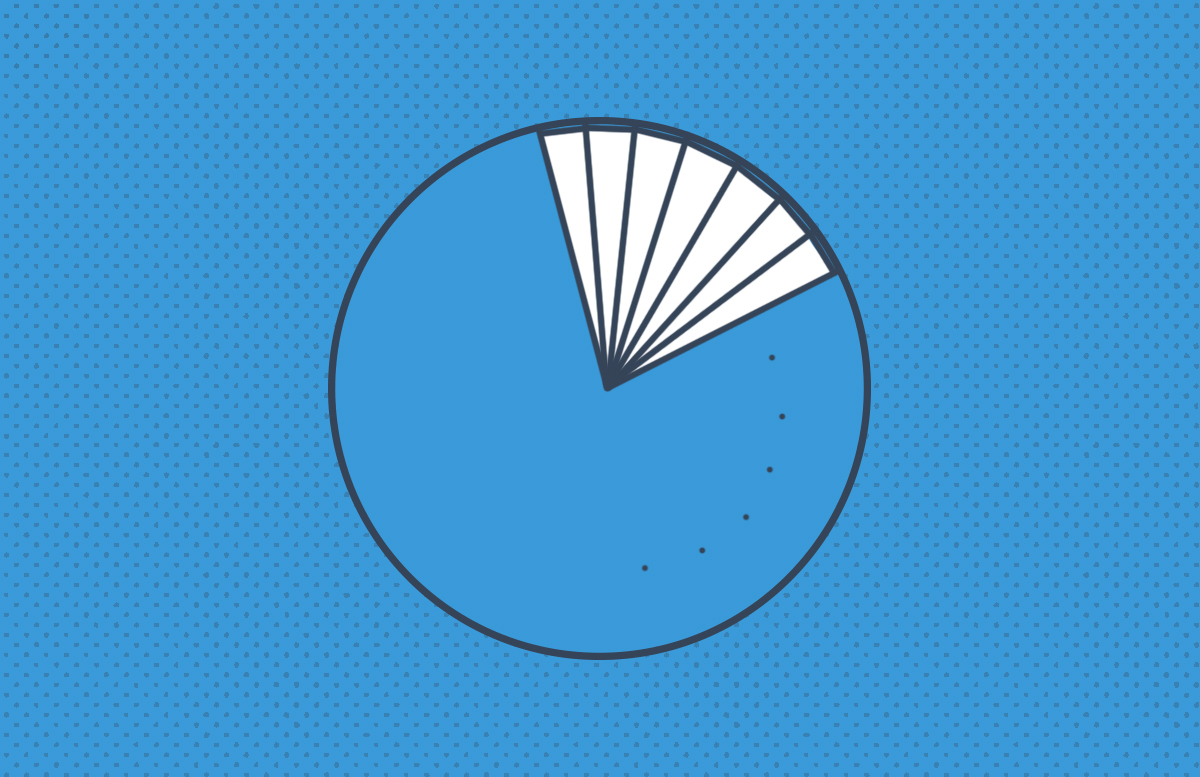
Bu n kenarlı düzgün çokgen aslında tepe noktaları çemberin merkezinde bulunan n adet birbirine eş üçgenden oluşur. Bu üçgenlerin tepe açılarının ölçüsü birbirine eşit ve θ=2π/n derecedir. Aynı şekilde tüm üçgenlerin taban uzunlukları ve yan kenar uzunlukları birbirine eş olur. Üçgenlerin taban uzunlukları “L”, kenar uzunlukları ise “r” birim olsun.  Bu durumda ortaya çıkan ikizkenar üçgenlerden biri aşağıda gösterilmiştir.

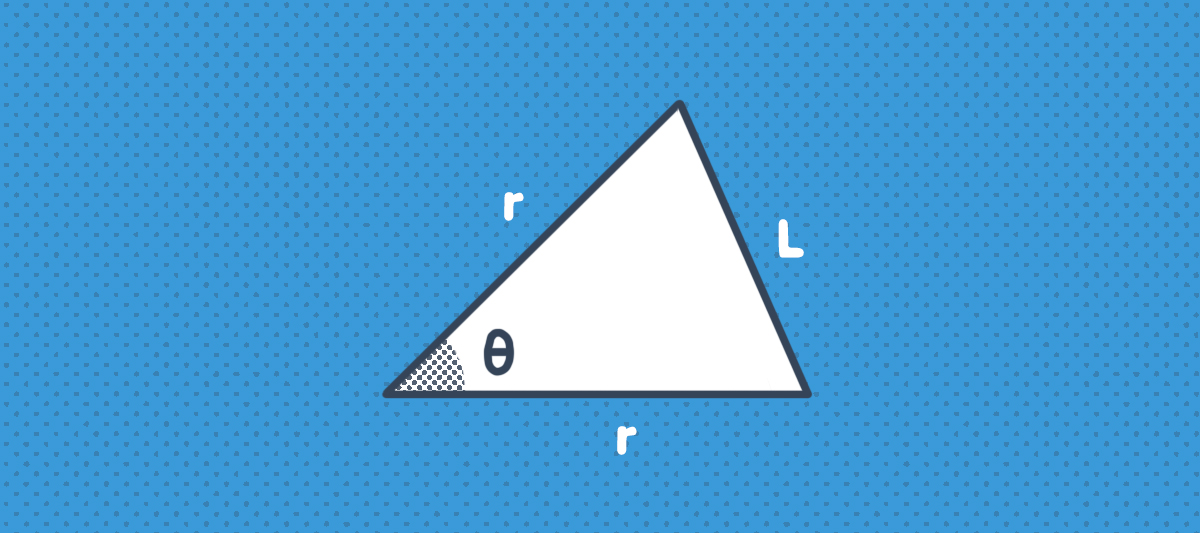
İkizkenar üçgende tabana çizilen dik çizgi, tabanı ve üçgenin açısını iki eş parçaya böler. Bu durumda aşağıdaki eşitliği elde ederiz:

 sin(θ/2)=(L/2)/r.

θ=2π/n olduğu için eşitliğimiz aslında sin(π/n)= L/(2r) şeklindedir.

n kenarlı çokgenin kenar uzunlukları toplamına P dersek P=nL olur veya bir başka deyişle P=nL=n(2r)sin(π/n)’dir.

Çokgenin kenar sayısını ifaden eden n’yi çok büyük bir sayı olarak düşündüğümüzde, çokgenin çevre uzunluğu çemberin çevre uzunluğuna yakınsar. Bu durumun matematiksel ifadesi

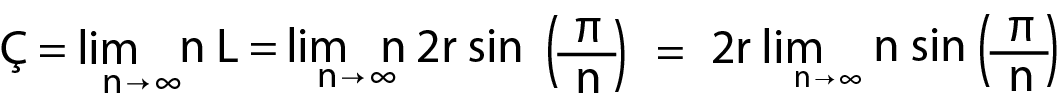
şeklindedir.

Yukarıdaki üçüncü eşitlikte 2r değeri, n sonsuza giderken bakılan limit değerinin sabit sayısıdır. Yani bu sayı limit değerinin katsayısıdır.

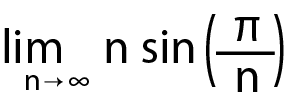  ifadesinin değerinin ise π’ye yakınsadığı L’Hospital kuralı ile gösterilebilir.

Sonuç olarak çemberin çevre uzunluğu, Ç=2πr eşitliği elde edilmiş olur.

Matematikte limit kavramının ne olduğunu öğrenmek için “Matematikte Limit Nedir?” başlıklı yazımıza buradan ulaşabilirsiniz.