Matematikte Limit Nedir?

Extreme-Photographer/iStock.com

Belirli bir mesafenin yarısı gidildikten sonra geriye kalan mesafenin sürekli olarak yarısı katedildiğinde bu işlem sonsuza kadar sürer ve otobüs durağına hiçbir zaman varamayız. Çünkü otobüs durağına ulaşmak için kalan yolun uzunluğu ne kadar küçük olursa olsun yarısı hesaplanabilir. Yani kalan mesafe hiçbir zaman 0’a eşit olmaz. Ancak 0’a çok yaklaşır. İşte matematikteki limit kavramıyla da bir fonksiyondaki x değerleri belirli bir sayıya yaklaşırken fonksiyon grafiğinin nasıl davranacağı gözlemlenir.

Matematikte limit kavramından bahsedildiğinde aslında verilen bir fonksiyonun limiti anlaşılır. Örneğin her bir sayıyı, kendisinin çarpımsal tersine götüren bir fonksiyon düşünelim. Bu fonksiyon matematiksel olarak f(x) = 1/x şeklinde ifade edilir ve 2 sayısını 1/2’ye, 5 sayısını da 1/5’e götürür. 

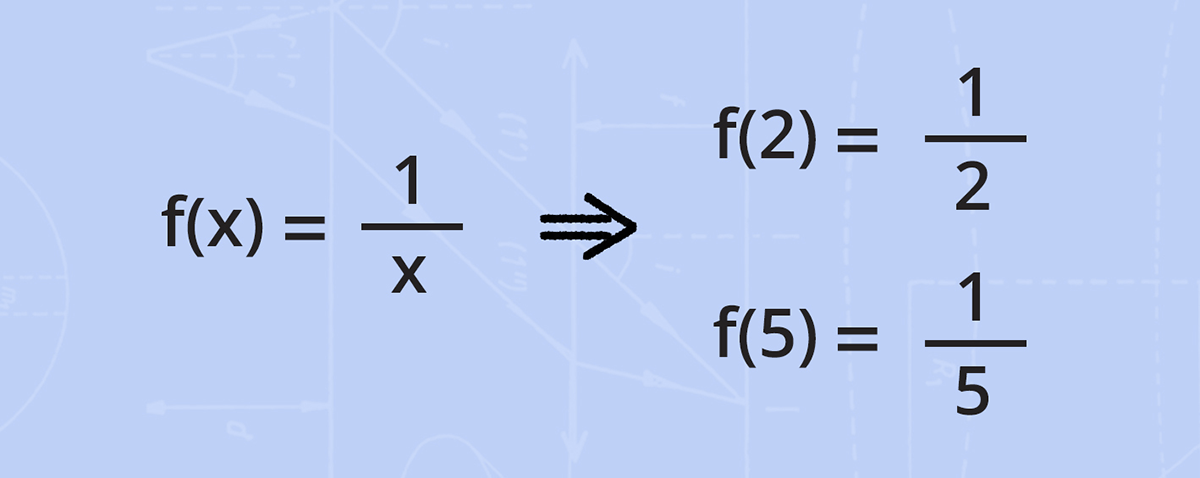
f(x)=1/x fonksiyonu x=0’da tanımsızdır. Ancak, bu fonksiyon x=0’da tanımlı olmasa da, x değeri 0’a yaklaştığında fonksiyon grafiğinin nasıl davranacağını, 0’a çok yakın değerleri alarak görebiliriz.

Bunun için öncelikle x değerini 1’e eşit alalım (x=1). Bu değer 0’ın sağında ve 0’dan oldukça uzaktadır. x değeri 1’e eşitken, fonksiyonumuzun değeri 1’dir yani f(1)=1.

Şimdi 0’a biraz daha yaklaşalım ve x değerini 1/2 olarak seçelim. Bu durumda fonksiyonun değeri 2 olur. Bu şekilde sayılarımızı 0’ın sağından ve 0’a giderek yaklaştırdığımızda f(x) fonksiyonunun değerlerinin giderek büyüdüğünü gözlemleyebiliriz.

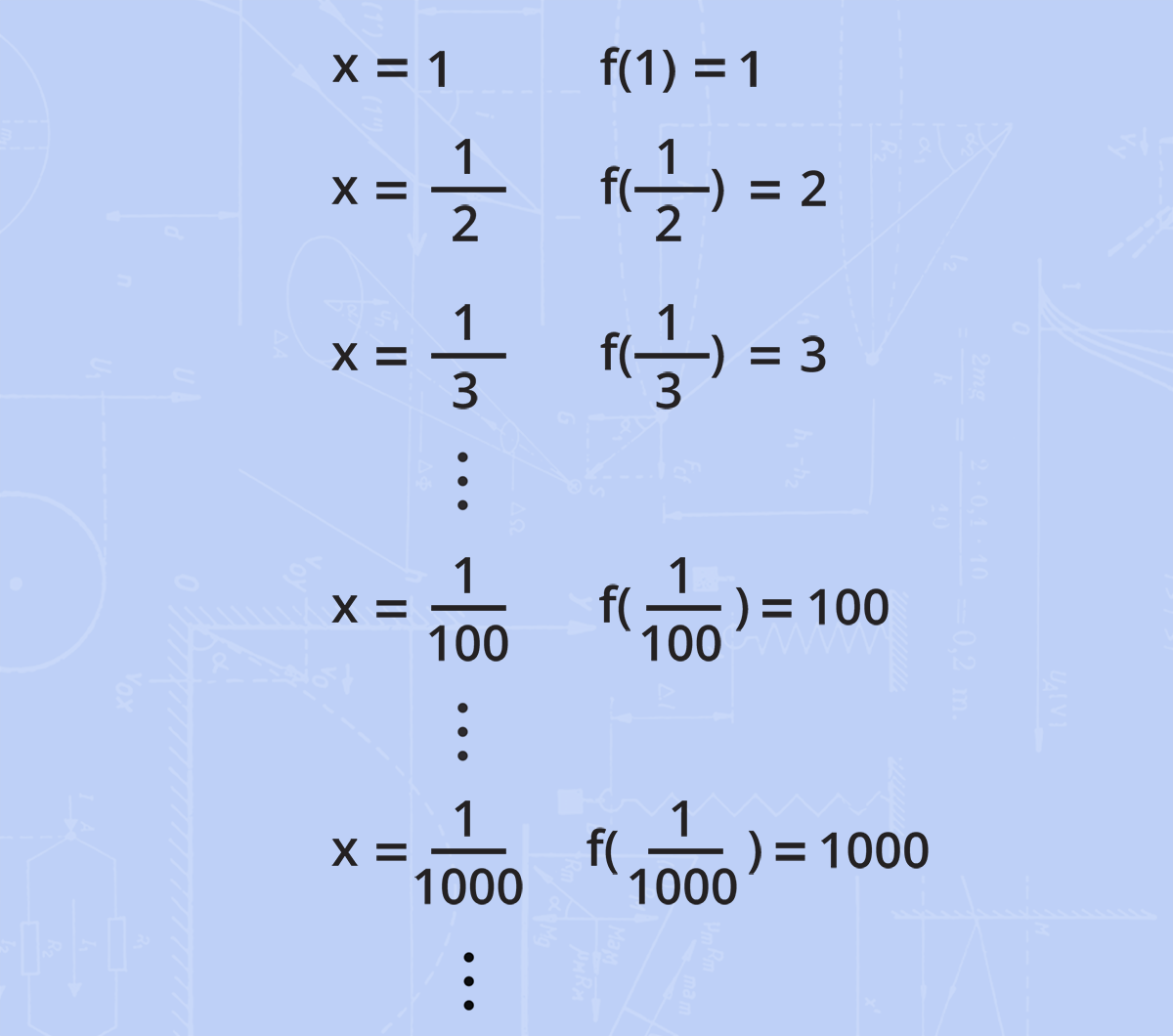
Fonksiyonun değerlerinin istenildiği kadar büyük yapılması için x değerlerinin 0’ın sağında yani pozitif ve 0’a çok yakın seçilebileceği görülür. Bir başka deyişle, x değerleri 0’a sağdan yaklaşırken f(x) fonksiyonunun değerleri sonsuza gider. Bu durumu limit kavramı ile ifade edecek olursak, x’in aldığı değer 0’a sağdan yaklaşırken f(x) fonksiyonunun aldığı değer sonsuza yaklaşır yani f(x) fonksiyonunun limiti sonsuzdur. Matematiksel olarak da

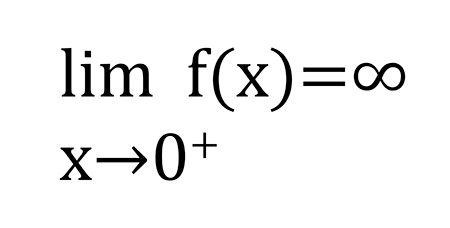
şeklinde yazabiliriz. Sonsuz (∞) ise reel bir sayı olmadığından x değeri 0’a sağdan yaklaşırken aslında fonksiyonun ulaştığı bir limit değeri yoktur.

Şimdi başka bir durumu daha inceleyelim ve aynı fonksiyonun x değerleri yeterince büyük seçildiğinde limitin nereye yaklaşacağını gözlemleyelim. x değerleri 1, 5, 100 ve 1000 alındığında fonksiyonun değerleri sırasıyla 1, 1/5, 1/100 ve 1/1000 olur. Yani x değerleri büyüdükçe fonksiyonun değerleri giderek küçülür ve x değeri çok büyük alındığında f(x) fonksiyonunun grafiği 0’a yaklaşır. Bu durumun matematiksel olarak ifadesi ise

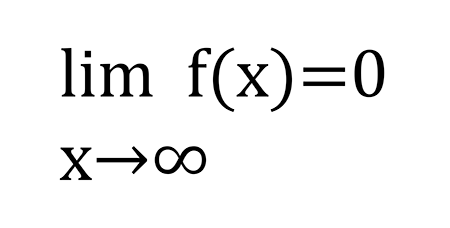
şeklindedir.

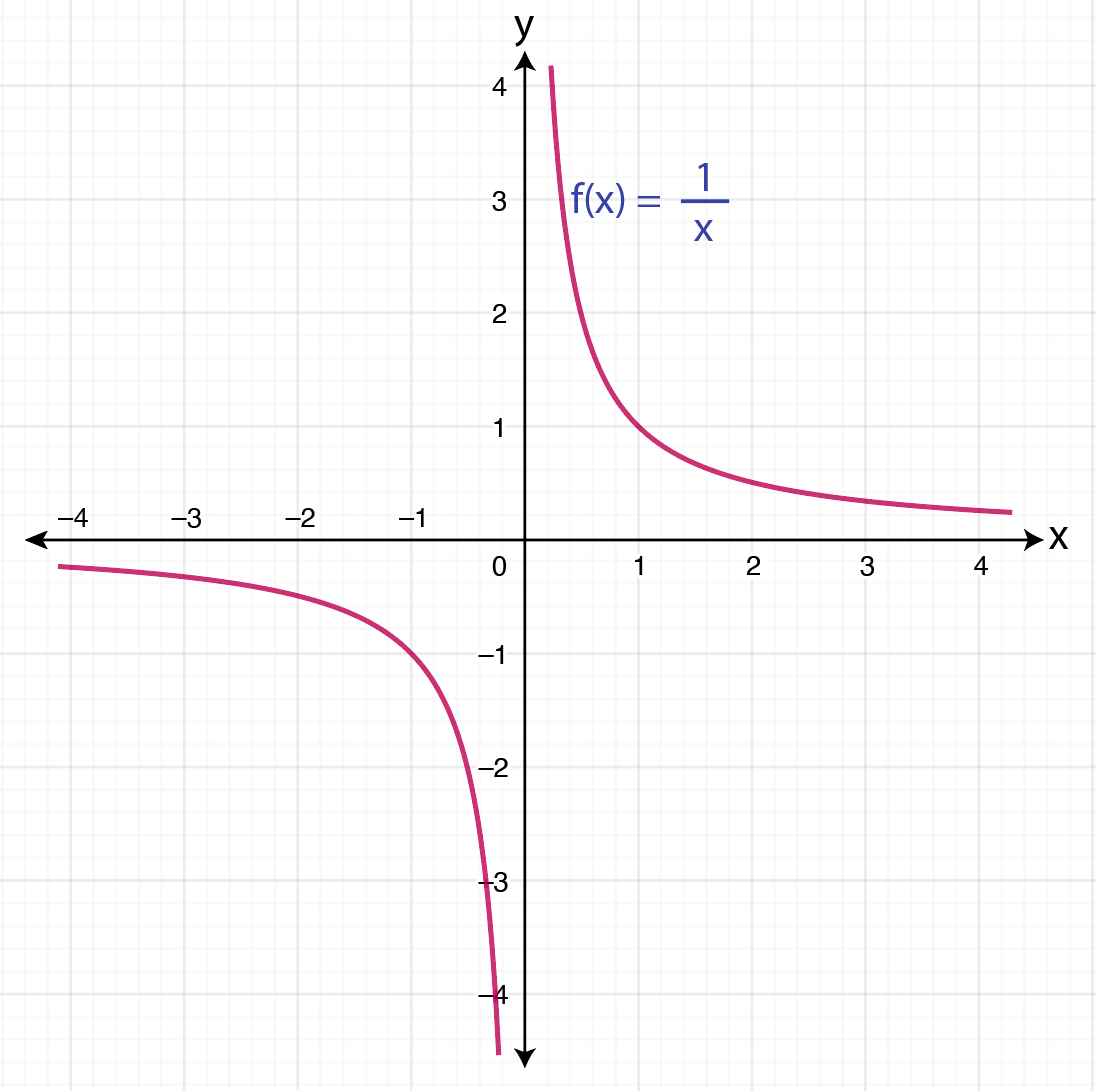
Yukarıda hesapladığımız limitler, x değerleri belirli bir sabit değere yaklaşırken f(x)=1/x fonksiyonunun bir değere yakınsayıp yakınsamadığını gösterir. Bu davranışları f(x)=1/x fonksiyonunun grafiğini inceleyerek de görebiliriz.

İlk örneğimizde x değeri 0’a sağdan yaklaştığında fonksiyonun limitini sonsuz bulduk. 

Peki sizce x değerleri 0’a soldan yaklaştığında fonksiyonun limiti ne olur? x değerleri yeterince büyük ve negatif alındığında fonksiyonun değeri nereye yaklaşır? 

Yukarıdaki sorulara doğru cevap verdiğiniz takdirde f fonksiyonunun 0’ın solundaki ve eksi sonsuzdaki (- ∞) limitinin ne olduğunu keşfetmiş olursunuz. (İpucu: Grafiğe bakarak bunu kendiniz de çıkarabilirsiniz.).

Ayrıca limit, matematik derslerinin temeli olan türev ve integral kavramlarının tanımlanmasında bizlere yardımcı olan bir terimdir. Türev, bir niceliğin başka bir niceliğe göre değişimidir. Örneğin yolun zamana bağlı değişimi olan hız veya hızın zamana bağlı değişimi olan ivme türev kavramı ile tanımlanır. Türev uygulamalarına farklı alanlardan da örnekler verilebilir: ekonomi ve ticaret alanlarında kullanılan maksimum kâr ve minimum maliyet hesapları gibi. Genellikle türevin tersi olarak bilinen integral kavramı ise belirli bir aralıktaki toplam değişimi belirtir. Ayrıca integral pozitif eğriler için eğrinin altında kalan alanın hesaplamasında kullanılır.