Trigonometri: Sinüs, Kosinüs ve Tanjant Nedir?
Sinüs, kosinüs ve tanjant, trigonometrideki üç temel fonksiyondur. Bu üç temel trigonometrik fonksiyon, bir açısı 90° olan bir dik üçgende kenarlar ve açılar arasındaki oranların incelenmesini sağlar.

wakila / iStock
Sinüs, kosinüs ve tanjant, trigonometrideki üç temel fonksiyondur. Bu üç temel trigonometrik fonksiyon, bir açısı 90° olan bir dik üçgende kenarlar ve açılar arasındaki oranların incelenmesini sağlar.
Analitik düzlemde merkezi orijin ve yarıçapı 1 birim olan çembere birim çember denir. Trigonometrik fonksiyonlar birim çemberde tanımlı fonksiyonlardır.
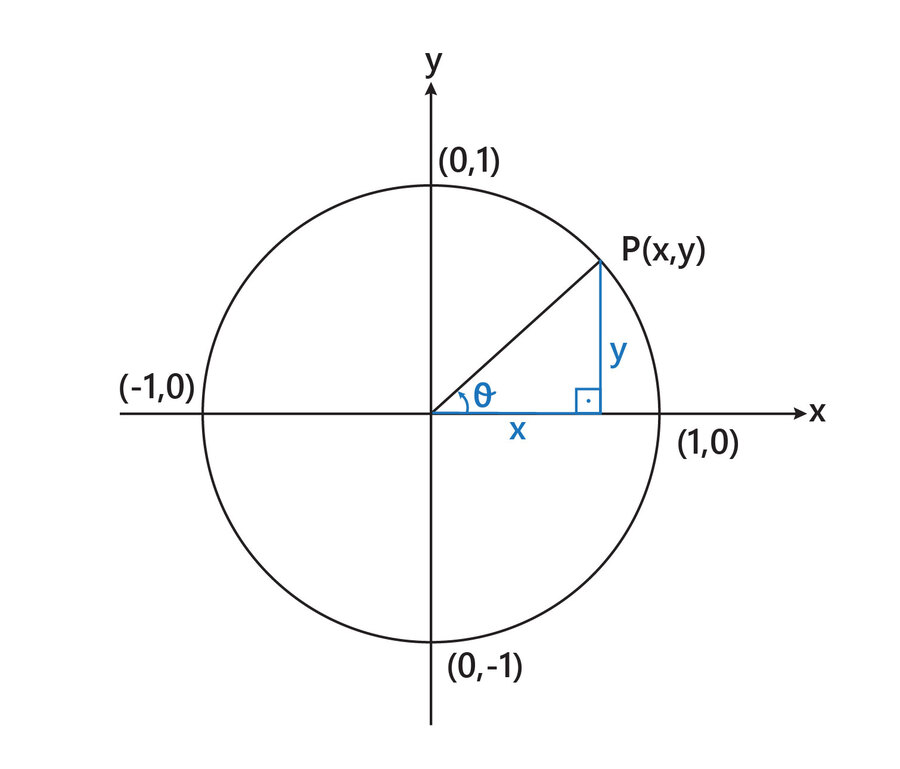
Birim çember üzerindeki bir P noktasının apsis ve ordinat değerleri sırasıyla x ve y ise sinθ ve cosθ değerleri şöyle bulunur: sinθ değeri θ açısının karşı kenar uzunluğunun hipotenüs uzunluğuna oranıdır yani sinθ = y 1 'dir. Cosθ değeri ise θ açısının komşu kenar uzunluğunun hipotenüs uzunluğuna oranıdır yani cosθ = x 1 'dir.
Buradan y = sinθ ve x = cosθ eşitlikleri elde edilir.
Ayrıca P noktası, birim çember üzerinde olduğundan birim çember denklemini sağlar yani x2 + y2 = 1 eşitliği sağlanır. Bu eşitlikte x ve y yerine sinüs ve kosinüs değerleri yazıldığında ise sin2 θ + cos2 θ = 1 eşitliği elde edilir. Bu eşitlik Pisagor özdeşliği olarak bilinir. Bu özdeşlik sayesinde bir açının sinüs (kosinüs) değeri biliniyorsa kosinüs (sinüs) değeri bulunabilir. Hatta bir açının sadece sinüs değeri biliniyorsa kosinüs değeri ve tanjant değeri de hesaplanabilir.
Yukarıda birim çemberde yer alan dik üçgenin θ açısının tanjant değeri tanθ ile gösterilir.
Tanθ = sinθ cosθ = y/1 x/1 = y x 'dir. Yani tanjant değeri, θ açısının karşı kenar uzunluğunun komşu kenar uzunluğuna oranı ile ifade edilir.
Bir dik üçgendeki farklı açıların oluşturduğu sinüs, kosinüs değerleri aşağıdaki gibi sıralanır.
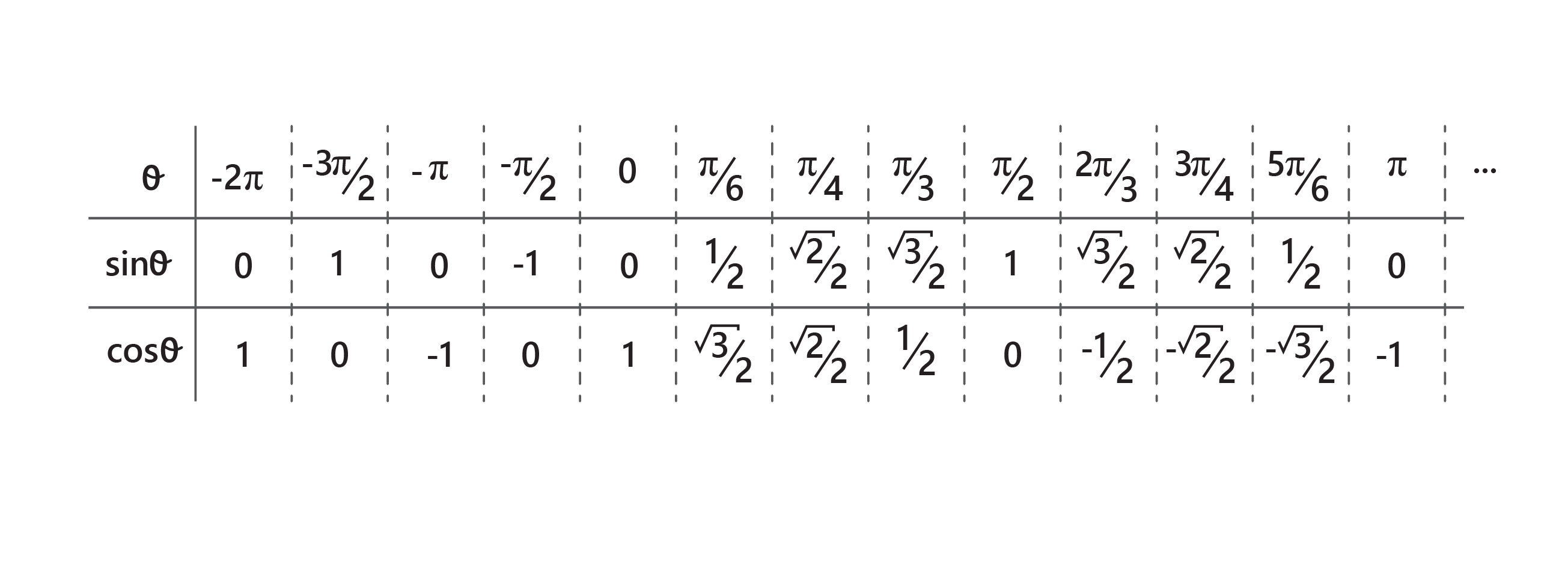
Sinüs ve kosinüs fonksiyonlarının aldığı değerlerin belirli aralıklarla kendini tekrarladığı yani periyodik birer fonksiyon olduğu, tablodan görülebilir. Sinüs ve kosinüs fonksiyonlarının periyotları 2π’dir. Tanım kümesi tüm gerçek sayılardan oluşan bu fonksiyonların görüntü kümesi ise -1 ile 1 arasında salınır.
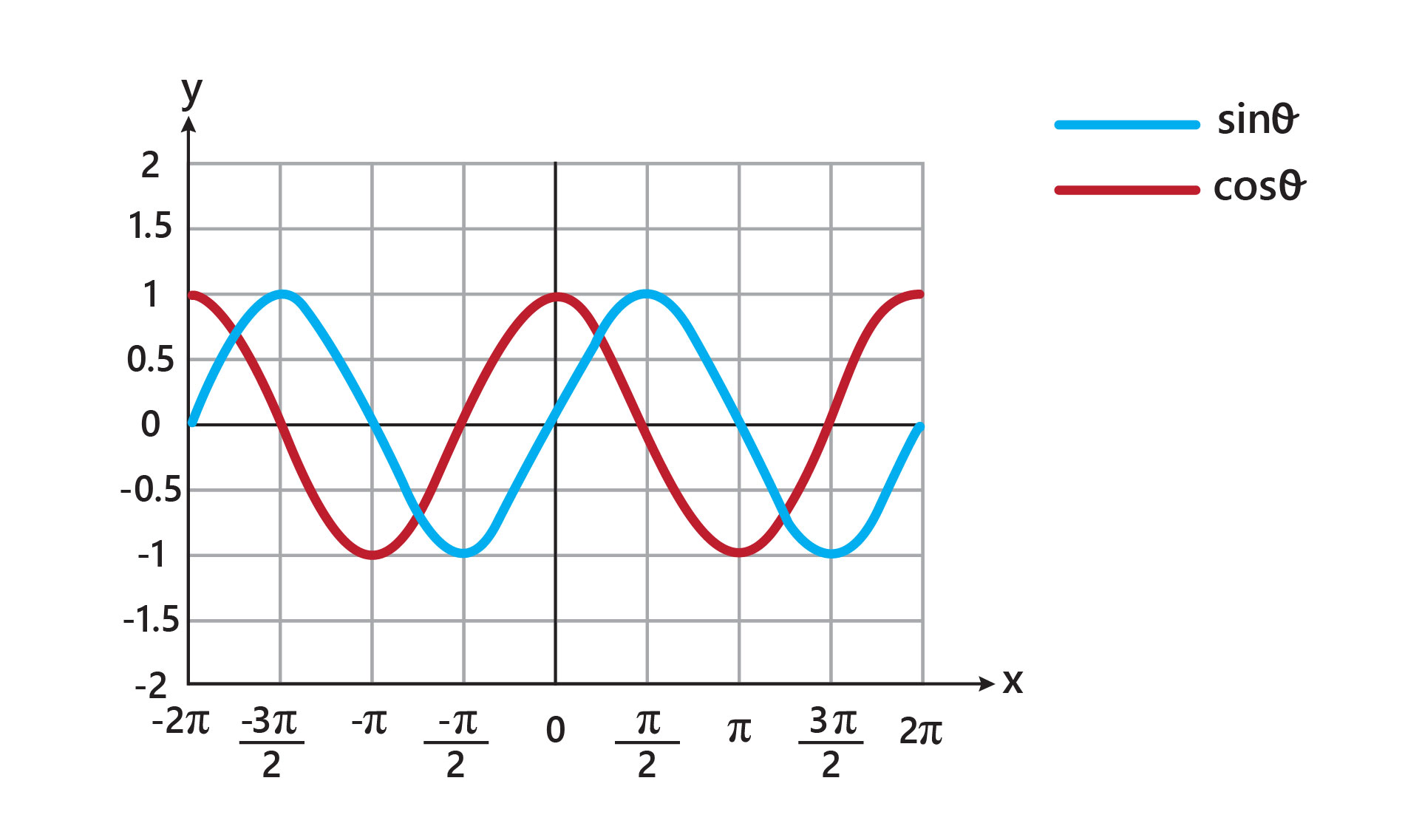
Tanjant fonksiyonu da yine periyodik bir fonksiyondur. Ancak tanjant fonksiyonu (tanθ = sinθ/ cosθ) cosθ fonksiyonunun 0 olduğu noktalarda tanımlanamaz. Bu nedenle tanjant fonksiyonunun grafiği çizilirken dikkatli olunmalı.
Peki Sinüs ve Kosinüs Fonksiyonları Günlük Yaşamda Nerelerde Kullanılır?
Bu fonksiyonlar ve trigonometri, birçok uygulamada karşımıza çıkar. Bina ve köprü tasarımlarının analizleri buna örnektir. Tasarlanan bir yapının açı ve uzunluk analizi yapılarak dayanıklılığı değerlendirilir. Elektrik devrelerinde kullanılan sinüs ve kosinüs fonksiyonları yönü ve şiddeti zamana göre değişen alternatif akımların analizinde kullanılır. Bu fonksiyonlar ayrıca tıp ve astronomi alanlarında da kullanılır. Tıbbi görüntüleme tekniklerinden MR taramaları gibi çeşitli tıbbi cihazlarda insan vücudu tarafından üretilen elektromanyetik sinyaller, gezegen hareketleri, okyanus gelgitleri ve uydu hareketleri de sinüs ve kosinüs fonksiyonlarıyla temsil edilir.
Kaynaklar: