Meşhur Eğri Kardiyoit
Birçoğumuz buğulu bir cama kalp şekli çizmekten hoşlanırız. Peki bu eğrinin arkasındaki matematiği keşfetmek ister misiniz?
Chaloemphon Wanitcharoentham/EyeEm/Getty Images
Kalp şekline benzeyen bir eğri olan kardiyoit, r yarıçaplı sabit bir çember etrafında kaymadan yuvarlanan, yine r yarıçaplı çemberin çevresi üzerindeki herhangi bir noktanın izlediği yol olarak tanımlanabilir.
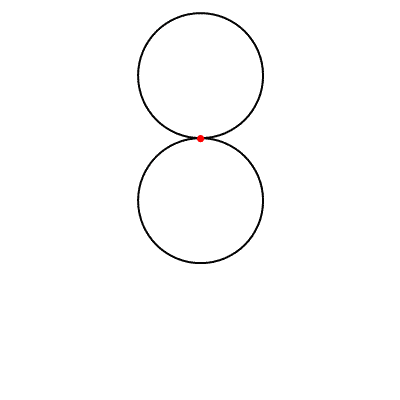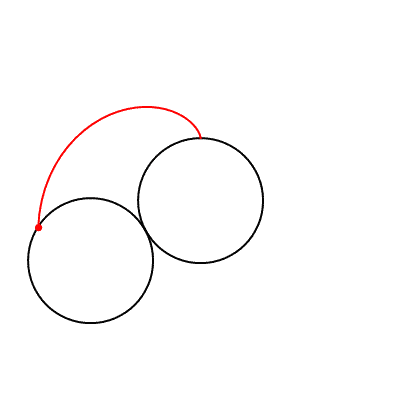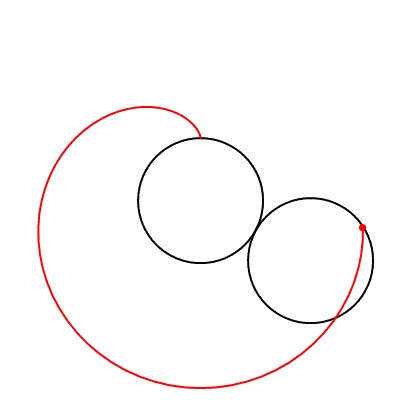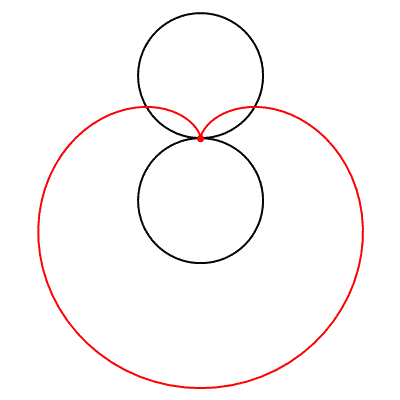
Bu eğriye kardiyoit ismini, 1741 yılında eğriyi inceleyen İtalyan matematikçi Johann Castillon vermiş. Kardiyoit kelimesi Yunancada “kalp” anlamına gelen kardia ve “şekil” anlamına gelen eidos kelimelerinden türetilmiş.
Peki kardiyoit eğrisini nasıl çizebiliriz?
Bu eğri farklı yöntemlerle çizilebilir.
Birinci Yöntem:
İlk olarak çapı 17 cm olan bir çember çizelim. Daha sonra bu çember üzerinde eşit aralıklarla 52 nokta belirleyelim ve bu noktaları 0’dan 51’e kadar numaralandıralım. Ardından n ile numaralandırılmış her noktayı 2n ile numaralandırılmış nokta ile düz çizgiler kullanarak birleştirelim. 26 numaralı noktadan itibaren noktaların sayı değerlerinin iki katı çember üzerinde bulunmaz. Bu nedenle n=26’dan itibaren, noktaları 2n değerinden 52 çıkararak elde ettiğimiz noktalarla birleştirelim.
İkinci Yöntem:
Kardiyoit eğrisi matematiksel olarak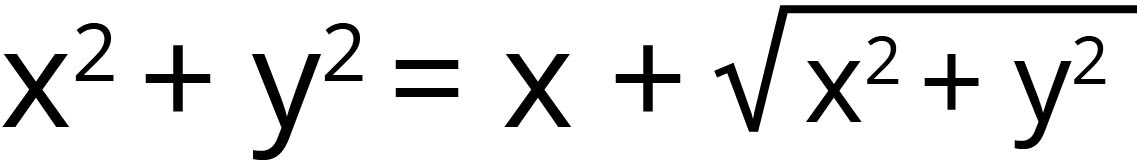 
eşitliğiyle ifade edilir. Dolayısıyla kardiyoit eğrisi kutupsal koordinat sisteminde de kolaylıkla çizilebilir. Eğrinin çiziminden önce koordinat sistemiyle bildiklerimizi hatırlayalım:
Düzlemdeki bir noktanın yeri koordinat sistemiyle belirlenir. Örneğin orijinden a birim sağda ve b birim yukarıda bulunan bir P noktası koordinat sisteminde aşağıdaki gibi gösterilirken (solda), aynı nokta kutupsal koordinat sisteminde (r,θ) sıralı ikilisiyle ifade edilir. Bu koordinat sisteminde P noktasının orijinden uzaklığı r ile, yatay eksenle yaptığı açı ise θ ile gösterilir (sağda). Buradan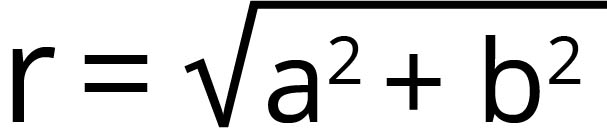 
olduğu kolayca görülür.
Kartezyen koordinat sisteminden kutupsal koordinat sistemine x=rcosθ ve y=rsinθ eşitlikleriyle geçilir. Kartezyen koordinat sisteminde 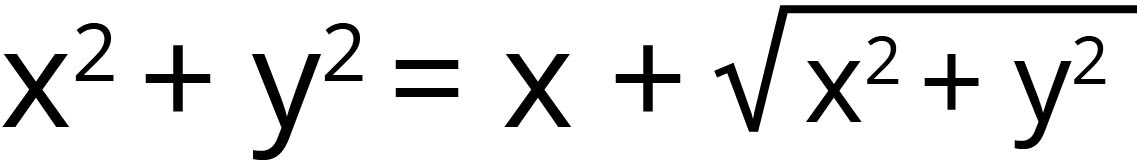eşitliğiyle ifade edilen kardiyoit eğrisinin kutupsal koordinat sistemindeki denklemi r=1+cosθ olur. (x=rcosθ ve y=rsinθ eşitlikleri kullanılarak kolayca gösterilebilir.)
Şimdi de kardiyoit eğrisini kutupsal koordinatlar sisteminde çizelim. Öncelikle θ açısının yatay eksenle yaptığı açı 180º olana kadar inceleyelim. Yani ilk olarak şeklin yarısını çizmeye çalışalım. Bildiğimiz açılar için cosθ’nın değerini ve ardından 1+cosθ uzunluğunu yani r’yi hesaplayalım.
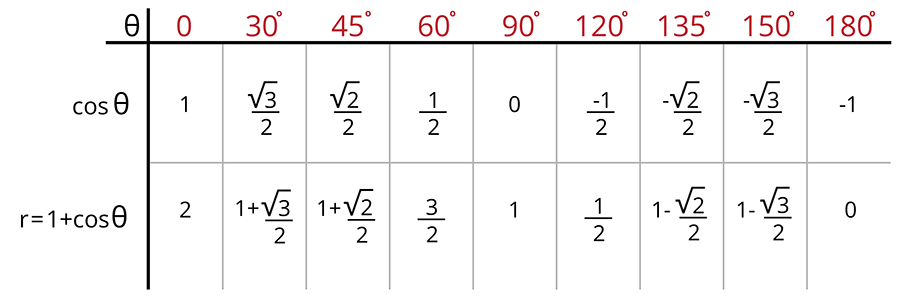
Yatay eksenle yapılan değişik açılarda kardiyoit eğrisinin orijinden uzaklığını hesapladık. Şimdi bu değerler ile eğrinin yarısını çizebiliriz. Örneğin eğrinin yatay eksenle yaptığı açı 30º olduğunda eğri üzerindeki noktanın orijinden uzaklığı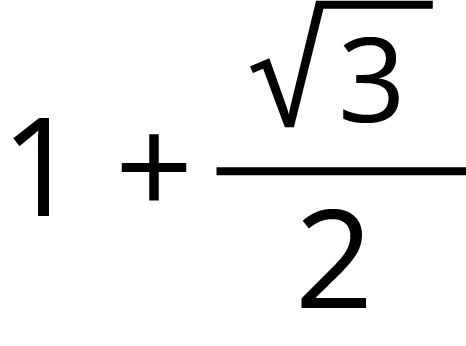 
’dir. Aynı şekilde eğrinin yatay eksenle yaptığı açı 60º olduğunda eğri üzerindeki bu noktanın orijinden uzaklığı 3/2 olur. Bu şekilde kutupsal koordinat sisteminde belirlediğimiz bazı noktaları birleştirerek kardiyoit eğrisinin yarısını aşağıdaki gibi çizebiliriz. Daha fazla açı kullanarak ve o açılardaki noktaların orijinden uzaklığını belirleyerek daha doğru bir grafik elde edilebiliriz.
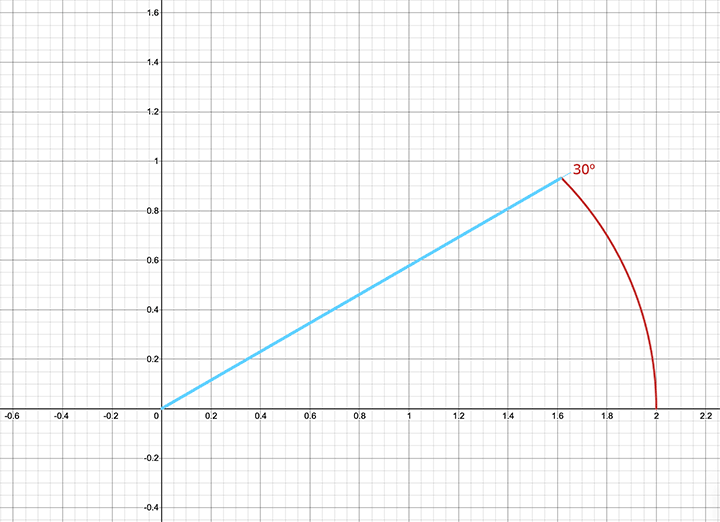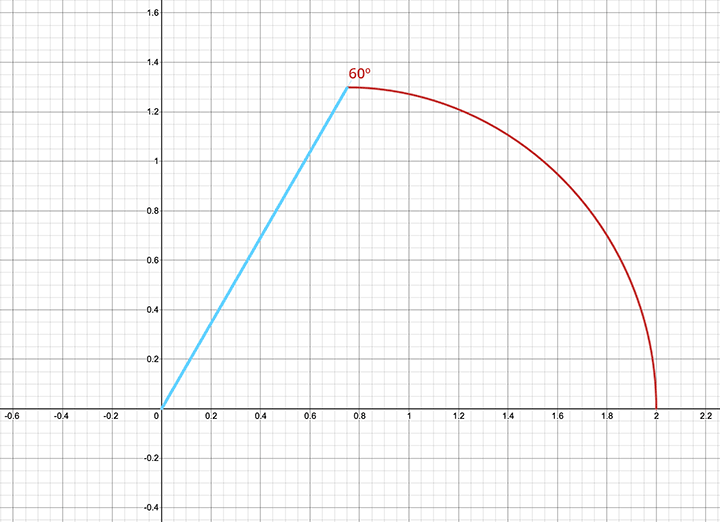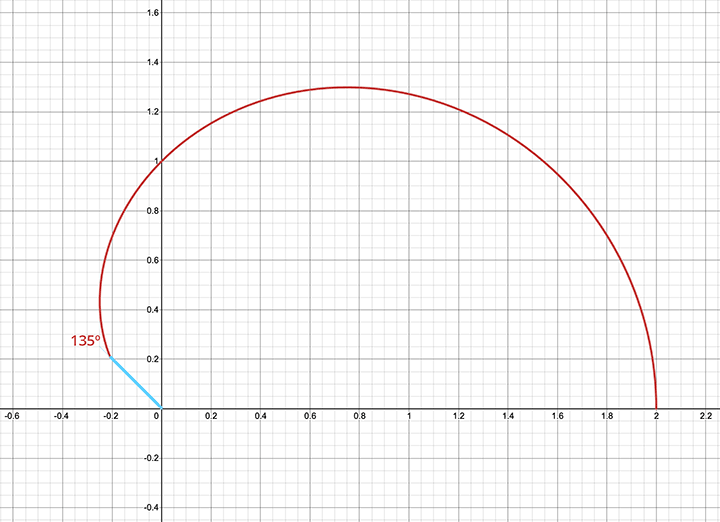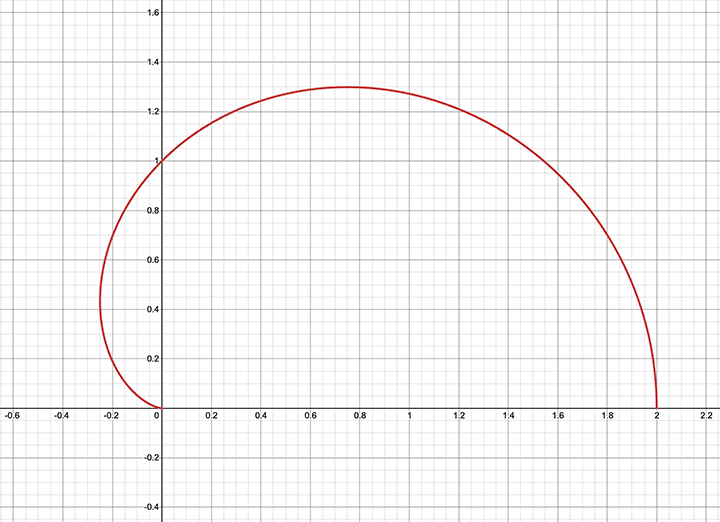
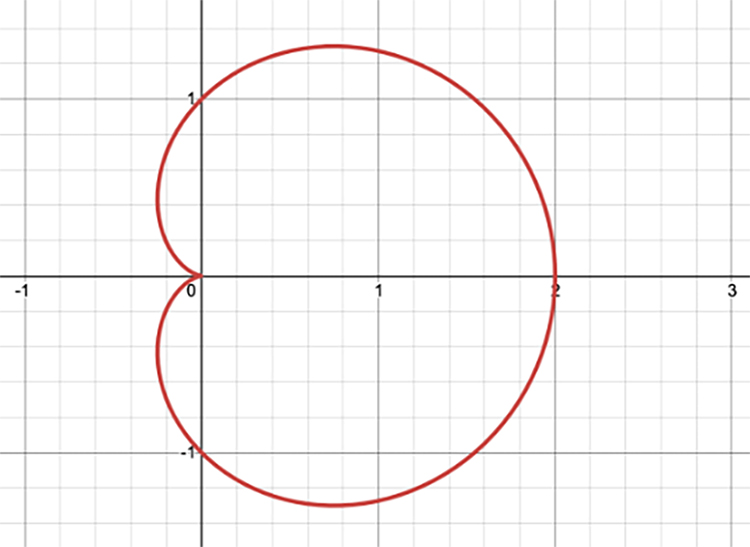
Eğrinin diğer yarısını da 180º ile 360º arasındaki dereceleri kullanarak siz çizebilir veya bu kısımda simetriden yardım alabilirsiniz. Çünkü r=1+cosθ eğrisinin yatay eksene göre simetrik bir eğri olduğunu biliyoruz.
Kaynaklar:
