Skaler ve Vektörel Nicelikler Arasındaki Farklar Nelerdir?

Fizikle ilgili bir kitabı karıştırdığımızda büyük olasılıkla vektörleri içeren formüllerle karşılaşırız. Bu formülleri görmek belki keyfimizi kaçırabilir hatta “Vektörler kullanılmadan bu konu anlatılamaz mı?” diye içimizden geçirdiğimiz durumlar da olabilir. Vektörleri ve vektörel işlemleri anlamak başlangıçta zor olsa da anladıktan sonra değişik uygulama alanlarını keşfetmek eğlencelidir.

Vektör Nedir?

Vektörler bisikletin neden devrilmeden iki teker üzerinde hareket edebildiğini, bir topacın dönüşünü veya uçakların rotalarını sabitlemede kullandığı mekanik jiroskopların nasıl çalıştığını anlamamızda büyük kolaylık sağlar. Vektörler, karmaşık kavramlar gibi görünseler de hız ve kuvvet gibi fizikte çok kullanılan yönlü fiziksel niceliklerle işlemler yapmak için gereklidir. Yön içeren işlemlerde, işlem sonrası yönlerin nasıl değiştiğini takip etmekte büyük kolaylık sağlarlar. Bu özelliklerinden dolayı vektörel nicelikler fiziksel olayları tanımlamak ve anlamak için fiziğin birçok alanında sıklıkla kullanılır.

Skaler Nicelik (Büyüklük) Nedir?

Fizikte kullanılan bazı nicelikler sadece büyüklükleriyle ifade edilebilir. Örneğin bir cismin kütlesini sadece bir sayıyla tam olarak tanımlayabiliriz çünkü kütlenin sadece sayısal bir değeri vardır, yönü yoktur. Sadece büyüklükleriyle ifade edilebilen fiziksel nicelikler skaler nicelikler ya da skaler büyüklük olarak adlandırılır. Kütle, sıcaklık, enerji, zaman, hacim, basınç, ısı, iş skaler büyüklüklerdir.

Skaler niceliklerle bildiğimiz toplama, çıkarma, çarpma ve bölme işlemlerini basitçe yapabiliriz. Skaler niceliklerle işlem yaparken sadece büyüklüklerini yani sayısal değerlerini göz önünde bulundurmak yeterlidir. Örneğin 30 kilogram elmayla 60 kilogram elmayı topladığımızda elimizde toplamda 90 kilogram elma olacağını kolaylıkla hesaplayabiliriz.

Vektörel Nicelik (Büyüklük) Nedir?

Fizikte yaygın olarak kullanılan hız ve kuvvet gibi bazı nicelikler ise skaler niceliklerden farklıdır; bu niceliklerin büyüklüklerinin yanı sıra yönleri de vardır. Bu niceliklerin sadece sayısal değerini bilmek yetmez, “ne tarafa” yönelmiş olduklarını da bilmemiz ve bunu hesaplara dâhil etmemiz gerekir. Bir aracın hızının büyüklüğünün (sürat) yanı sıra ne tarafa (yön) doğru gittiğini bir arada ifade edebilirsek o zaman bu aracın hızını tam olarak tanımlamış oluruz. Hem yönü hem de büyüklüğü olan nicelikler vektörel nicelikler ya da vektörel büyüklükler olarak adlandırılır. Hız, kuvvet, ivme, momentum, elektrik ve manyetik alan vektörel niceliklerdir.

Vektörlerle yapacağımız toplama, çıkarma, çarpma ve bölme gibi matematiksel işlemlerde hem büyüklük hem de yönleri göz önünde bulundurmamız gerekir. Aksi takdirde yanlış sonuçlar hatta bazı durumda anlamsız sonuçlarla karşı karşıya kalabiliriz.

Vektörlerle Matematiksel İşlemler Nasıl Yapılır?

Sadece büyüklüğü olan skaler niceliklerle dört işlemin kolaylıkla yapılabildiğine yukarıda değinmiştik. Peki yön özelliği olan niceliklerle yani vektörlerle matematiksel işlemleri nasıl yaparız? Vektörlerle toplama ve çıkarma yapmak görece kolay olsa da özellikle çarpma ve bölme işlemi alışık olduğumuz çarpma ve bölme işleminden farklıdır çünkü “yönleri” nasıl çarpıp böleceğimizi uygun şekilde tanımlamamız gerekir.

Vektörel Nicelikler Nasıl Toplanır?

Örneğin hızları sırası ile 30 km/h ve 60 km/h olan iki aracın hızlarını toplamaya çalışalım. Hızların toplamı 30 km/h + 60 km/h = 90 km/h midir? Hızların toplamı, eğer iki araç aynı yönde hareket ediyorsa 90 km/h olur. Eğer bu iki araç ters yönlerde hareket ediyorsa sonuç 90 km/h değil 30 km/h olacaktır. Hızlar gelişigüzel yönlerde ise toplam hız 30 km/h ile 90 km/h arasında herhangi bir değerde olabilir. Görüldüğü gibi vektörlerle toplama yaptığımızda yön özelliği sonucu büyük ölçüde farklılaştırabiliyor.

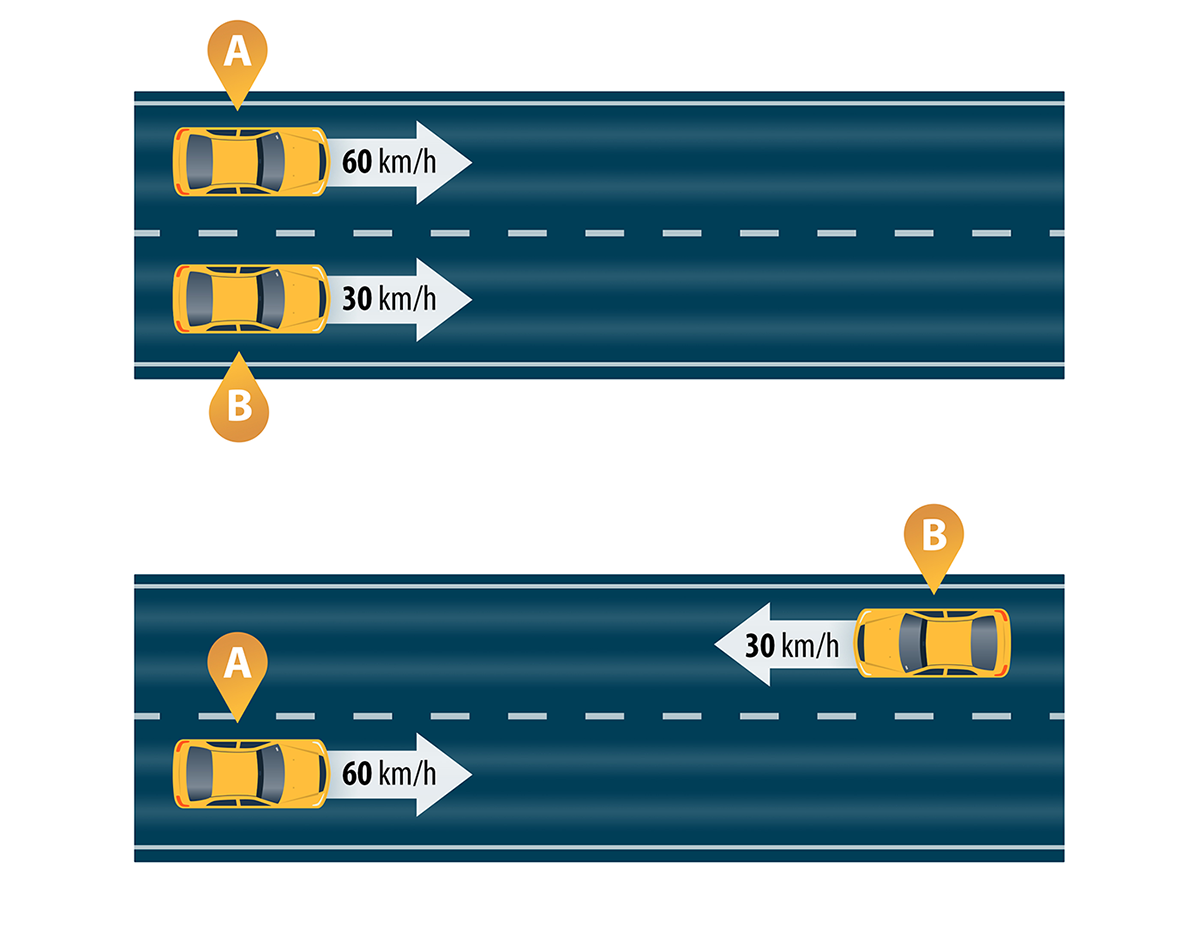
Vektörel Nicelikler Nasıl Bölünür?

İşlemlere yön kavramını dâhil ettiğimiz zaman oluşan en ilginç durumlardan biri iki vektörü birbirine bölme işlemidir. Normal sayılarla kolayca yaptığımız bölme işlemini yönleri olan niceliklerle yaptığımızı düşünelim. Kuzeye doğru 60 km/h hızla giden bir aracın hızını doğuya doğru 30 km/h hızla giden bir aracın hızına nasıl bölebiliriz?

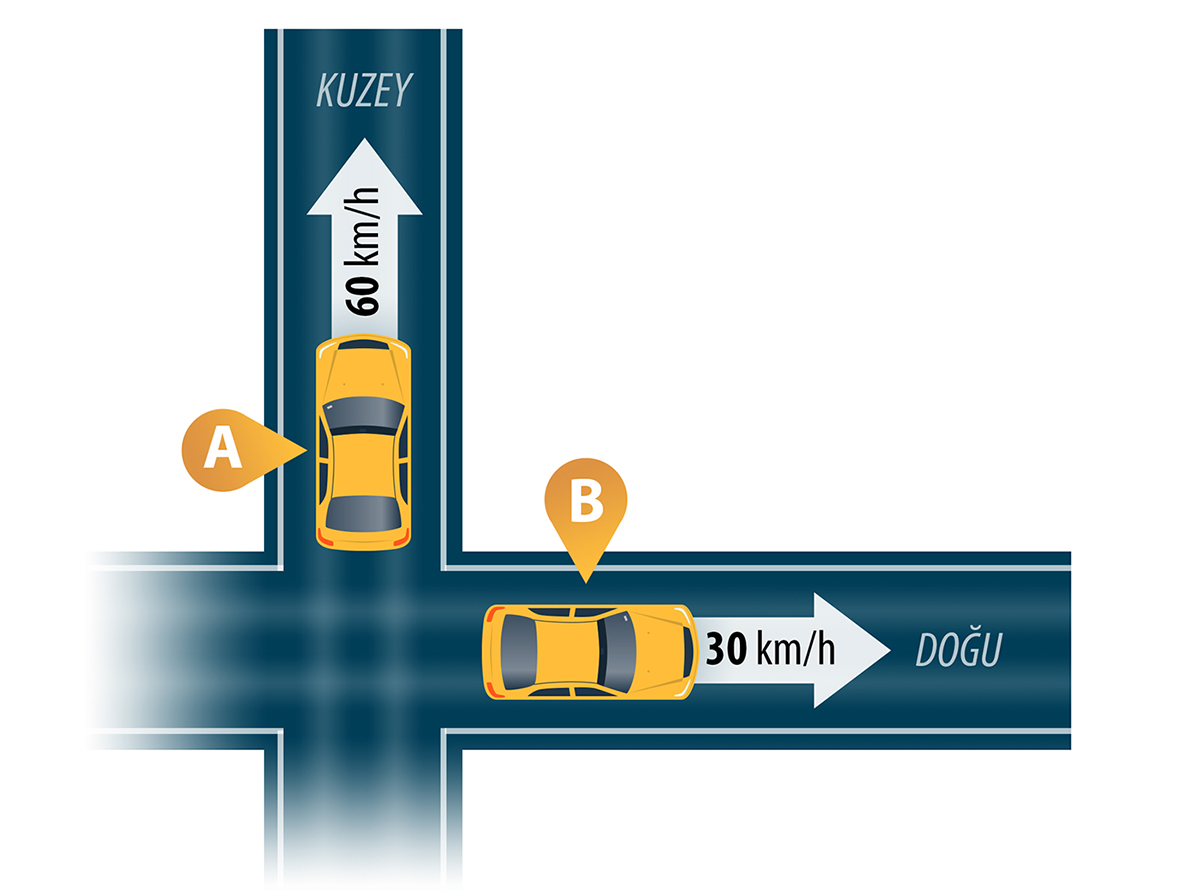
Bu iki aracın sadece hızlarının büyüklüğünü (sayısal değerini yani süratlerini) düşündüğümüzde bölme işlemini 60 km/h / 30 km/h = 2 kolayca yapabiliriz. Peki yönlerini nasıl birbirine böleceğiz? Bu, kuzey yönü içinde ne kadar doğu yönü olduğunu aramak gibi anlamsız bir şey olacağı için vektörlerle bölme işlemi yapamayız! Başka bir deyişle vektörlerle bölme işlemi tanımlı değildir.

Vektörel Nicelikler Nasıl Çarpılır?

Vektörlerin çarpımı ise skaler niceliklerle yapılan çarpma işleminden farklıdır. İki vektörü, yön özelliğini dikkate alarak iki şekilde çarpabiliriz: skaler çarpım ve vektörel çarpım. Bu isimlendirme, iki vektörün çarpımının sonucunun bir skaler mi yoksa bir vektör mü olacağına bağlı olarak tanımlanmıştır. Fizikte, iki vektörün çarpım sonucunun skaler (örneğin bir kuvvetin yaptığı iş) ve vektör (bir kuvvetin döndürme etkisi, tork) olarak tanımlandığı durumlar vardır. Skaler çarpımda çarpılacak iki vektörün sadece aynı doğrultudaki bileşenlerini işleme dâhil edip çarparız. Böylece aynı yöndeki niceliklerle işlem yaparak yön özelliğini ayıklamış oluruz ki bu da iki sayının skaler çarpımından başka bir şey değildir ve sonuç skaler bir sayıdır. Vektörel çarpımda ise iki vektörün sadece birbirine dik bileşenlerini işleme dâhil edip çarparak her iki vektörün yönüne dik yönde yeni bir vektör oluştururuz ki bu da yönlü olduğu için sonuç vektördür.

Vektörler Ne Zaman Kullanılır?

Peki vektörleri her zaman kullanmak zorunda mıyız? Bir boyutlu uzayda yaşıyor olsaydık vektörlere gerek kalmadan yönlü niceliklerin yönünü sadece (-) ve (+) işareti ile ifade edebilirdik. Çünkü bir boyutta, diyelim ki bir doğru üzerinde, bir cisim ya sağa (+) ya da sola (-) hareket edebilir. Örneğin bir boyutta hızı -30 km/h olan bir trenin 30 km/h büyüklüğünde bir hızla sola doğru hareket ettiğini anlarız. Ama iki boyutta (bir düzlemde) veya üç boyutta (uzayda) hareket eden cisimler tanımlarken vektörleri kullanmak gereklidir.

Peki, sadece vektörlerle yön içeren tüm nicelikleri tanımlamak yeterli olur mu? Pek değil! Bu gibi karmaşık durumları tanımlayabilmek için neleri kullandığımıza ise sonraki bir yazımızda değinebiliriz.

Kaynaklar:

• https://acikders.ankara.edu.tr/mod/resource/view.php?id=87
• fizikdersi.gen.tr/skaler-vektorel-buyuklukler-arasindaki-fark-nedir/

Yazar Hakkında:

Ankara Üniversitesi Fizik Mühendisliği Bölümü