Dairenin Alanını Hesapladığımız Formül Nereden Geliyor?

FilippoBacci/iStock.com

Bir önceki yazımızda herhangi bir noktadan eşit uzaklıktaki noktalar kümesinin yani çemberin çevre uzunluğunun 2πr’ye eşit olduğunu ispatladık. Bunun için çemberin içine tepe noktaları çemberin merkezinde bulunan sonsuz sayıda üçgen yerleştirdiğimizi varsaydık. Bu üçgenlerin oluşturduğu düzgün çokgenin çevre uzunluğunun çemberin çevre uzunluğuna yakınsayacağı bilgisini kullandık.

Benzer şekilde çemberin çevrelediği alan yani dairenin alanı da aynı yöntemle hesaplanabilir. Nasıl ki sonsuz sayıda üçgenin oluşturduğu düzgün çokgenin çevre uzunluğu çemberin çevre uzunluğuna yakınsıyorsa, bu üçgenlerin alanları toplamı da dairenin alanına yakınsar. 

Bunun için öncelikle dairenin içerisine n kenarlı düzgün bir çokgen yerleştirdiğimizi düşünelim. Bu n kenarlı düzgün çokgen aslında tepe noktaları dairenin merkezinde bulunan n adet birbirine eş üçgenden oluşur. 

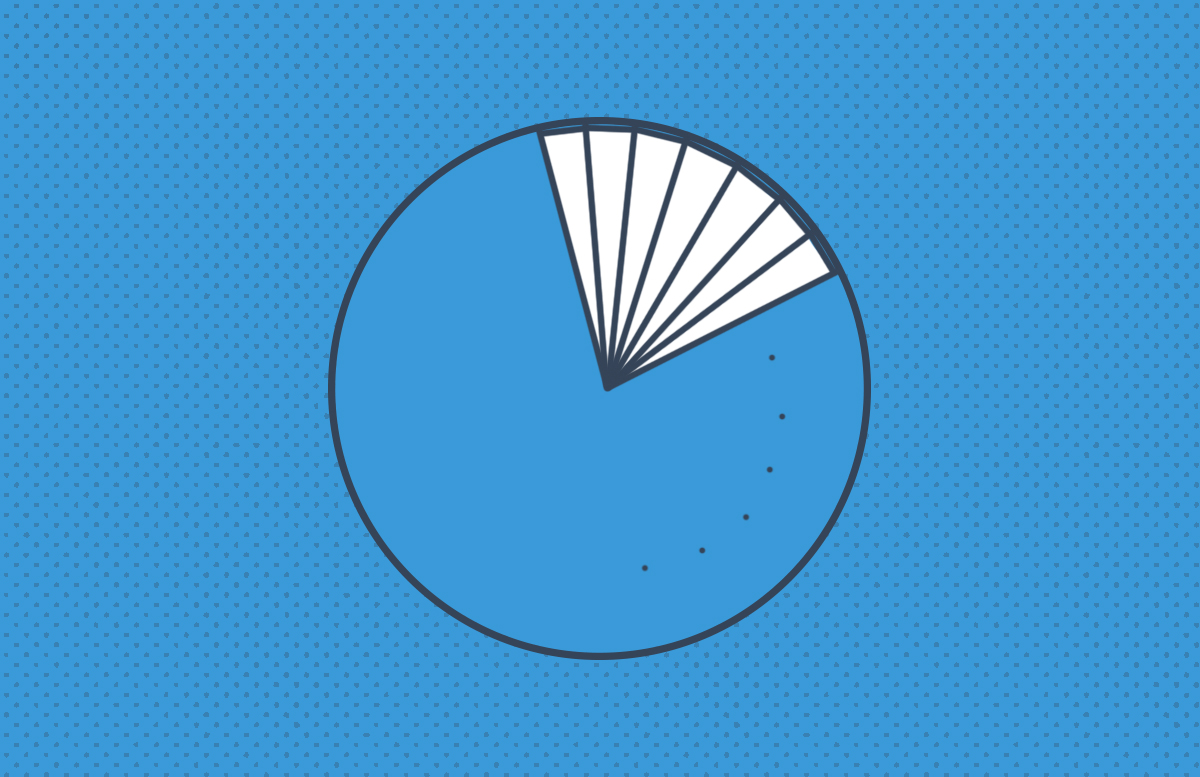
Yani tüm üçgenlerin taban uzunlukları ve kenar uzunlukları birbirine eşittir. Üçgenlerin taban uzunlukları “L”, kenar uzunlukları ise “r” birim olsun. 

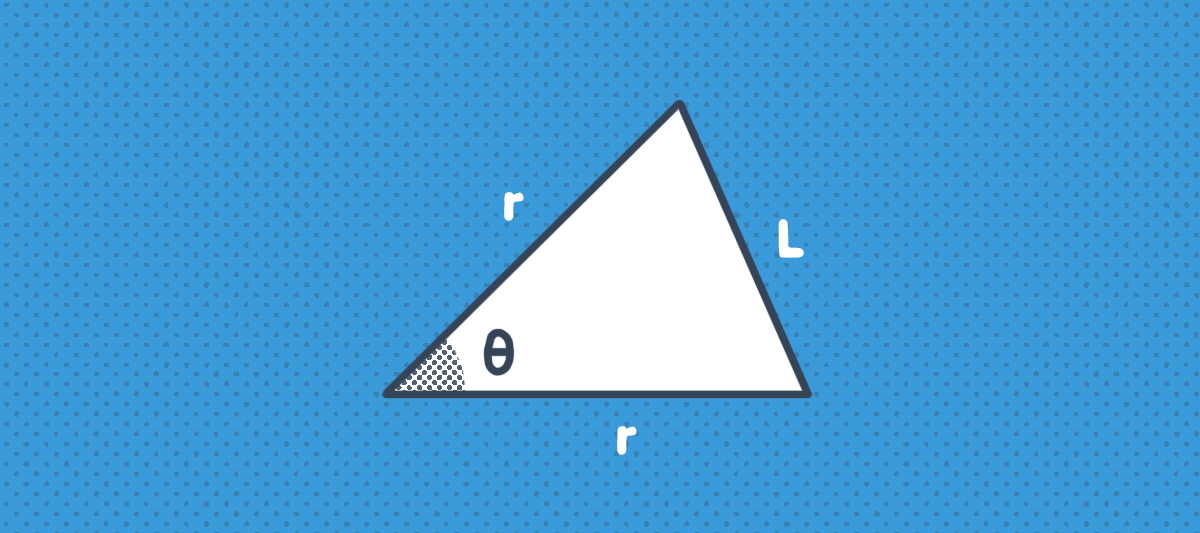
Her bir üçgenin tepe açısının ölçüsü θ=2π/n derecedir. Bu durumda her bir üçgenin alanı 

A= r2sin(θ)/2= r2sin (2π/n)/2 formülüyle hesaplanabilir. Dairenin içerisinde bulunan üçgenlerin sayısını ifade eden n çok büyük bir sayı olarak düşünüldüğünde, üçgenlerin alanları toplamı dairenin alanına yakınsar. Bu durumun matematiksel ifadesi

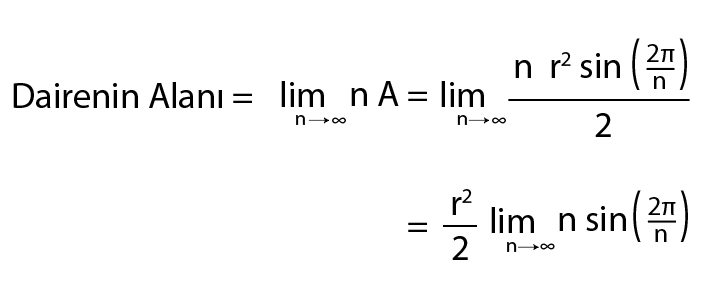
şeklindedir.

Yukarıdaki son eşitlikte r2/2 değeri, n sonsuza giderken bakılan limit değerinin kat sayısıdır.

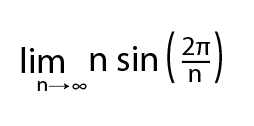ifadesinin değerinin ise 2π değerine yakınsadığı L’Hospital kuralı ile gösterilebilir.

Sonuç olarak dairenin alanı, D.A= πr2 olarak elde edilir.