Gauss’un Egregium Teoremi Nedir?

ullstein bild Dtl./Contributor/Gettyİmages

Pek çoğumuz Carl Friedrich Gauss’un ismini 1’den n’ye kadar olan doğal sayıları toplamaya çalışırken duymuşuzdur. Çocuk yaşta keşfettiği pratik toplama formülüyle dikkat çeken ve ilerleyen yıllarda “Matematikçilerin Prensi” olarak anılan bu dehaya biz kısaca ‘Gauss’ diyeceğiz.

Matematik dünyasına kazandırdığı Gauss toplam formülüyle (1+2+3+…+n=n(n+1)/2) adım atan Gauss, daha sonra yeryüzünün ölçümü üzerine araştırmalar yaparak yüzey geometrisine yöneliyor. Bu alanda yaptığı çalışmalar sonucunda ’olağanüstü’ ya da ’şaşırtıcı’ anlamlarına gelen Egregium Teoremi’ni keşfediyor. Gauss’un 19. yüzyılın ilk yarısında öne sürüp ispatladığı bu keşif daha sonraları haritacılıktan maden mühendisliğine, origami sanatından 3 boyutlu (3D) tarama teknolojilerine kadar pek çok yerde kullanılır hâle geliyor.

Gauss Egregium Teoremi’nin Temel Mantığı Nedir?

Bir maddenin şeklini tespit etmek ve yüzey türünü geometrik anlamda sınıflandırmak için ‘Gauss eğriliği’ denilen bir kavramdan yararlanılır. Eğrilikler düz bölgeler için 0, içbükey bölgeler için pozitif, dışbükey bölgeler için negatiftir. Bu değerleri bulup birbiri ile çarptığınızda Gauss eğriliğini hesaplamış olursunuz. Egregium Teoremi, Gauss eğriliğinin izometriler tarafından korunduğunu yani değişmediğini söyler. İzometriyi kabaca bir yüzeyi kesmeden veya esnetmeden diğerine dönüştürme özelliği olarak düşünebilirsiniz. Örneğin Gauss eğriliği 0 olan bir A4 kâğıdının görseldeki gibi bükülmesiyle oluşturulan şekil, A4 kâğıdının bir izometrisidir ve her iki durumda da kâğıtların Gauss eğriliği aynıdır.

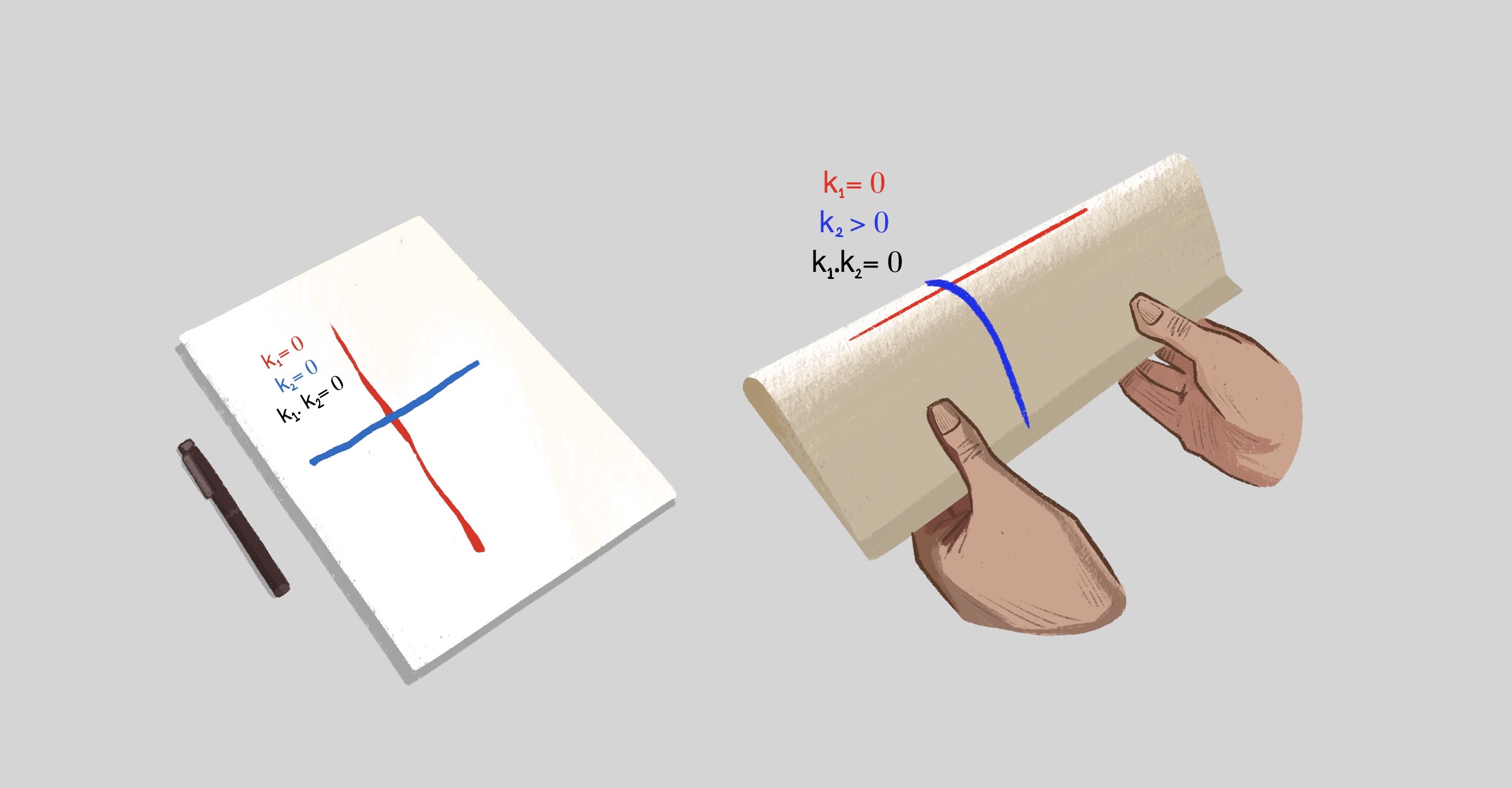
Her iki kâğıdın bölgesel olarak hesaplanan Gauss eğriliği sıfırdır.

Farklı bir örnek olarak bir esnek pilates topu düşünelim. Küresel topun Gauss eğriliği topun her yerinde sabit ve pozitiftir. Şimdi bu top üzerine hafif bastıralım. Ezilmiş topun Gauss eğriliği yine pozitiftir. Yani Egregium Teoremi, topun üzerine bastırılarak formu değiştirildiğinde bile top yırtılmadığı sürece Gauss eğriliğinin değişmediğini söyler.

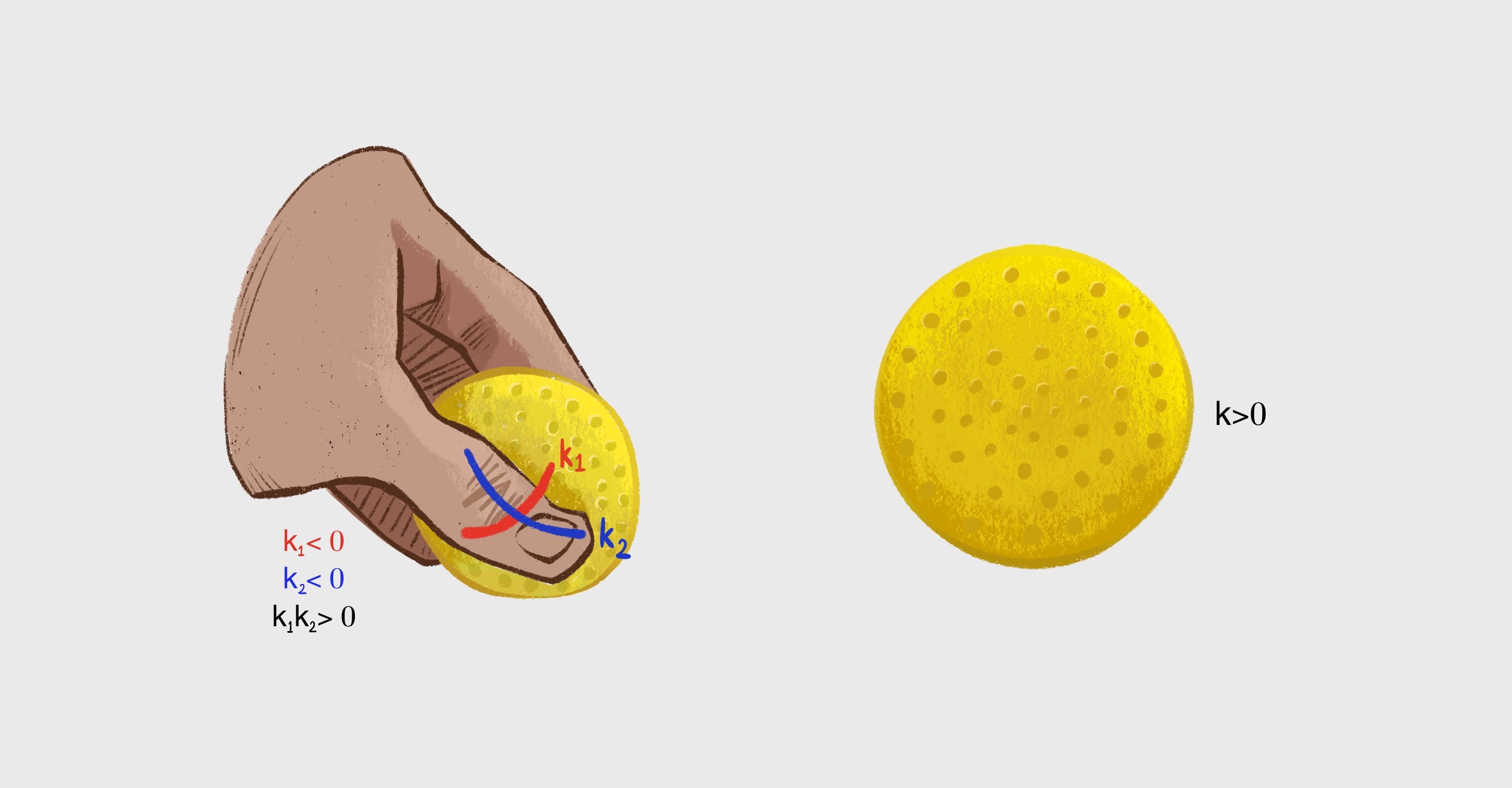
Her iki topun bölgesel olarak hesaplanan yüzey eğrilikleri birbirine eşittir.

Egregium Teoremi’nin Yüz Tanılamadaki Rolü Nedir?

ATM’ler ve banka kasaları gibi işlemlerin yüksek güvenlikli olarak yapılması gerektiği yerlerde 3D yüz tanılama özelliği yaygın olarak kullanılır. Yüzlerce kişi arasından aranan bir şahsı birebir eşleme yoluyla tanılamada da bu teknolojiden yararlanılır. Yüz tanılamadaki en büyük problem, insan yüzünün görünümünün ışık şartları, arka plan ve başın duruş pozisyonu gibi dış etkenlerden büyük oranda etkilenmesidir. Bunun yanı sıra saç şekli, kozmetik kullanımı, plastik cerrahi veya kilo kaybı gibi faktörler de yüzün görünümünü etkileyebilir. Yüzün görünümü farklı mimik hareketlerinden de etkilenebilir.

3D yüz tarama teknolojisi ile dijital ortama aktarılıp Gauss eğrilikleri, topolojisi ve genel geometrik yapısı kaydedilen bir yüz düşünelim. Egregium Teoremi’ne göre bu eğrilikler sadece yüzün iç geometrisine bağlı olduğu için kişinin kafa pozisyonu, yüzünü eğip bükmesi, ışıklandırma koşulları altında bile yüzün Gauss eğriliğinde hiçbir şey değiştirmiyor. Hatta sistem her bir yüz ifadesini birbirine izometrik yüzeyler olarak algılıyor ve eşleştirme yapıyor.

ChatGPT

Her iki resimde de bölgesel olarak ölçülen yüzey eğrilikleri aynıdır.

Egregium Teoremi’ndeki İzometriyi Bozan Durumlar Var mı?

Pilates topu örneğinde, üzerine bastırarak topta oluşturduğumuz form değişimi ile topun yüzey eğriliğinin değişmeyeceğinden bahsetmiştik.

İnsan yüzündeki her bir ifadenin birbirine matematiksel anlamda denk bölgesel izometriler oluşturduğundan da bahsetmiştik. Ancak ağız açık olduğunda yüzde bir delik oluştuğundan bu durum, yüzün topolojisini değiştirir. Bu da istenmeyen bir durumdur.

Özetle Gauss’un Egregium Teoremi, yüz tanıma algoritmalarının yüzün farklı pozisyonlar ve deformasyonlar altında bile doğru sonuçlar vermesini açıklayan bir teoremdir. 19. yüzyıldaki keşfiyle 21. yüzyıldaki teknolojik gelişmelere de ışık tutan Carl Friedrich Gauss “Matematiğin Prensi” lakabının hakkını vermiştir.

Eşleştirme tamam!

Kaynaklar:

• Doğan,S., “Bir Riemann Manifoldunun Eğrilikleri ve Uygulamaları”, Y. Lisans Tezi, İnönü Üniversitesi, s. 67, 2008.
• https://www.cs.technion.ac.il/wp-content/ron-kimmel/papers/BroBroKimIJCV05.pdf, sf 3-5
• Kamberov George and Gerda, “Shape Invariants and Principal Directions from 3D Points and Normals”, Hofstra University, Conference Paper, January 2002, USA, s. 6.

Yazar Hakkında

Saadet Doğan

Aydın Nova Akademi Matematik Öğretmeni