GeoGebra ile Bir Üçgende Açıortay-Kenarortay-Yükseklik İlişkisi

Açılar ve kenarlar, üçgenlerin temel elemanları; yükseklik, açıortay, kenarortay ve orta dikmelerse yardımcı elemanlarıdır. Bu elemanların tanımları ve özellikleri kolay anlaşılır olsa da aralarındaki ilişkiler oldukça karmaşıktır. Mesela bir üçgende bir açı değiştiğinde temel elemanlar ve yardımcı elemanlar nasıl etkilenir? Ya da herhangi bir üçgende bu elemanlar arasında nasıl ilişkiler vardır? Şimdi bu sorunun cevabını bulmaya çalışalım.

Bir şekli kendisine göre simetrik iki eş parçaya ayıran doğruya simetri ekseni, bir açının simetri eksenine ise açıortay (veya açıortay doğrusu) denir (Şekil 1). Kenarortay, bir köşeden karşısındaki kenara çizilen ve kestiği kenarı iki eş parçaya ayıran doğru parçasıdır (Şekil 2). Bir üçgenin herhangi bir köşesinden karşı kenarına indirilen dik doğru parçasınaysa o kenara ait yükseklik denir (Şekil 3).

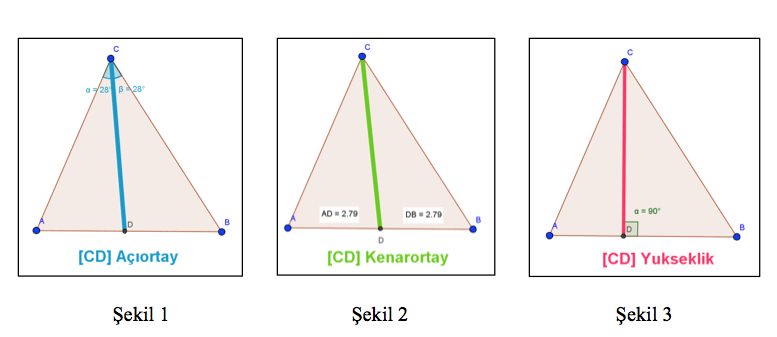
Belirli bir üçgenin açıortay, kenarortay ve yükseklik uzunlukları hakkında çıkarım yapmak kolay olsa da bu yardımcı elemanların herhangi bir üçgendeki uzunlukları hakkında bir genelleme yapmak zordur.

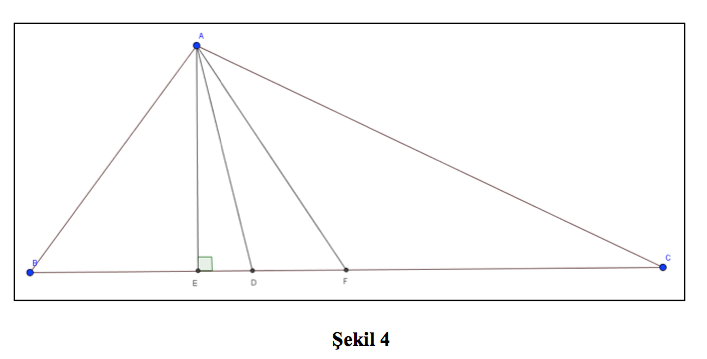
Rastgele bir ABC üçgenini ele alalım ve bu üçgenin [BC] kenarına ait yardımcı elemanları arasındaki ilişkiyi inceleyelim (Şekil 4). Düzlemdeki bir noktadan bir doğru parçasına giden en kısa uzaklık, bu noktadan doğru parçasına indirilen dikmedir. Bu dikme, ABC üçgeninin aynı zamanda [BC] kenarına ait yüksekliğidir. Dolayısıyla, A noktasından [BC] kenarına çizilen her doğru parçası yükseklikten daha eğik yani daha uzun olacaktır. Buradan hareketle, A noktasından [BC] kenarının yüksekliğinin bu kenara ait açıortay ve kenarortaydan daha kısa olduğunu söylemek mümkündür. [AB] uzunluğunun [AC] uzunluğundan daha kısa olduğunu kabul ederek açıortay ve kenarortay arasındaki ilişkiyi açıklamaya çalışalım. Verilen AED üçgeninde EAD açısının ölçüsü α olsun. Bu durumda, bir dış açının ölçüsü kendisine komşu olmayan iki iç açının ölçüleri toplamına eşit olması kuralından dolayı, ADF açısının ölçüsünün 90+α olduğu bulunur. Diğer bir deyişle, ADF açısı geniş bir açıdır ve ölçüsü DAF ve AFD açılarından daha büyüktür. Dolayısıyla, AFD üçgenini ele aldığımızda büyük açının karşısında uzunluğu büyük olan kenar bulunur bağıntısından yola çıkarak [AF] uzunluğunun [AD] uzunluğundan büyük olduğu sonucuna ulaşırız. Yani A köşesine ait kenarortay, açıortaydan büyüktür. Sonuç olarak, verilen bir ABC üçgeninde kenarortayın açıortaydan, açıortayın da yükseklikten büyük olduğu sonucunu elde ederiz. Peki, bu ilişki herhangi bir üçgen için de doğru mudur? GeoGebra yazılımını kullanarak bu soruya cevap bulabiliriz.

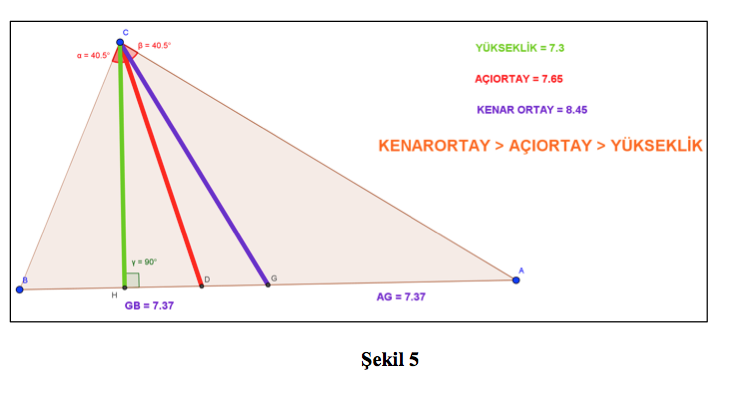
GeoGebra programını kullanarak rastgele bir üçgen çizelim (Şekil 5). Buradan dik doğru araç çubuğunu kullanarak C köşesine ait yüksekliği, açıortay araç çubuğunu kullanarak BCA açısının açıortayını ve orta nokta araç çubuğunu kullanarak [AB] doğru parçasının orta noktasını bulabiliriz (https://www.geogebra.org/o/quvEwgux). Bu doğru parçalarının uzunluklarını bulduktan sonra “KENARORTAY>AÇIORTAY>YÜKSEKLİK” eşitsizliğinin sağlandığını görürüz. Bu örnek de daha önce yaptığımız gibi sadece rastgele çizdiğimiz bir üçgen için doğruluğu gösterir. Fakat burada dinamik matematik yazılımının sürükleme özelliği sayesinde bu eşitsizliğin oluşturacağımız herhangi bir üçgen için de doğru olacağını gösterebiliriz.

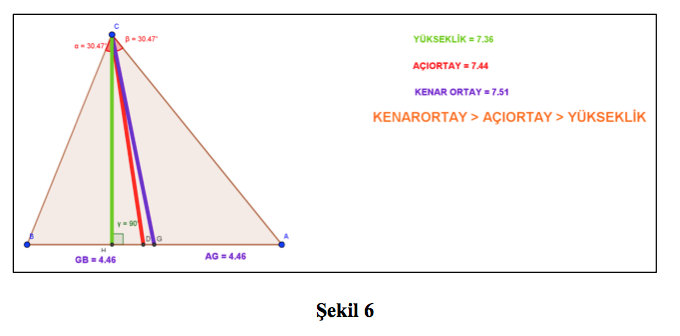
A noktasını seçip sola doğru sürüklediğimizde (Şekil 6) oluşan şekil hâlâ eşitsizliğin doğru olduğunu gösterir (https://www.geogebra.org/o/gJnz7Szh). A noktasındaki değişimle beraber üçgenin kenar uzunlukları ve açıları değişirken, eş zamanlı olarak bu kenar uzunluklarının değişimi de sağ tarafta gözlemlenebilir. Bu sürükleme işlemini sonsuz sayıda üçgen için yapabiliriz. Seçilen herhangi bir üçgende ne kadar değişiklik yaparsak yapalım bu eşitsizlik doğru olacaktır. Birçok kişi için ispatlaması ya da çıkarım yapması hayli zor olan “bir üçgendeki yükseklik, açıortay ve kenarortay ilişkisi” GeoGebra programının görselliği sayesinde kolayca anlaşılabiliyor. Programın görsel özellikleri soyut bir algının somut bir algıya dönüşmesine katkı sağlıyor.

Rastgele üçgenler seçtiğimizde böyle bir durum söz konusuyken, özel üçgenlerdeki durumu da inceleyelim. Daha önce üzerinde çalıştığımız üçgeni, köşelerinden sürükleyerek eşkenar üçgen haline dönüştürürsek (https://www.geogebra.org/o/J8trCqYW), kenarortay, açıortay ve yüksekliklerin birbirine eşit olduğu sonucuna ulaşırız. Diğer bir deyişle, bir eşkenar üçgende yükseklik, açıortay ve kenarortay birbirine eşittir önermesinin doğruluğunu göstermiş oluruz (Şekil 7).

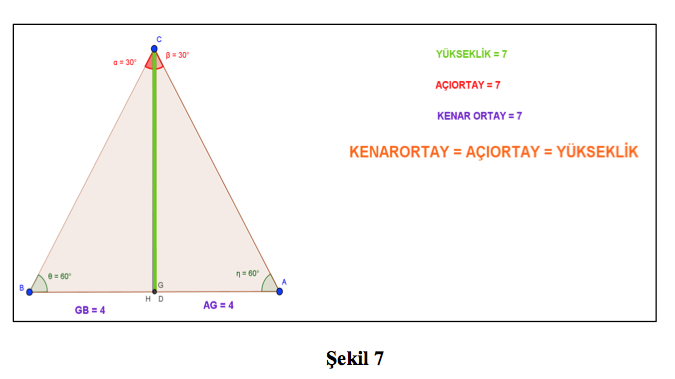
Aynı eşitlik herhangi bir ikizkenar üçgen için de geçerlidir. Yine verilen üçgen(ler)de köşeleri sürükleyerek bir ikizkenar üçgen elde ettiğimizde (https://www.geogebra.org/o/NRWAKeau), yükseklik, açıortay ve kenarortayın birbirine eşit olduğunu gözlemleriz (Şekil 8).

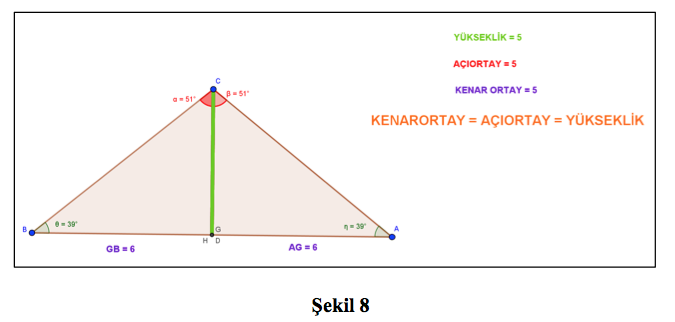
Görüldüğü üzere GeoGebra programı sayesinde bir üçgenin yardımcı elemanları arasındaki ilişkiyi öğrenmek kolaylaştırılabilir. Özellikle rastgele seçilen bir çeşitkenar üçgende bu ilişkiyi anlamak için uzunluklar bulunup “KENARORTAY>AÇIORTAY >YÜKSEKLİK” eşitsizliği elde edildikten sonra, herhangi bir köşenin sürüklenmesiyle beraber, üçgenin kenar uzunlukları ve açıları değişmesine rağmen, “KENARORTAY>AÇIORTAY >YÜKSEKLİK” eşitsizliğinin korunduğunun görülmesi bu yardımcı elemanlar arasındaki ilişkiyi anlamayı kolaylaştıracaktır. Diğer bir deyişle, bu eşitsizliğin seçilen herhangi bir çeşitkenar üçgen için her zaman doğru olduğunu görmeyi sağlayacaktır. Dinamik matematik yazılımı GeoGebra ile geometride görmekte veya genelleme yapmakta zorluk çektiğimiz durumları görselleştirerek, kolayca anlayabiliriz. GeoGebra programının bu dinamiklik özelliğini kullanarak başka hangi ilişkilerin, önermelerin ve teoremlerin doğrulunu kolayca öğrenebiliriz sorusunun cevabını siz sevgili okuyucularımıza bırakıyoruz.