GeoGebra ile Dik Üçgen ve Trigonometrik Oranlar

Trigonometri, birçok kişinin korkulu rüyası olmuştur. “Sinüs hangi bölgede hangi işareti alır?”, “Kosinüs ne zaman artar, ne zaman azalır?” gibi sorulara verilen cevaplar çoğu kişi için ezber kavramlardan öte gidememiştir. Peki, nedir bu soruların cevapları? Aslında hepsi çok basit, hepimizin iyi bildiği bir kavrama dayanıyor: üçgen.

Üçgen, ülkemizdeki öğretim programlarında ve kitaplarda “aynı doğru üzerinde olmayan üç noktayı birleştiren doğru parçalarından meydana gelen kapalı geometrik şekil” olarak tanımlanıyor. Peki, nedir bu kapalı şekil, çeşitleri nelerdir, kenarları ve açıları arasında nasıl bir ilişki vardır? Mevcut kitaplarda ve öğretim programlarının çoğunda bu sorulara cevap verilirken sabit (durağan) bir üçgen şekli kullanılır; üçgenin dinamik yapısından ve özelliklerinden ise hayli az bahsedilir. Örneğin 30^o-60^o-90^o, kenarları 1, √3, 2 sayıları ile orantılı olan çoğumuzun bildiği özel bir dik üçgeni ele alalım. Bu özel üçgen ile ilgili bir soruyla karşılaştığımızda, çoğumuz bu sayıları ezberleyerek çözüme ulaşmaya çalışırız, ama kaçımız bu sayıları dik üçgeni kullanarak kolayca bulabileceğimizi biliyor?

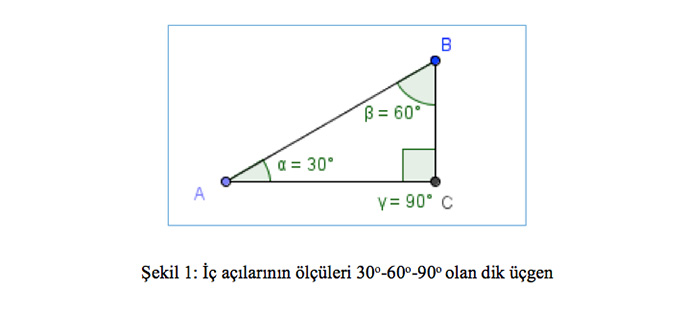
30^o-60^o-90^o dik üçgeniyle ilgili (bkz. Şekil 1) şu sorunun cevabını kalem ve kâğıt kullanmadan düşünelim: “Bu üçgendeki dik üçgeni koruyarak, 30 derece olan alan açıyı 35 dereceye çıkardığımızda, üçgenin diğer açıları ve kenarları nasıl değişir?” Bu soruyu sorduğum lisedeki bazı öğrenciler dik açıyı koruyarak dediğim halde, dik açıyı 85 dereceye düşürüp 30 derecelik açıyı 35 dereceye çıkardılar ve 60 derecelik açıyı korudular. Bazıları da “Hipotenüs değişmez çünkü karşısındaki açı değişmedi” , “AB uzunluğu artar çünkü karşısındaki 30 derecelik açı 35 dereceye çıkarıldı” ya da “BC uzunluğu azalır çünkü karşısındaki açının ölçüsü 60 dereceden 55 dereceye düştü” gibi karşılıklı açı ve kenarlar arasındaki ilişkiye dayanarak çıkarımlarda bulundu, fakat kullandıkları matematiksel bilgi yanlış sonuçlar doğurdu. Belki sizin de benzer yaklaşımlarınız olmuştur soruya. Kalem ve kâğıt kullanarak soruyu cevaplamalarını istediğimde ise, yine benzer cevapları verdiler ve sonuca ulaşamadılar. Öğrencilerin bu yanlış çıkarımlarını düzeltmek ve konuyu onlara daha iyi öğretebilmek için, GeoGebra dinamik matematik yazılımının özelliklerinden faydalanılabilir.

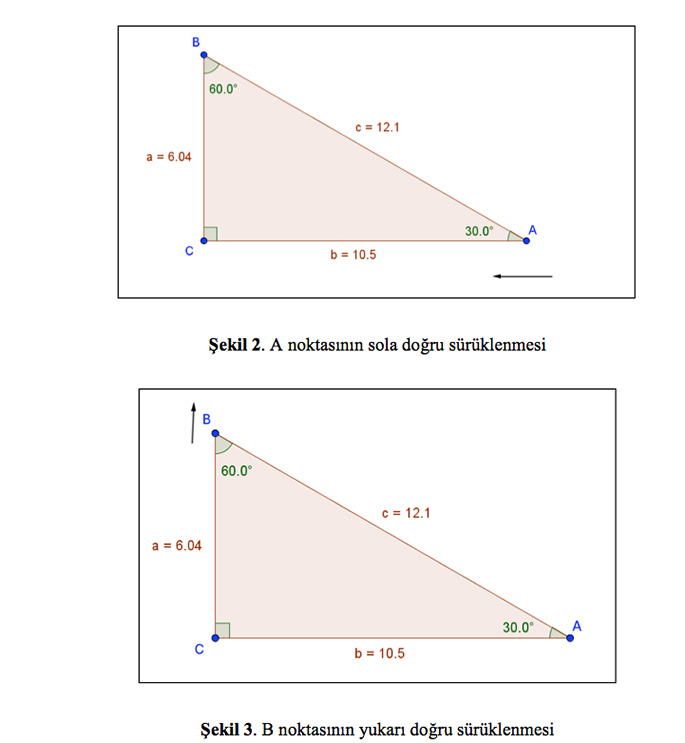
GeoGebra programında, açıları 30^o-60^o-90^o olan bir dik üçgen çizerek 30 derece olan açının ölçüsünü 35 dereceye çıkaralım (http://tube.geogebra.org/student/m2594217 ). 30 derecelik açıyı 35 dereceye çıkarmak için iki seçeneğimiz var. Öncelikle, A noktasını seçip sol tarafa doğru sürükleyerek (bkz. Şekil 2) açıyı 35 dereceye çıkarabilirsiniz. Bu artışla beraber, BC doğru parçasının uzunluğunun değişmediğini, AB ve AC doğru parçalarının ise eş zamanlı olarak azaldığını gözlemleyebilirsiniz. İkinci bir seçenek olarak, B noktasını seçip yukarıya doğru sürükleyebilirsiniz (bkz. Şekil 3). Burada da, AC doğru parçasının uzunluğunun değişmediğini, BA ve BC doğru parçalarının uzunluklarının ise eş zamanlı olarak arttığını gözlemleyebilirsiniz. Görüldüğü üzere GeoGebra programı, bir dik üçgenin temel elemanlarından biri değiştiğinde, diğer temel elemanlarda oluşacak eş zamanlı değişimleri bulmayı ve yorumlamayı kolaylaştırabilir.

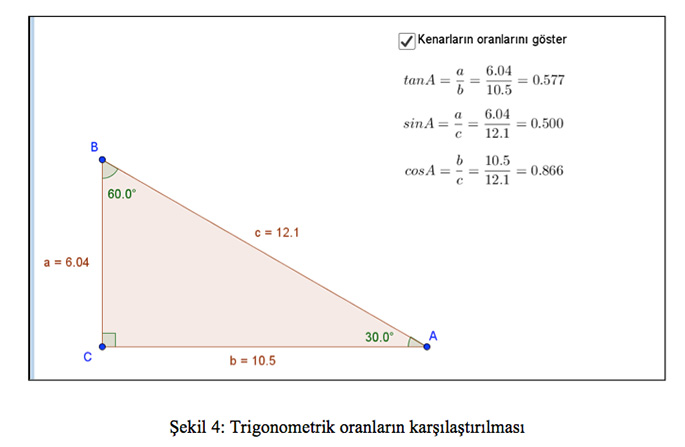
Yazının başında trigonometrinin temelinin üçgenlere dayandığından bahsetmiştik. Peki, sinüs ve kosinüsteki değişimi bu dik üçgeni kullanarak nasıl anlatabilirim? Üçgenler aynı zamanda trigonometrinin temeli olduğundan sinüs, kosinüs, tanjant ve kotanjantın açıya bağlı olarak artması ya da azalması dik üçgenler kullanılarak anlatılabilir. Sinüs, “bir dik üçgende karşı kenarın hipotenüse oranı” olarak tanımlanır. Dolayısıyla ben bu üçgeni kullanarak “Sinüs 35 mi yoksa sinüs 30 mu daha büyüktür?” sorusunu kolayca cevaplayabilirim. Bunun için de bu değerlere karşılık gelen kenarların oranlarını karşılaştırmam yeterlidir. GeoGebra programı yardımıyla bu etkinliği çok basit bir şekilde yapabiliriz (http://tube.geogebra.org/student/m2594463 ). Öncelikle, bu değerleri programı kullanmadan karşılaştıralım, daha sonra verilen linkteki pencerede yer alan “Kenarların oranlarını göster” kutucuğunu işaretleyerek trigonometrik oranlardaki değişimi gözlemleyelim ve cevaplarımızı karşılaştıralım. Eğer cevabımız doğru değil ise, neden doğru olmadığını GeoGebra programını kullanarak keşfetmeye çalışalım. Görüldüğü gibi, GeoGebra programıyla, dik üçgenin temel bir elemanının, örneğin bir açının değişmesiyle beraber sinüs, kosinüs, tanjant gibi trigonometrik oranlardaki değişimi gözlemleyerek (bkz. Şekil 4) bu değerleri kolaylıkla karşılaştırabiliriz.

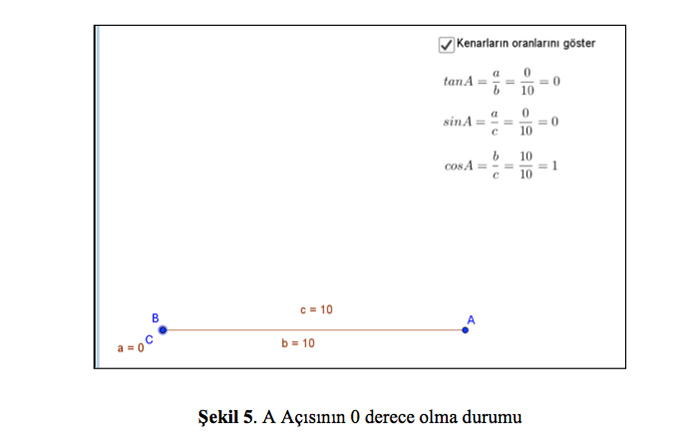
Yine trigonometri konusunda çoğu kişinin ezberlemeyi tercih ettiği sinüs 0^o= 0, kosinüs 0^o=1, tanjant 0^o=0, tanjant 90^o=∞ gibi bazı değerler var. Bu değerleri linkte verilen üçgeni kullanarak basitçe keşfedebiliriz. Örneğin A açısını temel alalım. A açısını 0 derece yapmak için, B noktasını sürükleyerek C noktasına yaklaştırdığımızda, bu trigonometrik oranları kolaylıkla hesaplayabiliriz ve penceredeki “Kenarların oranlarını göster” kutucuğunu işaretleyerek tahminlerimizin doğru olup olmadığını görebiliriz (bkz. Şekil 5). Sinüs 0’ı hep birlikte bulalım: Sinüs A karşı kenarın uzunluğunun hipotenüsün uzunluğuna oranıdır, yani a/c’dir. A açısını 0 derece olarak kabul ettiğimizde a kenarının uzunluğu da 0 olacaktır. Bu durumda sinüs A, a’nın hipotenüse (c’ye) oranı 0/10 şeklinde tanımlanacaktır. Matematikte 0’ın bir sayıya oranı 0 olduğu için sinüs A yani sin 0, 0’a eşittir diyebiliriz. Aynı şekilde kosinüs 0, tanjant 0, kotanjant 0, sinüs 90, kosinüs 90, tanjant 90, kotanjant 90 ve benzeri trigonometrik oranların da bu açı ölçülerine karşılık aldığı değerler kolaylıkla hesaplanabilir.

Birçok kişinin öğrenmede zorlandığı ve sadece ezberlenebilecek kavramlar olarak görülen trigonometrik oranlardaki değişim ve bazı önemli trigonometrik değerler, görüldüğü gibi GeoGebra programı kullanılarak basitçe öğrenilebilir. “Sinüs 30 mu yoksa sinüs 60 mı daha büyüktür?”, “Kosinüs 0 ile 90 derece arasında nasıl değişir?”, “Tanjant 45 neden 1’e eşittir?”, “Kosinüs 0’ın değeri nedir?”,  “Tanjant 90’ın değeri nedir?” gibi soruların cevaplarını verilen link yardımıyla kolayca keşfedebilirsiniz. Ayrıca, “GeoGebra programının bu dinamiklik özelliğini ve üçgenleri kullanarak başka hangi karmaşık konuları kolayca öğrenebiliriz?” sorusunun cevabını ise siz sevgili okuyucularımıza bırakıyoruz.

Kaynaklar:

• Moore, K. C., “Making sense by measuring arcs: A teaching experiment in angle    measure”, Educational Studies in Mathematics Education, Cilt 83, Sayı 2, s. 225-245, 2013.
• Thompson, P. W. ve ark, “ ‘The design of tasks in supportof teachers’ development of coherent mathematical meanings”, Journal of Mathematics Teacher Education, Cilt 10, Sayı 4-6, s. 415-432, 2007.
• Yigit, M., Learning of Trigonometry: An Examination of Pre-Service Secondary Mathematics Teachers’ Trigonometric Ratios Schema, Yayınlanmamış Doktora Tezi: Purdue Üniversitesi, West Lafayette, IN, Amerika Birleşik Devletleri, 2014.
• Yigit Koyunkaya ve ark, “Dynamic Right Triangles”, Mathematics Teacher, Cilt 109, Sayı 4, s. 320, 2015.