Güvercin Yuvası İlkesi Nedir?
10 adet güvercin 9 farklı yuvaya yerleştirildiğinde en az bir yuvada 1’den fazla güvercin bulunur. Günlük hayatta karşılaşabileceğimiz bir durum olan bu önerme matematikte “güvercin yuvası ilkesi” olarak bilinir. Anlaşılması basit olan bu önerme aslında oldukça zor problemlerin çözümünü sağlar. Gelin bu önermeyi daha ayrıntılı inceleyelim.

Çizim: Umut Aybek
10 adet güvercin 9 farklı yuvaya yerleştirildiğinde en az bir yuvada 1’den fazla güvercin bulunur. Günlük hayatta karşılaşabileceğimiz bir durum olan bu önermede mantık açısından herhangi bir problem yoktur. Matematikte “güvercin yuvası ilkesi” olarak bilinen önerme daha genel olarak şöyle ifade edilir: “N” adet güvercin “k” farklı yuvaya yerleştirildiğinde [(N/k)’nin bir tam sayı olmadığı durumda], en az bir yuvada (N/k) değerinden daha fazla güvercin bulunur.
Yukarıda verilen örnekte N değeri 10 (N=10), k değeri ise 9 (k=9)’dur. Güvercin yuvası ilkesindeki önermeye göre, en az bir yuvada 2 adet güvercin bulunduğu kolayca görülebilir: [2>(10/9)].
Güvercin yuvası ilkesi olarak bilinen önerme birçok zor problemin çözülmesini sağlar. Gelin şimdi bu sorulardan birkaçını birlikte inceleyelim.
Soru 1: 15 kişilik bir grubumuz olsun. Bu gruptan en az kaç kişi seçilmelidir ki seçilenlerden en az ikisi aynı ayda doğmuş olsun?
Doğru cevabın 13 olduğunu hemen bulabiliriz. Çünkü ilk 12 kişi on iki farklı ayda doğmuş olsa bile seçilecek son kişi ile gruptaki en az iki kişinin aynı ayda doğmuş olması garantilenir.
Şimdi inceleyeceğimiz soru ise biraz daha zor. Ama güvercin yuvası ilkesi yardımıyla kolayca çözülebilir.
Soru 2: Kenar uzunluğu 1 birim olan kare bir alan üzerine 51 farklı nokta yerleştirilir. Noktalar nasıl yerleştirilirse yerleştirilsin en az üç noktanın yarıçapı 1/7 olan bir dairenin içinde kalacağını gösterelim.
Karenin her bir kenarını görseldeki beş eşit parçaya bölelim ve bunlardan diğer kenarlara paralel doğrular çizerek kareyi 25 adet küçük eş karelere ayıralım.
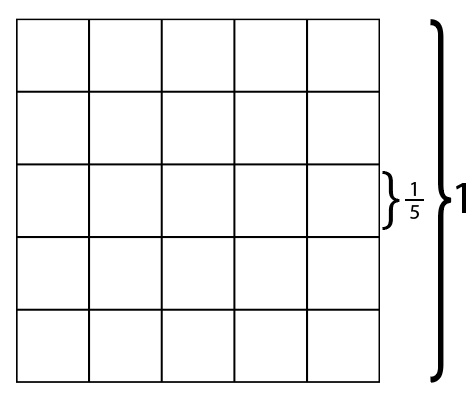
Güvercin yuvası ilkesindeki önermeye göre N değeri 51, k değeri ise 25 olur. Yani 51 nokta 25 farklı kareye yerleştirilmek isteniyor. Bu durumda küçük karelerden en az bir tanesinde (2<51/25<3 olduğu için) en az üç nokta bulunur.
Bu üç noktanın bulunduğu küçük karenin çevrel çemberini çizdiğimizde çemberin çap uzunluğu karenin köşegen uzunluğuna yani √2/5’e eşittir. Yarıçap uzunluğunun ise bunun yarısına yani r=√2/10=1/(5√2)’ye eşit olduğunu buluruz.

r= 1/(5√2) < 1/7 olduğu için bu kare içerisindeki üç nokta yarıçapı 1/7 olan bir daire içerisinde kalır.
Çözümü zor olan problemler oldukça basit bir önerme olan güvercin yuvası ilkesiyle çözülebilir. Daha farklı soruları da kendiniz araştırıp nasıl çözüleceğini keşfedebilirsiniz.
Kaynak: