Hayatımız Problem!

Matematik problemsiz olmaz, tıpkı hayat gibi. Bu cümleden ne anlıyoruz? Matematiğin başımıza dert olduğunu mu? Matematikte karşımıza çıkan problemlerin günlük hayatta karşılaştığımız problemlerden farkı nedir?

Burada “problem” kelimesinin anlamı üzerinde düşünmemiz gerekiyor. Bir çözüme veya sonuca varmamızı gerektiren herhangi bir durum düşünelim. Eğer çözüme veya sonuca varmak için ilk bakışta belirgin bir yol göremiyorsak bu durumu “problem” olarak adlandırabiliriz. Günlük hayatta karşılaştığımız bazı problemleri çözebilmek için de matematik bilgilerimizi kullanmamız gerekebilir.

Problem denince aklıma ilk gelen -matematiği çok sevdiğim için- matematik problemleri oluyor. Öğrenci olduğumuz zamanlardan beri karşımıza çıkan bazı meşhur problem türleri var: havuz problemleri, işçi problemleri, yaş problemleri, dört işlem problemleri... Günümüzde bunlara yenileri eklendi. Geçenlerde internette dolaşırken ilk defa mum problemleri ve kuyruk problemleri gibi değişik türde problemler gördüm. Nedir bu havuzlardan çektiğimiz? Ya da havuzların bizden çektiği? Neden bir musluk havuzu doldururken diğer taraftan havuzu boşaltmaya çalışırız mesela? Ya da 3 kişinin 5 günde ancak yapabildiği işi neden tek bir işçiye daha uzun sürede yaptırmak isteriz? Aslında bu tür problemlerin hepsinin arkasında bir matematiksel fikir var. Örneğin havuz ve işçi problemleri ters orantı kavramı ile ilgilidir. Yaş problemleri -hani şu “Annenin yaşı kızının yaşının 2 katının 10 fazlasıdır.” benzeri ifadeler içeren sorular- cebirsel ifade yazma ve denklem kurma becerisini geliştirme-ölçme amacı taşır. Bu tür sorularda sürekli benzer bağlamlar (soru hikâyesi) kullanılınca artık bu adlarla anılmaya başlandılar. Böyle çok sayıda örnekle karşılaşmış biri için problem çözümünde izlenecek yol bellidir; sadece bildiği bir yöntemi problem şartlarına uyarlaması gerekecektir. Bu tür problemleri “rutin” veya “sıradan” problemler olarak adlandırabiliriz.

İçinizde daha önce hiç “havuz problemi” ile karşılaşmamış olan biri için bu yeni bir durumdur ve çözüm için kendisinin yeni bir yöntem geliştirmesi gerekecektir. Bu kişi için karşılaştığı durum “rutin olmayan” veya “sıra dışı” bir problem olacaktır.

Ben matematik meraklısı biri olarak matematiksel keşifler yapabileceğim, benim için sıra dışı olan problemler ile uğraşmayı seviyorum. Sadece doğru sonucu bulmak değil, o sonuca nasıl ulaşıldığı ve sonucun neden doğru olduğu ile de ilgileniyorum. O yüzden problemi çözdükten sonra geriye dönüp “Başka yollardan da çözebilir miydim?”, “Problemde verilen durum şu şekilde değişseydi sonuç nasıl etkilenirdi?” gibi sorular soruyorum. Bu sayede ilginç bağıntılar ve ilişkiler ortaya çıkabiliyor.

Her ne kadar problem çözerken izleyeceğim yolu kendim belirlemek istesem de probleme yaklaşımımda bazı stratejiler (taktikler) kullanmak işime yarıyor. İki matematik eğitimcisi Alfred Posamentier ve Stephen Krulik tarafından önerilen problem çözme stratejileri şunlardır:

• Geriye doğru çalışma

• Örüntü/bağlantı bulma
• Farklı bir bakış açısı benimseme
• Benzer, daha basit bir problem çözme
• Özel/uç durumları göz önünde bulundurma

• Görsel temsil kullanma (resim/diyagram çizme)
• Akıllı tahmin ve kontrol yapma
• Tüm durumları listeleme

• Verileri düzenleme

• Mantıksal akıl yürütme

Problem çözerken çeşitli aşamalarda bu stratejilerden bir veya birkaç tanesini kullanabiliriz. Örneğin problemi daha iyi anlayabilmek için bir şekil çizebiliriz veya problemdeki verileri bir tablo yardımıyla düzenleyebiliriz. Çözüm aşamasında olası durumları sistematik bir şekilde listelemek örüntüleri daha rahat görmemizi sağlayabilir.

Şimdi örnek problemler üzerinde çalışalım.

Problem 1: Defne’nin 5 matematik testinden aldığı notların ortalaması 70 olsun. Öğretmen dönem sonunda her öğrenci için, o öğrencinin en düşük not aldığı testi değerlendirme dışı bırakıp 4 test üzerinden yeni ortalama hesaplıyor. Defne’nin yeni not ortalaması 75 olduğuna göre, değerlendirme dışı kalan testten kaç puan almıştır?

Burada okumaya devam etmeden önce problem üzerinde düşünmenizi rica ediyorum.

Bu problemde “geriye doğru çalışma stratejisi” kullanılabilir. Sondan başlayarak düşünelim: 4 testin not ortalaması 75 ise Defne’nin bu testlerden aldığı notların toplamı 4’e bölündüğünde sonuç 75 çıkmış demektir. O zaman notların toplamı 75x4=300’dür. Aynı şekilde 5 testin ortalaması 70 ise bu testlerden aldığı notların toplamı 70x5=350’dir. Not toplamı 350’den 300’e düştüğüne göre Defne’nin değerlendirme dışı kalan testten aldığı not 50’dir.

Siz de bu şekilde mi çözdünüz problemi yoksa farklı bir yol mu izlediniz?

Problem 2: Komşu iki kenarının uzunlukları 10 ve 8 birim olan bir dikdörtgen ile 6 ve 8 birim olan ikinci bir dikdörtgen düşünelim. Bu dikdörtgenler bir kısımları üst üste gelecek şekilde yerleştiriliyor. Aşağıdaki şekilde örnek bir durum gösterilmiştir. İki dikdörtgende üst üste gelmeyen bölgelerin alanlarının farkı kaçtır?

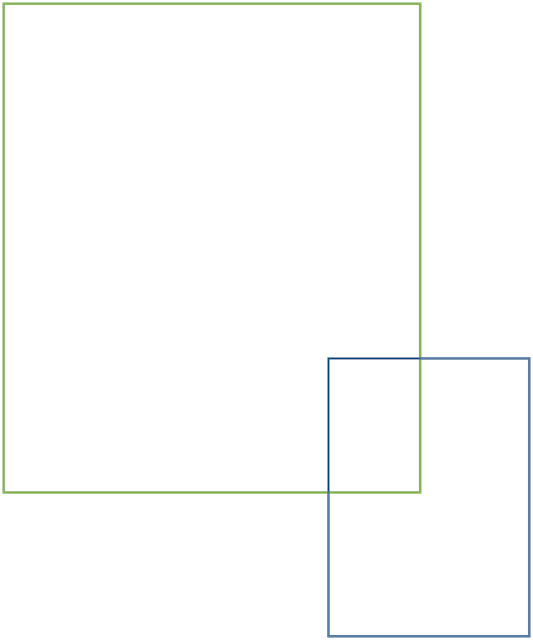
Burada okumaya devam etmeden önce problem üzerinde düşünmenizi rica ediyorum.

İlk bakışta sanki eksik bilgi varmış gibi görünse de bu problemi verilenler ile çözebiliriz. Burada “özel/uç durumları göz önünde bulundurma” stratejisini kullanabiliriz. Soruda bize üst üste gelen kısmın ne kadarlık bir alan olduğuna dair bilgi vermiyor. İki uç durumu düşünelim: İlk durumda dikdörtgenlerimiz sadece bir noktada birbirine değsin. Birinci dörtgenin alanı 10x8=80, ikinci dörtgenin alanı 6x4=24 ve üst üste gelen kısım tek bir nokta olduğuna göre bu kısmın alanı sıfır olacak. O zaman birinci dikdörtgende diğeri ile ortak olmayan alan 80, ikinci dikdörtgende de diğeri ile ortak olmayan alan 24 olacak. Yani bu durumda ortak olmayan alanların farkı 80-24=56 olur.

1. durum        

İkinci uç durumumuz küçük dikdörtgenin tamamen birincinin üzerinde olması. Yani bu kez oluşabilecek en büyük ortak alana bakıyoruz. Bu da küçük dikdörtgenin alanına eşit. O zaman ortak olmayan alanlar birinci dörtgen için 80-24, ikincisi için 0 olacak. Ortak olmayan alanların farkı da yine 56 çıkacak.

Acaba her durumda sonuç iki dikdörtgenin alanlarının farkı mı çıkacak dersiniz?

Şimdi başka bir duruma bakalım. Ortak alan 1 birimkare olsun. O zaman ortak olmayan alanların farkı

(80-1)-(24-1)=56 olur. Sonuç yine aynı çıktı. Aslında ortak alanın büyüklüğü ne olursa olsun, ortak olmayan alanların farkı aynı çıkıyor. Bunun sebebi de iki alandan aynı miktarı çıkarıp sonra fark almamız.

İlk durumda iki alandan da 0 çıkardık, ikinci durumda küçük dörtgeninin alanı olan 24 çıkardık. Bunlar iki uç durumumuzdu. Bu bize çözüm hakkında bir fikir verdi. Ortak alanımız A olursa (80-A)-(24-A)=80-A-24+A=80-24=56 sonucunu elde ederiz. Demek ki ortak alanın büyüklüğü sonucu değiştirmiyor.

2. durum

Peki size bir soru: Eğer bu problemdeki şekil dikdörtgen yerine üçgen veya daire olsaydı çözüm nasıl olurdu?

Bu yazımda matematik problemlerine farklı bir açıdan bakmak, problem çözerken sonuç kadar sürecin de önemli olduğunu vurgulamak istedim. Daha çözülebilecek çok problem, keşfedilebilecek çok şey var. Onları da başka bir zamanda, başka bir yazıda inceleriz.