Matris Nedir? Neden Matrislere İhtiyacımız Var?

Lexashka/iStockphoto.com

Matris Nedir?

Matrisler, satır ve sütunlar hâlinde düzenlenmiş sayı kümeleridir. Bir matrisin satır ve sütunlarını dolduran her sayı veya sembol matrisin elemanıdır.  Matrisin yatay doğrultuda yer alan sırasına satır, dikey doğrultuda yer alan sırasına ise sütun adı verilir. Büyük harf ile isimlendirilen matrislerin boyutu ‘’satır sayısı x sütun sayısı’’ şeklinde belirlenir. Örneğin

 matrisi 2 satırı ve 3 sütunu olan 2 x 3 boyutunda bir matristir. A matrisinin i-inci satırı ve j-inci sütununda yer alan eleman aij simgesiyle gösterilir. Yani yukarıdaki A matrisinin elemanları, a₁₁=5, a₁₂=-1, a₁₃=2 ve a₂₁=0, a₂₂=3 a₂₃=-8’dir.

Satır sayısı sütun sayısına eşit olan matrise kare matris denir. Kare matrislerin sol üst elemandan sağ alt elemana giden doğrultusu esas köşegen veya köşegen olarak adlandırılır. Yani kare matrislerin aii elemanları köşegen elemanlarıdır. Örneğin 

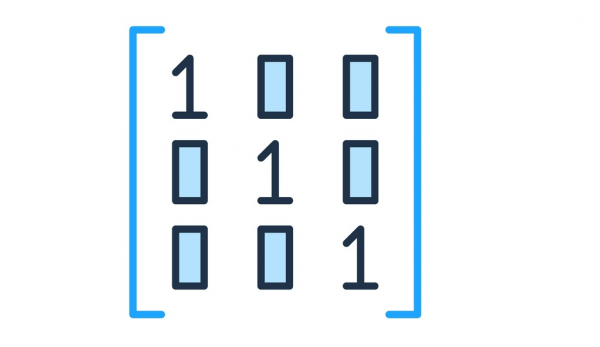
matrisi boyutu 2 x 2 olan bir kare matristir. B matrisinin köşegen elemanları b11=5 ve b22=3’tür. Bir kare matriste asal köşegen üzerindeki tüm elemanlar 1 ve diğer elemanlar 0’lardan oluşuyorsa bu matrise birim matris denir. Aşağıdaki C, D ve E matrisleri farklı boyutlardaki birim matris örnekleridir.

Matrisler arasında toplama çıkarma ve çarpma işlemleri yapılabilir.

Matrislerde Toplama ve Çıkarma İşlemi Nasıl Yapılır?

Aynı boyutlu iki matris toplanabilir veya çıkarılabilir. İki veya daha fazla matriste toplama veya çıkarma işlemi yapılırken satır ve sütun numaraları aynı olan elemanlar birbiriyle toplanır (ya da birbirinden çıkarılır) ve sonuç, toplam matrisin aynı satır ve sütununa yazılır. Örneğin

Matrislerde Çarpma İşlemi Nasıl Yapılır?

Matrislerde çarpma işlemi, iki matrisin çarpımı veya bir matrisin sabit bir sayı ile çarpımı şeklinde olabilir.

• Matrisin Sabit Bir Sayıyla Çarpımı: k ∈ ℝ ve    olmak üzere 

 şeklindedir.

• İki Matrisin Çarpımı: İki matrisin çarpılabilmesi için ise birinci matrisin sütun sayısı, ikinci matrisin satır sayısına eşit olmalıdır. Örneğin 2 x 3 boyutunda bir A matrisi ile 3 x 4 boyutunda bir B matrisi çarpılabilir. Yani A . B matrisi bulunabilir. Çünkü birinci matris yani A matrisinin sütun sayısı, ikinci matris olan B matrisinin satır sayısına eşittir.

Ancak 3 x 4 boyutlu B matrisi ile 2 x 3 boyutlu A matrisi çarpılamaz. Yani
B . A matrisi oluşturulamaz. Çünkü birinci matris olan B matrisinin sütun sayısı, ikinci matris olan A matrisinin satır sayısına eşit değildir. Sonuç olarak matrislerde çarpma işleminin değişme özelliği yoktur.

Matrislere Neden İhtiyacımız Var?

Matrisler 19. yüzyılda İngiliz matematikçi Arthur Cayley tarafından cebirsel işlemlerde kullanılmak üzere geliştirildi. Örneğin 5x - 3y = -1 ve -2x + y = -2 denklemlerinin çözümleri olan x = 7 ve y = 12 değerleri, matrisler yardımıyla bulunabilir. Bunun için öncelikle iki bilinmeyenli iki denklem aşağıdaki gibi bir sistem olarak yazılır.

Daha sonra bu denklem sisteminin çözümüne ters matris metodu, Cramer yöntemi ve Gauss Eliminasyon yöntemi gibi pek çok yöntemle ulaşılabilir.

Universal History Archive / Contributor/ gettyimages.com

İngiliz matematikçi Arthur Cayley

Matrislerin matematik yanı sıra fizik, ekonomi, istatistik ve mühendislik bilimlerinde pek çok uygulama alanı vardır. Örneğin ekonomi ve istatistik alanlarında kullanılan analizlerde matrisler yer alır. Ayrıca bir bilgisayar oyununun tasarlanabilmesi için öncelikle matris kavramının bilinmesi gerekir. Çünkü tüm üç boyutlu programlamalarda veriler, matrisler şeklinde tutulur. Pyton, C ve Matlab gibi programlama dillerinde matrisler kullanılır. Matrisler ayrıca bankalar gibi şifrelemenin kullanıldığı veya veri güvenliğinin sağlandığı her uygulamada yer alır. Bunun için veriler bir matris ile çarpılarak gizlenir. Kullanılacak matrisin boyutunun büyüklüğü şifrelemenin güvenlik düzeyini artırır.

Kaynaklar :

• https://seattle.aie.edu/articles/video-game-math-matrices/
• https://math.libretexts.org/Bookshelves/Applied_Mathematics/Applied_Finite_Mathematics_(Sekhon_and_Bloom)/02%3A_Matrices/2.05%3A_Application_of_Matrices_in_Cryptography
• https://math.mit.edu/~gs/linearalgebra/ila6/ila5cryptography.pdf
• https://news.mit.edu/2013/explained-matrices-1206