Fibonacci Dizisinden Altın Orana
Fibonacci dizisi bir sayı dizisidir ve {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …} şeklinde devam eden sonsuz sayılardan oluşur.

Fibonacci dizisi bir sayı dizisidir ve {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …} şeklinde devam eden sonsuz sayılardan oluşur. Dizi, İtalyan matematikçi Leonardo Fibonacci’nin 1202 yılında yazdığı Liber Abaci (Hesap Kitabı) adlı kitabındaki bir problemin cevabıdır. Kitaptaki problem ise şöyle: Belirli bir bölgeye yeni doğmuş bir tavşan çifti (bir dişi, bir erkek) konuluyor. Her tavşan çifti ikinci aydan itibaren yetişkin hâle geliyor ve her ay yeni bir tavşan çifti (bir dişi, bir erkek) doğuruyor. Tavşanların hiç ölmediği varsayılırsa bu bölgede bir yıl sonra kaç çift tavşan olur?
Problemin çözümünde her ay için sırasıyla 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 sayıları elde edilir.
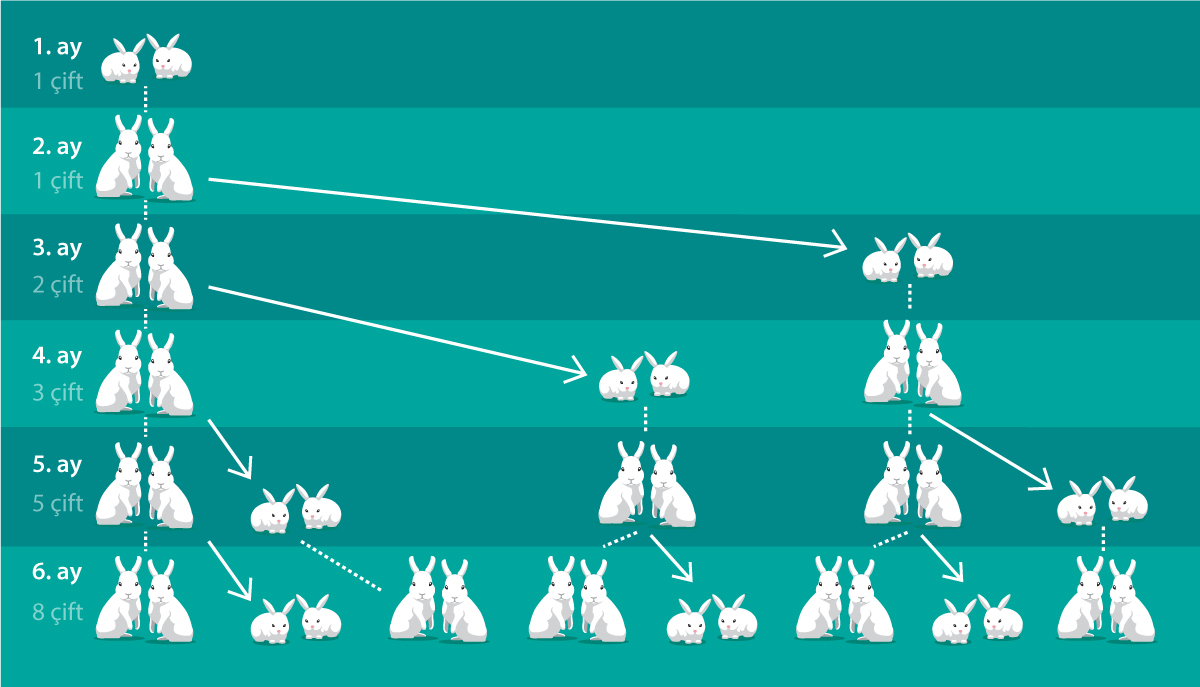
Peki, 100 ayın sonunda bölgede kaç tavşan çifti olur?
İşte bunu hesaplamak biraz zordur. Çünkü dizinin üçüncü teriminden itibaren, her terim kendisinden önceki ardışık iki terimin toplamıyla bulunur. Bu durum, 100. terimin değeri için kendisinden önceki 99 terimin de bulunmasını gerektirir.
Fibonacci dizisi matematiksel olarak şu şekilde gösterilir:
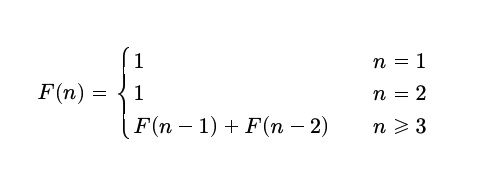
Buradaki F(n), n. terimi belirtir. Yani, Fibonacci dizisinin üçüncü ve sonsuz sayıdaki diğer terimleri F(1)=1=F(2) başlangıç değerleriyle ve F(n)=F(n-1)+F(n-2) eşitliği ile üretilir. Burada olduğu gibi, herhangi bir dizinin tüm terimlerinin (başlangıç değerleri hariç) kendisinden önceki terimlerle bulunmasını sağlayan eşitliğe “yineleme bağıntısı” denir.
Fibonacci dizisi bazı ilginç özellikler sahiptir. Örneğin;
- Dizinin üç ve üçün katlarındaki terimleri 2’ye, dört ve dördün katlarındaki terimleri 3’e, beş ve beşin katlarındaki terimleri 5’e bölünür.
- Dizinin herhangi ardışık on teriminin toplamı her zaman 11’in katıdır.
- Dizinin ikinci teriminden sonraki her ardışık iki terimi aralarında asaldır.
- Dizinin herhangi ardışık iki teriminin kareleri toplamı yine bu dizinin bir terimidir.
Dizi ne kadar detaylı incelenirse o kadar büyüleyici ve merak uyandırıcı olduğu görülür. Çünkü dizinin sayıları arasında bunlardan farklı daha birçok ilginç ilişki var. Bu ilişkileri kendiniz araştırarak veya gözlemleyerek bulabilirsiniz.
Her ne kadar tavşanların doğada çoğalma problemi gerçekçi olmasa da dizinin terimlerine doğada sıkça rastlanması ve dizinin ardışık iki teriminden büyük terimin küçük terime oranının giderek “altın oran”a yaklaşması Fibonacci dizisini popüler hâle getirmiştir. Örneğin, dizinin terimleri çiçeklerin taç yapraklarında görülebilir.

Ayrıca çam kozalağı ve ayçiçeği tohumlarında merkezden dışa doğru sağdan sola veya soldan sağa çizilen sarmal sayılar da dizinin terimlerindendir.
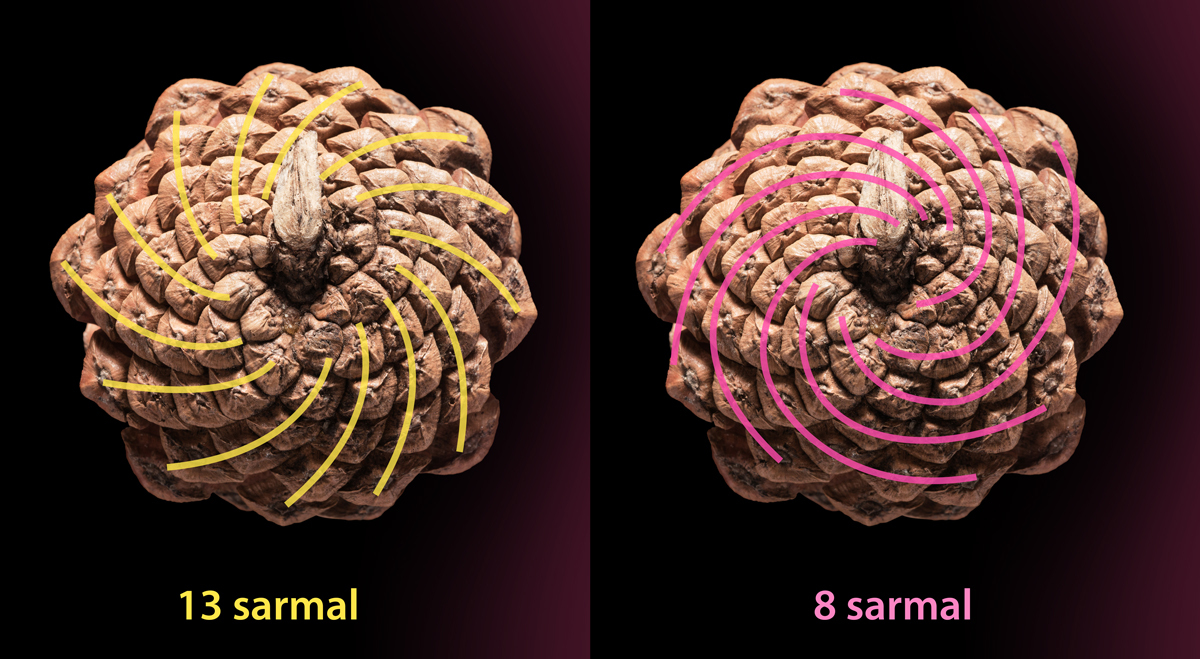
Dizinin ardışık terimleri arasındaki oranlara bakıldığında ise bu oranların 1,618 sayısına yaklaştığı görülür. Aynı sayı herhangi bir AB doğru parçası üzerindeki bir C noktası için, tüm parçanın büyük parçaya oranı ile büyük parçanın küçük parçaya oranının birbirine eşitlenmesiyle bulunur. Bu sayıya “altın oran” denir ve “Φ” (Fi) sembolü ile gösterilir.
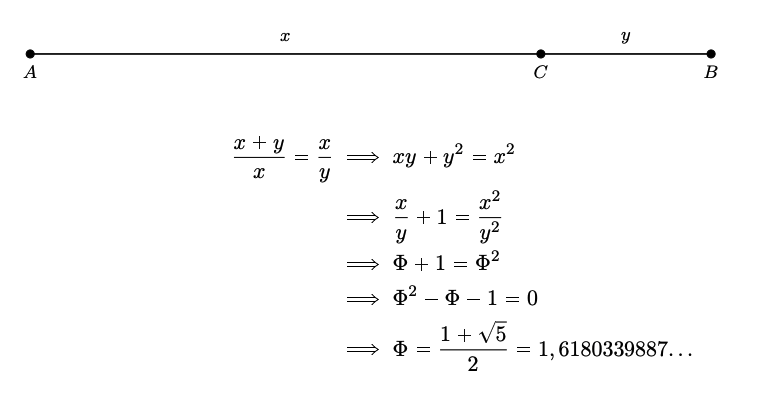
“Altın dikdörtgen” ise kenar uzunlukları AB doğru parçası ve AC doğru parçasıyla orantılı olan dikdörtgendir. Altın dikdörtgen içerisinde bulunan ve kenar uzunlukları Fibonacci dizisinin terimlerinden oluşan kareler sırasıyla çıkarıldığında geriye kalan her bir dikdörtgen yine altın dikdörtgen olur.
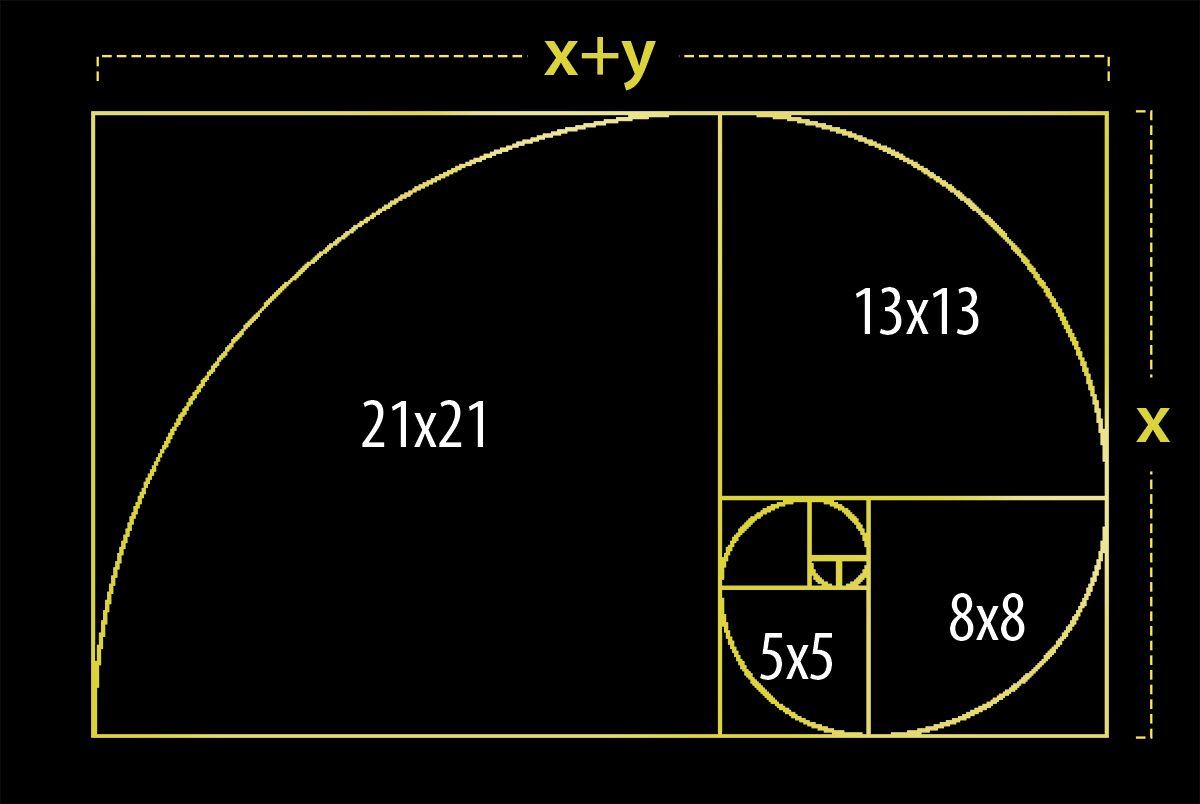
Altın dikdörtgen içerisinde bulunan sarmal ise “altın sarmal” olarak isimlendirilir.
Altın dikdörtgen ve altın oran birçok mimari ve sanat eserinde kullanılıyor. Leonardo da Vinci’nin Mona Lisa ve Son Akşam Yemeği isimli tabloları, Yunanistan’daki Parthenon Tapınağı ve Mısır’daki piramitler, Mimar Sinan tarafından inşa edilen Süleymaniye ve Selimiye camileri de altın oranın kullanıldığı eserlerden bazılarıdır. Örneğin Mona Lisa tablosundaki altın sarmal Mona Lisa’nın burnunun ucundan dönerek çenesinin altını sıyırır ve sol kolunun dirseğinden başparmağına kadar uzanır.

Kasırga gibi atmosfer olayları, salyangoz ve bazı kabuklu deniz canlılarında ise altın sarmal görülür.

Ayrıca, piyano, keman gibi müzik aletleriyle Beethoven ve Mozart gibi ünlü bestecilerin eserlerinde de altın orana rastlanır. Örneğin piyano klavyesinde bir oktav, biri diğerinden daha yüksek olan iki nota arasındaki müziksel aralığı temsil eder. Bir oktav, 5 siyah ve 8 beyaz tuş olmak üzere toplam 13 tuştan oluşur. Bu sayılar birer Fibonacci sayısıdır.

Altın oran hemen hemen tüm medeniyetler tarafından kullanılan en eski denge sistemlerinden biridir. Altın oran kullanılarak yapılan her eser estetik açıdan güzel görünür. Öyle ki bu oran kullanılarak yapılan tüm eserler döneminin en ünlü eserleri olmuştur.
Kaynak:

















