Paradoksal Durumlar
Paradoks kelimesini daha önce hiç duymuş muydunuz? Bu yazımızda paradoks olarak adlandırılan bazı tuhaf durumlardan bahsedeceğiz.
Paradoks kelimesini daha önce hiç duymuş muydunuz? Bu yazımızda paradoks olarak adlandırılan bazı tuhaf durumlardan bahsedeceğiz.
Hemen birkaç örnek verelim:
Bir kasabada sadece bir erkek berberi var ve bu berber de erkek. Berber kasabadaki erkeklerden sadece kendini tıraş etmeyen kişileri tıraş ediyor. Bu durumda berberi kim tıraş eder?
“Bu cümle yanlıştır.” cümlesi sizce doğru mudur, yanlış mıdır?
“Ben her zaman yalan söylerim.” diyen bir kişi sizce doğru mu söylüyor yoksa iddia ettiği gibi yalan mı söylüyor?
Rivayete göre Antik Yunan düşünürü Socrates demiş ki: “Bildiğim tek şey, hiçbir şey bilmediğimdir.” Koskoca düşünür böyle dediyse bir bildiği vardır, değil mi?
Bu örneklerden de anlaşılabileceği gibi kendisiyle veya birbiriyle çelişen ifadeler, hem doğru hem de yanlışmış gibi görünen durumlar paradoks olarak adlandırılıyor.
Paradoks, Yunanca kökenli bir kelime. Para (dışında, ötesinde) eki ile dokein (düşünmek) kelimesi birleştirilerek paradoxos sıfatı türetilmiş. Bu sıfat ise “beklenti ile çelişen” anlamına geliyor. Türk Dil Kurumu sözlüğüne göre kelime “aykırı düşünce; çelişki; düşünceler arasında tartışmaya açık, kesin bir yargı içermeyen karşıtlık” anlamlarında kullanılıyor.
Şimdi biraz Antik Yunan filozoflarının ortaya attığı paradokslara bakalım.
Protagoras Paradoksu
Ünlü filozof Protagoras’tan hukuk dersi almak isteyen bir genç vardır. Ne yazık ki bu gencin Protagoras’a ödeme yapacak gücü yoktur. Şöyle bir anlaşma yaparlar. Protagoras eğitim için ücret almayacak, genç de eğitimi bittikten sonra ilk kazandığı davanın parasını Protagoras’a verecektir. Fakat eğitim bittikten sonra genç avukat bir süre hiç dava almaz, Protagoras da ücretinin ödenmesi için gence dava açar. Genç de avukat olduğu için davada kendini savunur. Yani bu dava gencin ilk davasıdır. Gencin savunması şu şekildedir: “Bu davayı ya kazanacağım ya da kaybedeceğim. Eğer kazanırsam para ödemek zorunda kalmayacağım. Eğer kaybedersem bu avukat olarak ilk davam olduğu için henüz bir dava kazanmamış olacağım ve yine para ödemeyeceğim.” Bunun üzerine Protagoras da şu şekilde cevap verir: “Tamamen yanılıyor, eğer ben kazanırsam o bana parayı ödemek zorunda çünkü dava bununla ilgili. Eğer kaybedersem, bu kazandığı ilk dava olacak ve yine bana paramı ödemek zorunda kalacak.” Böyle bir davada hâkim olmak ister miydiniz?
Zeno’nun Paradoksları
Şimdi, Antik Yunan düşünürlerinden Zeno’nun paradokslarından iki tanesini inceleyeceğiz. Bu paradokslar diğerlerinden biraz farklı. Çünkü sonsuzluk kavramı ile ilgililer.
İlk inceleyeceğimiz paradoksta olay Yunan mitolojisinin kahramanlarından Aşil ile bir kaplumbağa arasında geçiyor. Aşil ile kaplumbağa yarış yapacaklar. Aşil iyi bir koşucu olduğu için kaplumbağanın yarışa kendisinden 100 metre ileride bir noktada başlamasına izin veriyor. Her ikisinin de sabit hızla ilerlediğini varsayıyoruz. Aşil 100 metre ilerleyip kaplumbağanın yarışa başladığı noktaya geldiğinde, kaplumbağa da bir metre ilerlemiş oluyor. Bu durumda ilk 100 metrede Aşil kaplumbağayı yakalayamıyor. Aşil 1 metre daha gittiğinde kaplumbağa da biraz daha ilerlemiş oluyor. Aşil yine yakalayamıyor kaplumbağayı. Aralarındaki uzaklık gittikçe azalsa bile kaplumbağa her seferinde bir miktar ilerleyeceği için Zeno bu şekilde devam eden yarışta Aşil’in kaplumbağayı asla yakalayamayacağını iddia ediyor.
Zeno’nun ikinci paradoksu da şu şekilde: A noktasından B noktasına gitmek isteyen kişinin önce aradaki uzaklığın yarısını katetmesi gerekir. Orta noktaya C diyelim.
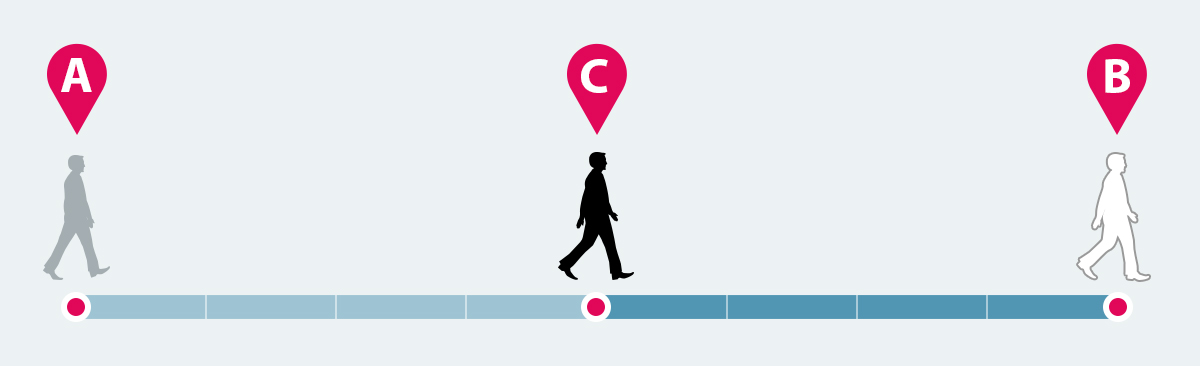
C noktasından B’ye gitmek için de önce aradaki uzaklığın yarısını katetmesi gerekir. C ile B’nin orta noktası D olsun.
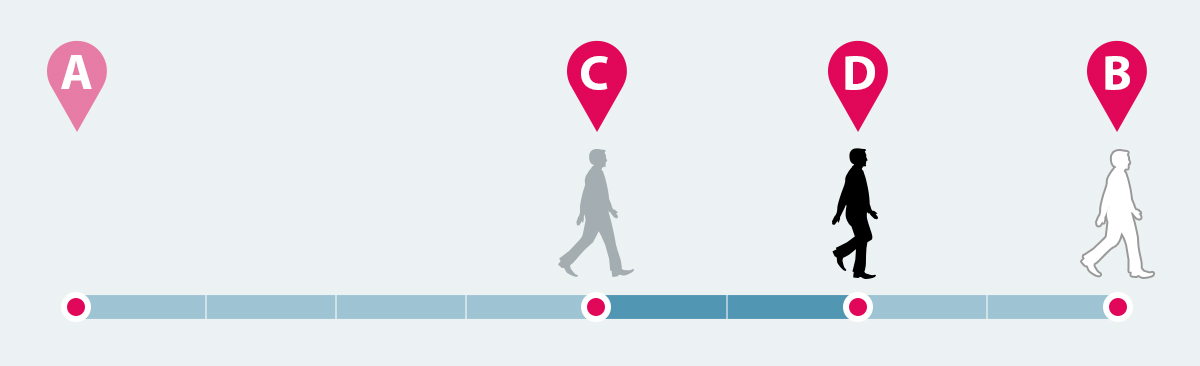
D’den B’ye gitmek için de öncelikle D ile B arasındaki uzaklığın yarısını katetmesi gerekir.
Zeno bu şekilde devam edildiğinde bu kişinin B noktasına hiç varamayacağını iddia ediyor çünkü her seferinde önünde katetmesi gereken bir mesafe var.
Aşil’in kaplumbağayı yakalayıp geçebileceğini, bir kişinin bir yerden başka bir yere gidebileceğini bildiğimize göre bu iddialar doğru olamaz, değil mi? Peki, hata nerede?
Matematikçiler bu paradoksları sonsuz toplamın sonlu bir sayıya eşit olduğunu göstererek çözmüşler. Örneğin ikinci paradoksta A ile B noktaları arasındaki uzaklığa 1 birim dersek, matematikçiler gidilecek yolun yani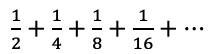 
sonsuz toplamının 1’e eşit olduğunu bulmuşlar. Sonsuz bir toplamın bir sayıya eşit olabileceği analiz yöntemleri ile gösterilebilir. (Yalnız dikkat: Her sonsuz toplam bir sayıya eşit değildir.)
Şimdi bir örnek üzerinde daha duralım. x ve y 0’dan farklı iki doğal sayı olsun. Bu sayılardan birinin diğerinin iki katı olduğu biliniyor. Şimdi size iki iddia sunuyoruz.
İddia 1: Eğer x sayısı y sayısından büyükse x’ten y’yi çıkararak elde edeceğimiz sayı, eğer y sayısı x sayısından büyükse y’den x’i çıkararak elde edeceğimiz sayıdan büyüktür.
İddia 2: Eğer x sayısı y sayısından büyükse, x’ten y’yi çıkararak elde edeceğimiz sayı ile eğer y sayısı x sayısından büyükse, y’den x’i çıkararak elde edeceğimiz sayı eşittir.
Kısacası büyük sayıdan küçüğü çıkarıyoruz. Birinci iddia, büyük sayının x olduğu durumda elde edeceğimiz farkın büyük sayının y olduğu durumda elde edeceğimiz farktan büyük olacağını söylüyor. İkinci iddia ise bu farkların eşit olacağını söylüyor.
Siz “Hangisi doğru acaba?” diye düşünürken biri çıkıp iki iddianın da doğru olduğunu söyleyerek aşağıdaki kanıtları sunuyor.
Bu iki iddianın doğru olması matematikte bir çelişki yaratır çünkü ilk iddia “Bir sayı diğerinden büyüktür.” diyor, ikinci iddia “Bu sayılar eşittir.” diyor. Bildiğimiz matematikte ikisi birden doğru olamaz! Merak etmeyin, matematikte yeni bir çelişki bulmadık, başta paradoks gibi görünen bu durumun aslında çok basit bir açıklaması var: ilk iddia yanlış. O zaman kanıtta bir hata var. Bu kanıtı ortaya atan kişi sizce nerede hata yapmış? (İpucu: Elimizdeki sayılar 3 ve 6 olsun. Bu sayıları kullanarak ispat adımlarını takip edin.)
Yazının başında bahsettiğimiz berber paradoksu da matematikte ortaya çıkan bir çelişki ile bağlantılı. Bu çelişki Russel paradoksu olarak bilinir. Berber paradoksunu da Russel’ın bulduğu çelişkiyi açıklamak için kullandığı söylenir. 1900’lü yılların başında Alman matematikçi Frege’nin ortaya koyduğu kümeler kuramında bir çelişki bulan Russel bunu bir mektupla kendisine bildirir. Bu paradoks bir kümenin kendisini eleman olarak içerip içeremeyeceği ile ilgilidir. Bu çelişki başta bir kriz yaratmışsa da daha sonra giderilerek kümeler kuramı sağlam temellere oturtulmuştur.
Çok daha eski dönemlerde, Antik Yunan’da ortaya çıkan bir paradoks da ortalığı karıştırmıştı. Bazı kaynaklara göre “matematik tarihindeki ilk büyük kriz”e yol açan bu paradoksun, kenar uzunluğu 1 birim olan bir karenin köşegen uzunluğunun bulunması sırasında ortaya çıktığını biliyor muydunuz? Nasıl mı? Onu da sonra anlatırız.
Kaynaklar:
- Nesin, A., Matematik ve Gerçek, Nesin Yayıncılık, İstanbul, 2012.
- Smullyan, R. M., The Gödelian Puzzle Book: Puzzles, paradoxes and proofs, Dover Publications, NY, 2013.
- https://www.merriam-webster.com/dictionary/paradox
- https://sozluk.gov.tr/
