Şifrelemenin Temeli Asal Sayılar
2, 3, 5, 7, 11, … şeklinde devam eden, kendisinden ve 1’den başka pozitif böleni olmayan 2 ve 2’den büyük sayılara asal sayı dendiğini birçoğumuz biliyoruz. Peki, asal sayılar neden önemlidir? Günlük hayatta ne işimize yarar?
Robert Brook/Science Photo Library/Getty Images
1’den büyük her tam sayı ya asal bir sayıdır ya da asal sayıların çarpımlarından oluşur. Örneğin 11 asal bir sayı iken, 12 sayısı 12=22.3 şeklinde asal sayıların çarpımı sonucu elde edilir. Yani 1’den büyük her tam sayı aslında asal sayılar ile üretilir. Bu da onların, sayıların birbiriyle ilişkisini açıklayan sayı teorisi bilim dalının merkezinde olmasını sağlar.
Asal sayılar ayrıca şifrelemenin de temelini oluşturur. Günümüzde e-posta ve diğer dijital işlemlerin veri şifrelemesinde yaygın olarak kullanılan RSA şifreleme yönteminde, veriler asal sayılardan yararlanılarak şifrelenir. Böylece istenmeyen kişilerin verilere ulaşması engellenir. İki büyük asal sayı çarpımının şifreleme anahtarı olarak kullanıldığı bu yöntemde, seçilen asal sayılar gizli kalır ve sadece bu anahtarın çarpanları olan asal sayıları bilen kişi şifreyi çözebilir. Büyük sayıları asal çarpanlarına ayırmak zor bir işlem olduğu için RSA şifreleme yönteminde olabildiğince büyük asal sayılar kullanılır ve böylece şifrelemenin güvenliği artırılır.
Petri Oeschger/Moment/Getty Images
Peki belirli sayılar arasındaki asal sayıları nasıl bulabiliriz?
1 ile 100 arasında bulunan 25 adet asal sayıyı (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97) kolayca yazabiliriz. Ama daha büyük asal sayıları listelemek, örneğin 1 ile 100.000.000 arasındaki asal sayıları belirlemek kolay değildir. Çünkü asal sayılar arasında düzenli bir örüntü bulunmadığı için tüm asal sayıları üretebileceğimiz bir formül yazılamıyor. İlk 25 asal sayıya baktığımızda, sayılar arasında düzenli bir örüntü olmadığı görülebilir. Asal sayıların listesini oluşturmak için her bir pozitif tam sayıyı tek tek değerlendirerek asal olup olmadığına karar vermeliyiz. Ancak büyük sayıları göz önünde bulundurduğumuzda, bu yöntem ile asal sayı listesi oluşturmak epey zamanımızı alacaktır.
Elimizde tüm asal sayıları kolayca üreten bir formül olmasa da 1 ile belirli bir n sayısı arasında (n sayısı dâhil) ne kadar asal sayı bulunduğunu yaklaşık olarak hesaplayan bir formülümüz var: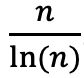 
. Formüldeki 
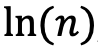, n’nin doğal logaritmasıdır ve hemen hemen tüm hesap makinelerinde bulunur. Verilen aralıkta bulunan asal sayıların gerçek değeri ise asal sayı sayma fonksiyonu olan 
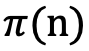ile gösterilir.
Lamberto Jesus/iStock.com
Örneğin 1 ile 1.000 arasında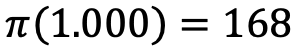 
adet asal sayı vardır. Formül ise bize yaklaşık olarak 
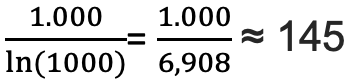sayısını verir. Bu hesaplamanın doğruluk oranı %86 civarındadır. Formülü kullanarak 1 ile 100.000 arasında ne kadar asal sayı bulunduğuyla ilgili bir hesap yaptığımızda ise doğruluk oranı %90’a çıkar. Gerçekte bu sayılar arasında tam olarak 9.592 adet 
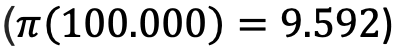asal sayı bulunurken formül yaklaşık olarak 8.686 
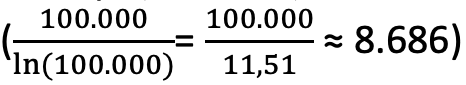sayısını verir.
n sayısı yeterince büyük seçildiği zaman ise formülün hesapladığı aralıkta bulunan asal sayı adedi ile gerçekte bulunan asal sayı adedinin oranı neredeyse 1’e eşit olur. Yani formülün doğruluk oranı %100’e ulaşır. Bu sonuç asal sayı teoremi olarak bilinir.
Şifrelemede önemli bir yeri olan asal sayıların tam sayılar arasında hangi kurala göre dağıldığını bilmesek de tam sayılar arasındaki adedini yaklaşık olarak hesaplayabiliyoruz.
Kaynak:
- http://math.uchicago.edu/~may/REU2012/REUPapers/LiuR.pdf
