Hilbert’in Sonsuz Otel Paradoksu
Sonsuz sayıda odasının tümü dolu olan bir otel düşünelim. Resepsiyona gelen yeni bir müşteriye bu otelde nasıl yer bulabilirsiniz? Peki, sonsuz sayıda yolcusu olan bir otobüsteki kişiler bu otelde konaklayabilir mi?

Çizim: Umut Aybek
Hilbert’in otelinde sonsuz sayıda oda vardır ve bu odalar 1, 2, 3, … şeklinde pozitif tam sayılarla numaralandırılır. Tüm odaların dolu olduğu bir hafta sonu otele rezervasyonu olmayan bir müşteri gelir ve bir oda ister. Resepsiyon görevlisi, bu müşteriyi geri çevirmek istemez ve ona bir oda bulmaya karar verir. Nasıl mı?
Öncelikle Hilbert’in otelinde hiçbir zaman boş oda bulunmaz ancak yeni müşteriler için her zaman yer bulunabilir. Bu çelişkili durum sonsuzluk kavramıyla ilgilidir. Alman matematikçi David Hilbert’in bu düşünce deneyi, bizlere imkânsız gibi görünen sonuçlara nasıl ulaşılabildiğini sonsuzluk kavramının incelikleriyle gösteriyor.
Gelelim şimdi yukarıdaki sorunun cevabına.
Görevli 1. odada kalan kişinin 2. odaya, 2. odadakinin 3. odaya, 3. odadakinin ise 4. odaya taşınmasını ister. Bu şekilde devam edildiğinde n. odadaki kişi, n+1. odaya geçmiş olur. Böylece 1 numaralı oda boşalır ve görevli yeni gelen müşteriye bu odayı verebilir. Hilbert’in otelinde sonsuz sayıda oda olduğu için her yeni gelen müşteriye bu şekilde bir yer bulunabilir. Aslında burada mevcut oda numaralarından oluşan küme ile yeni oda numaralarından oluşan küme arasında aşağıdaki gibi birebir eşleme yapılır.
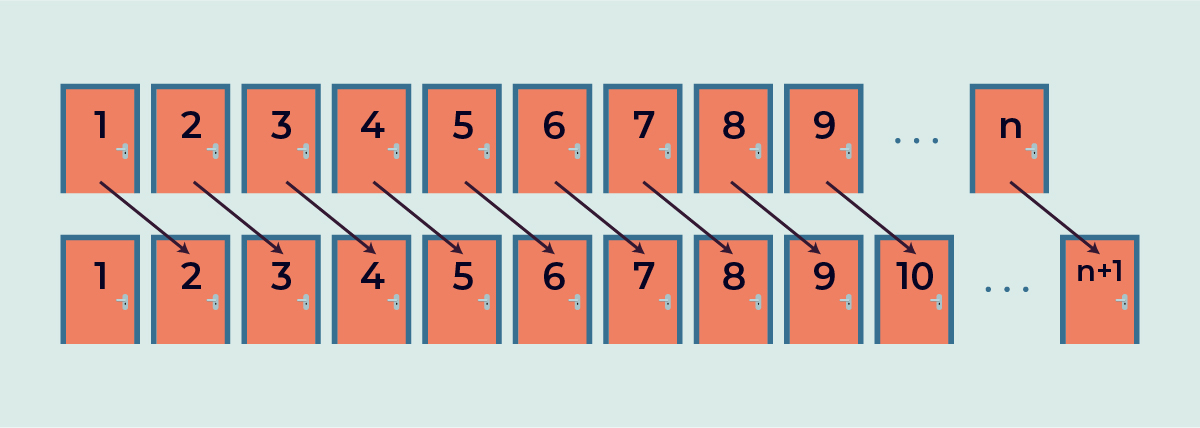
Çizim: Umut Aybek
Fakat oda sayısı sınırlı olan herhangi bir otelde -otelin ne kadar çok odası olursa olsun- bu yöntemin işe yaramayacağını hepimiz biliyoruz. Çünkü sınırlı bir otelde en büyük numaralı odada kalan kişinin taşınabileceği yeni bir oda bulunmaz.
Peki, bu otele “Sonsuzluk Turizm” isimli sonsuz sayıda yolcusu olan bir otobüs gelirse bu otobüsteki kişilere otelde yer bulunabilir mi?
Evet, otel dolu olmasına rağmen bu otobüsteki kişilere de otelde yer bulunabilir ama yukarıdaki yöntemle değil. Çünkü 1. odadaki kişi yüz milyon sonraki odaya ve diğer odadakiler daha sonraki odalara taşınsa bile sadece bu yüz milyon kişiye oda bulunur. Fakat geriye hâlâ yerleşmeyi bekleyen sonsuz sayıda insan kalır. Bu durumda görevli sonsuz sayıda kişiye oda bulmak için başka bir yöntem uygulamalıdır. Sizce bu yöntem nasıl olmalı?
Eğer yeteri kadar düşündüyseniz resepsiyon görevlisinin izleyeceği yeni yöntemi inceleyelim.
Görevli 1. odada kalan kişinin 2. odaya, 2. odadakinin 4. odaya, 3. odadakinin ise 6. odaya taşınmasını ister. Bu şekilde devam edildiğinde n. odadaki kişi, 2n. odaya geçmiş olur. Yani pozitif tam sayılar kümesi ile pozitif çift tam sayılar kümesi arasında birebir eşleme yapılır. Böylece oteldeki tüm kişiler çift numaralı yeni odalara taşınır ve tek numaralı odalar boş kalır. Şimdi otele yeni gelen otobüsteki yolcular, boş olan tek numaralı odalara 1. koltuktaki kişi 1. odaya, 2. koltuktaki kişi 3. odaya, 3. koltuktaki kişi 5. odaya olacak şekilde yerleşebilir. Yani bu otobüste n. koltukta oturan kişi, 2n-1 numaralı odaya yerleşir. Böylece otobüsteki tüm kişiler otelde kalabilir.
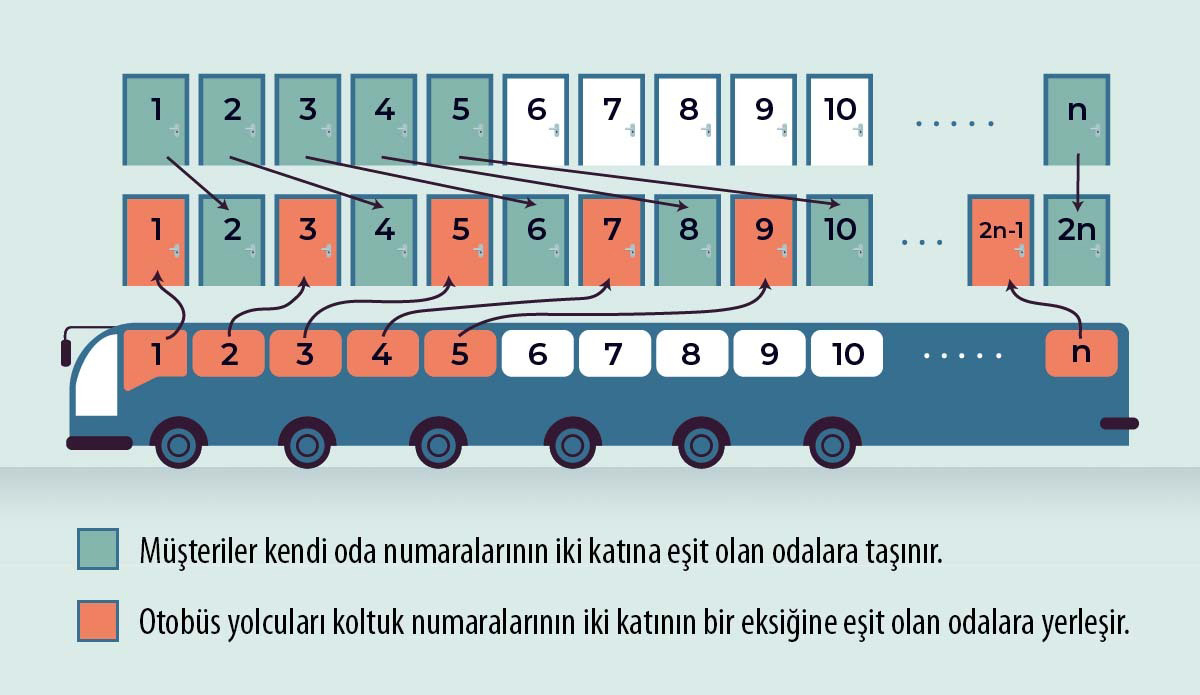
Çizim: Umut Aybek
Şimdi tüm odaları dolu olan Hilbert’in oteline sonsuz sayıda yolcu taşıyan “Sonsuzluk Turizm” isimli otobüslerden sonsuz tane geldiğini düşünelim ve tüm yolculara konaklayabilecekleri bir odayı nasıl bulabileceğimizi öğrenelim.
Aslında bir önceki sorunun sadece bir adım ötesinde olan bu problem, asal sayıların sonsuzluğu ile çözülür. (Asalların neden sonsuz sayıda olduğunu merak ediyorsanız önceki yazımızdan öğrenebilirsiniz.)
Bu problemin çözümüne, daha önce olduğu gibi, oteldeki tüm müşterilerden kaldıkları oda numaralarının iki katına eşit olan odaya taşınmaları istenerek başlanır. Böylece yeniden tek numaralı odalar boş kalır. Yeni gelen otobüslerden biri koltuk sırasına göre ilk tek asal sayı olan 3 ve 3’ün kuvvetlerine eşit odalara yerleşir. Yani otobüsün 1. koltuğundaki kişi 3 numaralı odaya, 2. koltuğundaki kişi 9. odaya (32=9), 3. koltuğundaki kişi 27. odaya (33=27) ve bu şekilde n. koltuktaki kişi 3n numaralı odaya yerleşir. Yeni gelen diğer bir otobüsün yolcuları ise koltuk sırasına göre 5 ve 5’in kuvvetlerine eşit odalara yerleşir. Yani otobüsün 1. koltuğundaki kişi 5. odaya, 2. koltuğundaki kişi 25. odaya (52=25), 3. koltuğundaki kişi 125. odaya (53=125) ve n. koltuğundaki kişi 5n. odaya yerleşir. Sırasıyla diğer otobüslerdeki yolcular 7, 11, 13, .. şeklinde sonsuz sayıda olan asal sayıların kuvvetlerine eşit odalara yerleşebilir. Böylece bu son zorlu problem de çözülmüş olur.
Peki asal sayıların kuvvetlerine eşit oda numaralarının her zaman boş olacağını nasıl biliyoruz? İşte bu sorunun cevabı aritmetiğin temel teoreminde gizli. Çünkü pozitif her tam sayı, asal sayıların çarpımı şeklinde benzersiz olarak yani tek bir şekilde yazılabilir. Bu durumda herhangi bir oda numarası bir asal sayının kuvveti ise başka bir asal sayının kuvvetine eşit olamaz. Ayrıca tek asal sayıların hiçbir kuvveti ikiye bölünemez ve bu odalar boş olduğu için yeni bir misafir kabul edebilir.
Son olarak bütün yerleştirmeler tamamlandığında ikinin katı ve herhangi bir asal sayının kuvvetine eşit olmayan sonsuz sayıda odanın boş kaldığını fark etmişsinizdir. Örneğin 1, 15, 21, 33, 35, 39, 45, … numaralı odalar gibi. Yani, son anda gelen her yeni müşteri de bu otelde konaklayabilir.
Kaynaklar: