Bazı sayıların mutlu bazı sayıların mutsuz bazı sayıların ise narsistik sayı olarak isimlendirildiğini biliyor muydunuz? Örneğin 1 sayısı mutlu bir sayı iken 4 sayısı mutsuz bir sayı. Ancak hem 1 hem de 4 sayıları narsistik sayılar arasında. Peki bu sayılar neden böyle adlandırılıyor? Gelin hep birlikte öğrenelim.

“2 ile toplandığında 1’i  veren sayı nedir?” sorusunun cevabı ile 2+x=1 denkleminin çözüm kümesi aynıdır. Bu denklemin çözümü için ihtiyaç duyduğumuz sayı ise negatif bir sayıdır. Peki negatif sayıların matematikteki önemi nedir?

Sayılar teorisinde belirli özelliklere göre bir araya getirilerek oluşturulan sayı kümeleri vardır: pozitif tam sayılar, asal sayılar, mükemmel sayılar, üçgensel sayılar gibi. Bunların yanı sıra “arkadaş sayılar” veya “dost sayılar” olarak bilinen bir sayı kümesi de vardır. Gelin bu kümenin hangi sayılardan oluştuğunu birlikte öğrenelim.

Sayıları düşündüğümüzde, bazı sayıların diğerlerinden farklı özellikte olduğunu kolayca görebiliriz. Örneğin 10 sayısı 1, 2 ve 5 sayıları ile bölünebilirken, 11 sayısı sadece 1 ve 11 yani kendisi ile bölünebilir. Pozitif tam sayılar kümesinde bu şekilde kendisinden ve 1’den başka böleni olmayan, 2 ve 2’den büyük birçok sayı vardır. Bu sayılara “asal sayı” denir. 

Matematikte zaman zaman beklenmedik bir şekilde ortaya çıkan güzel diziler vardır. Bunlardan biri de 1951 yılında Alfred Moessner tarafından keşfedilen, pozitif tam sayıların kuvvetlerinin üretilmesi yöntemidir. Bu yöntem matematikte ‘’Moessner mucizesi’’ olarak bilinir.

Sonsuz sayıda odasının tümü dolu olan bir otel düşünelim. Resepsiyona gelen yeni bir müşteriye bu otelde nasıl yer bulabilirsiniz? Peki, sonsuz sayıda yolcusu olan bir otobüsteki kişiler bu otelde konaklayabilir mi?

Binbir Gece Masalları’ndaki “1001” sayısında olduğu gibi, soldan sağa veya sağdan sola yazıldığında aynı olan başka sayılar aklınıza geliyor mu? Peki, palindrom sayı olarak isimlendirilen bu sayıların ilginç özelliklerini öğrenmek ister misiniz?

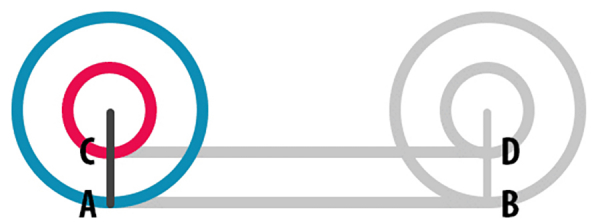
Farklı yarıçaplara sahip, ortak merkezli iki dairesel tekerlek düşünelim. Bu tekerlekleri kaydırmadan bir tam tur döndürdüğümüzde, tekerleklerin aldığı mesafelerin birbirine eşit olması imkânsız görünüyor değil mi? Peki, bu kafa karıştırıcı durum nasıl açıklanabilir?

Yarılama yöntemi aslında bir kök bulma metodudur. Sürekli bir fonksiyonun kökünü bulmak için kullanılır. Kökün bulunduğu aralık art arda ikiye bölünerek yani yarılanarak daraltılır ve bu şekilde sürekli daralan aralığın uç noktaları köke doğru yaklaşır. Kökün içerisinde bulunduğu aralık istenilen derecede küçük olana kadar yöntem yinelenir.

“Peki ama şimdi hangi fonksiyonun kökünü bulacağız? Bizim elimizde sürekli bir fonksiyon yok ki, sadece karekök iki sayısı var.” diye düşünebilirsiniz. 

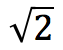 sayısı aslında ikinci dereceden f(x)=x²-2  fonksiyonunun bir köküdür. 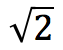sayısının 1 ile 2 sayıları arasında bir değere sahip olduğunu biliyoruz. Yani 1< 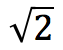< 2’dir. Gelin şimdi hep birlikte  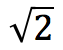sayısının yaklaşık değerini yüzde birler basamağına kadar hesaplayalım.

Bu videoda bilinen ilk irrasyonel sayı olan 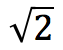 sayısının yaklaşık değerini yarılama yöntemiyle hesaplıyoruz.

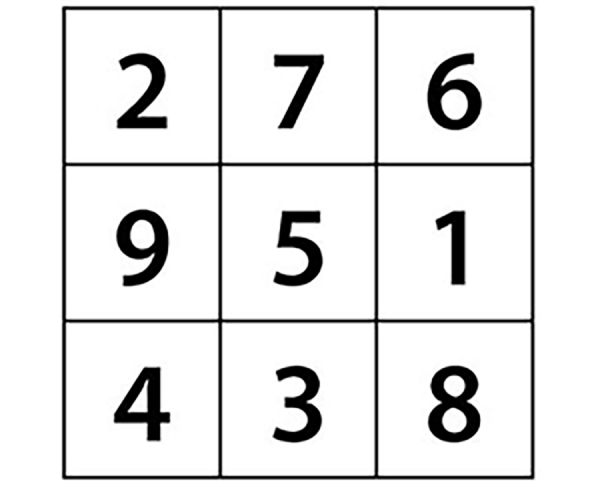
1’den 9’a kadar olan sayıları sadece birer kez kullanarak, tüm satır ve sütunlar ile köşegenlerde bulunan sayıların toplamı eşit olacak şekilde 3x3’lük bir kare oluşturabilir misiniz?

Kendisinden ve 1’den başka böleni bulunmayan asal sayıların sonsuz olduğunu duymuşsunuzdur. Peki sonsuz tane asal sayı olduğunu nasıl biliyoruz?

2, 3, 5, 7, 11, … şeklinde devam eden, kendisinden ve 1’den başka pozitif böleni olmayan 2 ve 2’den büyük sayılara asal sayı dendiğini birçoğumuz biliyoruz. Peki, asal sayılar neden önemlidir? Günlük hayatta ne işimize yarar?

İsviçre’deki Graubünden Üniversitesinden bir grup araştırmacı, π sayısının ondalık değerini 62,8 trilyon basamağa kadar hesaplayarak dünya rekoru kırdı.

Fermat’nın son teoremi: Eğer n >2 bir tam sayı ise xⁿ+yⁿ=zⁿ denkleminin pozitif x, y, z tam sayıları için çözümü yoktur. 

Matematikle ilgili yeni bir video ile karşınızdayız! Bu videoda bilinen ilk irrasyonel sayı olan karekök iki sayısının nasıl keşfedildiğini anlatıyoruz.

Eski çağlarda insanlar avladıkları veya sürülerinde bulunan hayvanların sayısını belirlemek için sayılara ihtiyaç duyarlardı. Bu ihtiyaçlarını mağara duvarlarına çizgi çekerek veya ipe düğüm atarak karşıladılar. İlerleyen süreçte önce sayılar keşfedildi. Daha sonra ise belirli miktarları daha küçük parçalara bölmek için kullanılan kesirler yani rasyonel sayılar ortaya çıktı. Milattan önce beşinci yüzyılda yaşayan Antik Yunan filozofu Pisagor ve arkadaşları, tüm sayıları sayma sayıları veya iki sayının birbirine oranı olarak düşünüyorlardı. Yani tüm sayıları rasyonel sayılardan ibaret sanıyorlardı. Fakat Pisagor’un öğrencisi Hippasus, kenar uzunlukları bir birim olan bir dik üçgende hipotenüsün uzunluğunun kök iki birim olduğunu ve bu sayının rasyonel bir sayı olmadığını iddia etti. Peki Hippasus bunu neye dayanarak söylemişti?

Fibonacci dizisi bir sayı dizisidir ve {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …}  şeklinde devam eden sonsuz sayılardan oluşur.

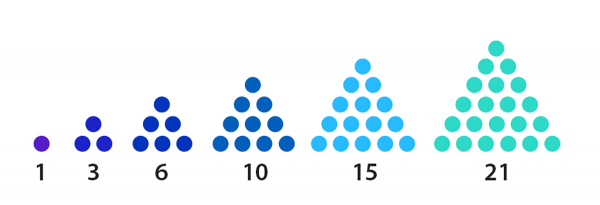
1’den n ’ye kadar olan ardışık n tane doğal sayının toplamı şeklinde yazılabilen sayılara “üçgensel sayı” denir.

Matematikte bazı pozitif tam sayıların pozitif bölenleri toplamı, sayının kendisinin iki katına eşittir. Bu tür sayılara “mükemmel sayı” denir.